Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Post-Pruning von Entscheidungsbäumen mit Kostenkomplexitäts-Pruning#
Der DecisionTreeClassifier bietet Parameter wie min_samples_leaf und max_depth, um zu verhindern, dass ein Baum überangepasst wird. Kostenkomplexitäts-Pruning bietet eine weitere Option zur Kontrolle der Größe eines Baumes. Im DecisionTreeClassifier wird diese Pruning-Technik durch den Kostenkomplexitäts-Parameter ccp_alpha parametrisiert. Größere Werte von ccp_alpha erhöhen die Anzahl der beschnittenen Knoten. Hier zeigen wir nur die Auswirkung von ccp_alpha auf die Regularisierung der Bäume und wie man ein ccp_alpha basierend auf Validierungs-Scores auswählt.
Siehe auch Minimales Kostenkomplexitäts-Pruning für Details zum Pruning.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
Gesamte Unreinheit von Blättern vs. effektive Alphas des beschnittenen Baumes#
Minimales Kostenkomplexitäts-Pruning findet rekursiv den Knoten mit der „schwächsten Verbindung“. Die schwächste Verbindung wird durch einen effektiven Alpha-Wert charakterisiert, wobei zuerst die Knoten mit dem kleinsten effektiven Alpha-Wert beschnitten werden. Um eine Vorstellung davon zu bekommen, welche Werte von ccp_alpha geeignet sein könnten, stellt scikit-learn DecisionTreeClassifier.cost_complexity_pruning_path zur Verfügung, die die effektiven Alphas und die entsprechenden gesamten Blattunreinheiten in jedem Schritt des Pruning-Prozesses zurückgibt. Wenn Alpha zunimmt, wird mehr vom Baum beschnitten, was die Gesamtunreinheit seiner Blätter erhöht.
X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities
In der folgenden Grafik wird der maximale effektive Alpha-Wert entfernt, da es sich um den trivialen Baum mit nur einem Knoten handelt.
fig, ax = plt.subplots()
ax.plot(ccp_alphas[:-1], impurities[:-1], marker="o", drawstyle="steps-post")
ax.set_xlabel("effective alpha")
ax.set_ylabel("total impurity of leaves")
ax.set_title("Total Impurity vs effective alpha for training set")
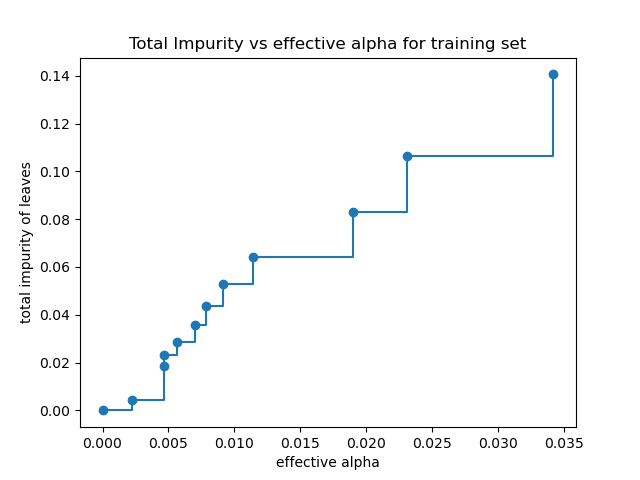
Text(0.5, 1.0, 'Total Impurity vs effective alpha for training set')
Als Nächstes trainieren wir einen Entscheidungsbaum unter Verwendung der effektiven Alphas. Der letzte Wert in ccp_alphas ist der Alpha-Wert, der den gesamten Baum beschnitten lässt, wobei der Baum, clfs[-1], mit einem Knoten zurückbleibt.
clfs = []
for ccp_alpha in ccp_alphas:
clf = DecisionTreeClassifier(random_state=0, ccp_alpha=ccp_alpha)
clf.fit(X_train, y_train)
clfs.append(clf)
print(
"Number of nodes in the last tree is: {} with ccp_alpha: {}".format(
clfs[-1].tree_.node_count, ccp_alphas[-1]
)
)
Number of nodes in the last tree is: 1 with ccp_alpha: 0.3272984419327777
Für den Rest dieses Beispiels entfernen wir das letzte Element in clfs und ccp_alphas, da es sich um den trivialen Baum mit nur einem Knoten handelt. Hier zeigen wir, dass die Anzahl der Knoten und die Baumtiefe mit zunehmendem Alpha abnehmen.
clfs = clfs[:-1]
ccp_alphas = ccp_alphas[:-1]
node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
fig, ax = plt.subplots(2, 1)
ax[0].plot(ccp_alphas, node_counts, marker="o", drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[0].set_title("Number of nodes vs alpha")
ax[1].plot(ccp_alphas, depth, marker="o", drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[1].set_title("Depth vs alpha")
fig.tight_layout()
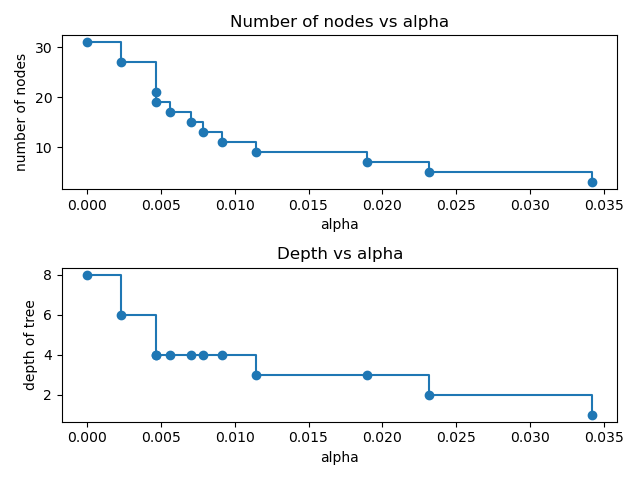
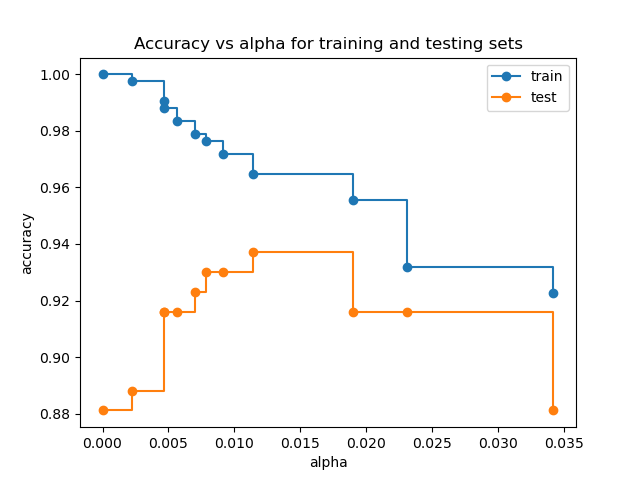
Genauigkeit vs. Alpha für Trainings- und Testdatensätze#
Wenn ccp_alpha auf Null gesetzt wird und die anderen Standardparameter des DecisionTreeClassifier beibehalten werden, überanpasst sich der Baum, was zu einer Trainingsgenauigkeit von 100 % und einer Testgenauigkeit von 88 % führt. Mit zunehmendem Alpha wird mehr vom Baum beschnitten, wodurch ein Entscheidungsbaum erstellt wird, der besser generalisiert. In diesem Beispiel maximiert die Einstellung von ccp_alpha=0.015 die Testgenauigkeit.
train_scores = [clf.score(X_train, y_train) for clf in clfs]
test_scores = [clf.score(X_test, y_test) for clf in clfs]
fig, ax = plt.subplots()
ax.set_xlabel("alpha")
ax.set_ylabel("accuracy")
ax.set_title("Accuracy vs alpha for training and testing sets")
ax.plot(ccp_alphas, train_scores, marker="o", label="train", drawstyle="steps-post")
ax.plot(ccp_alphas, test_scores, marker="o", label="test", drawstyle="steps-post")
ax.legend()
plt.show()
Gesamte Laufzeit des Skripts: (0 Minuten 0,380 Sekunden)
Verwandte Beispiele
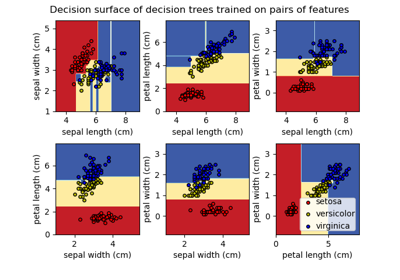
Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten
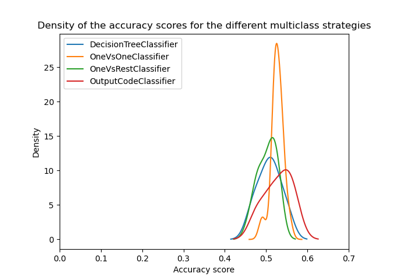
Übersicht über Multiklassen-Training Meta-Estimator