Wahrscheinlichkeitskalibrierung von Klassifikatoren

Bei der Durchführung von Klassifizierungen möchten Sie oft nicht nur die Klassenbezeichnung, sondern auch die zugehörige Wahrscheinlichkeit vorhersagen. Diese Wahrscheinlichkeit gibt Ihnen eine Art Vertrauen in die Vorhersage. Allerdings liefern nicht alle Klassifikatoren gut kalibrierte Wahrscheinlichkeiten, einige sind zu selbstbewusst, während andere zu wenig selbstbewusst sind. Daher ist eine separate Kalibrierung der vorhergesagten Wahrscheinlichkeiten als Nachbearbeitung oft wünschenswert. Dieses Beispiel veranschaulicht zwei verschiedene Methoden für diese Kalibrierung und bewertet die Qualität der zurückgegebenen Wahrscheinlichkeiten anhand des Brier-Scores (siehe https://en.wikipedia.org/wiki/Brier_score).

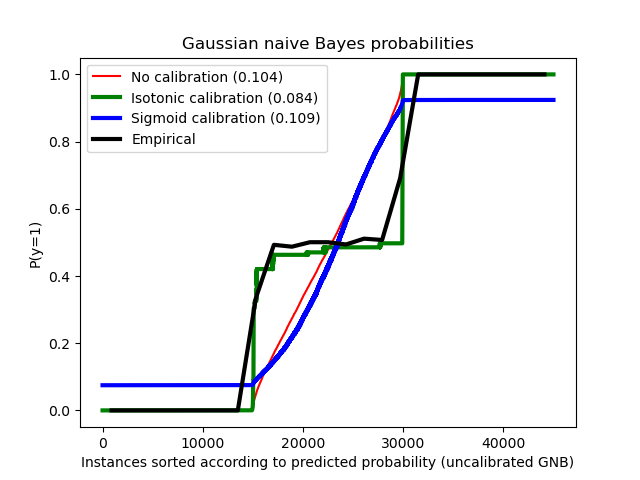
Verglichen werden die geschätzte Wahrscheinlichkeit mit einem Gaußschen Naive-Bayes-Klassifikator ohne Kalibrierung, mit einer Sigmoid-Kalibrierung und mit einer nichtparametrischen isotonen Kalibrierung. Man kann beobachten, dass nur das nichtparametrische Modell in der Lage ist, eine Wahrscheinlichkeitskalibrierung bereitzustellen, die für die meisten Stichproben, die zum mittleren Cluster mit heterogenen Labels gehören, Wahrscheinlichkeiten nahe dem erwarteten 0,5 liefert. Dies führt zu einem signifikant verbesserten Brier-Score.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Synthetischen Datensatz generieren

import numpy as np

from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split

n_samples = 50000

# Generate 3 blobs with 2 classes where the second blob contains
# half positive samples and half negative samples. Probability in this
# blob is therefore 0.5.
centers = [(-5, -5), (0, 0), (5, 5)]
X, y = make_blobs(n_samples=n_samples, centers=centers, shuffle=False, random_state=42)

y[: n_samples // 2] = 0
y[n_samples // 2 :] = 1
sample_weight = np.random.RandomState(42).rand(y.shape[0])

# split train, test for calibration
X_train, X_test, y_train, y_test, sw_train, sw_test = train_test_split(
    X, y, sample_weight, test_size=0.9, random_state=42
)

Gaußscher Naive-Bayes

from sklearn.calibration import CalibratedClassifierCV
from sklearn.metrics import brier_score_loss
from sklearn.naive_bayes import GaussianNB

# With no calibration
clf = GaussianNB()
clf.fit(X_train, y_train)  # GaussianNB itself does not support sample-weights
prob_pos_clf = clf.predict_proba(X_test)[:, 1]

# With isotonic calibration
clf_isotonic = CalibratedClassifierCV(clf, cv=2, method="isotonic")
clf_isotonic.fit(X_train, y_train, sample_weight=sw_train)
prob_pos_isotonic = clf_isotonic.predict_proba(X_test)[:, 1]

# With sigmoid calibration
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method="sigmoid")
clf_sigmoid.fit(X_train, y_train, sample_weight=sw_train)
prob_pos_sigmoid = clf_sigmoid.predict_proba(X_test)[:, 1]

print("Brier score losses: (the smaller the better)")

clf_score = brier_score_loss(y_test, prob_pos_clf, sample_weight=sw_test)
print("No calibration: %1.3f" % clf_score)

clf_isotonic_score = brier_score_loss(y_test, prob_pos_isotonic, sample_weight=sw_test)
print("With isotonic calibration: %1.3f" % clf_isotonic_score)

clf_sigmoid_score = brier_score_loss(y_test, prob_pos_sigmoid, sample_weight=sw_test)
print("With sigmoid calibration: %1.3f" % clf_sigmoid_score)

Brier score losses: (the smaller the better)
No calibration: 0.104
With isotonic calibration: 0.084
With sigmoid calibration: 0.109

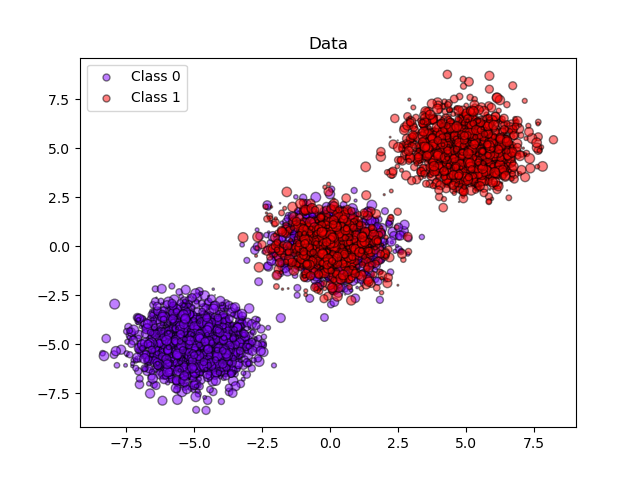
Daten und die vorhergesagten Wahrscheinlichkeiten plotten

import matplotlib.pyplot as plt
from matplotlib import cm

plt.figure()
y_unique = np.unique(y)
colors = cm.rainbow(np.linspace(0.0, 1.0, y_unique.size))
for this_y, color in zip(y_unique, colors):
    this_X = X_train[y_train == this_y]
    this_sw = sw_train[y_train == this_y]
    plt.scatter(
        this_X[:, 0],
        this_X[:, 1],
        s=this_sw * 50,
        c=color[np.newaxis, :],
        alpha=0.5,
        edgecolor="k",
        label="Class %s" % this_y,
    )
plt.legend(loc="best")
plt.title("Data")

plt.figure()

order = np.lexsort((prob_pos_clf,))
plt.plot(prob_pos_clf[order], "r", label="No calibration (%1.3f)" % clf_score)
plt.plot(
    prob_pos_isotonic[order],
    "g",
    linewidth=3,
    label="Isotonic calibration (%1.3f)" % clf_isotonic_score,
)
plt.plot(
    prob_pos_sigmoid[order],
    "b",
    linewidth=3,
    label="Sigmoid calibration (%1.3f)" % clf_sigmoid_score,
)
plt.plot(
    np.linspace(0, y_test.size, 51)[1::2],
    y_test[order].reshape(25, -1).mean(1),
    "k",
    linewidth=3,
    label=r"Empirical",
)
plt.ylim([-0.05, 1.05])
plt.xlabel("Instances sorted according to predicted probability (uncalibrated GNB)")
plt.ylabel("P(y=1)")
plt.legend(loc="upper left")
plt.title("Gaussian naive Bayes probabilities")

plt.show()

• 
• 

Verwandte Beispiele

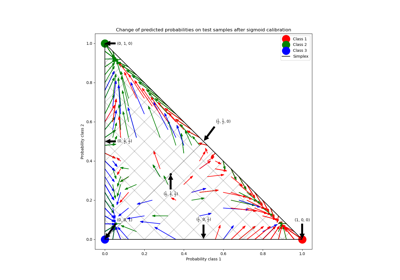
Wahrscheinlichkeitskalibrierungskurven

Wahrscheinlichkeitskalibrierungskurven

Vergleich der Kalibrierung von Klassifikatoren

Vergleich der Kalibrierung von Klassifikatoren

Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation

Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation

Beispiele für die Verwendung von FrozenEstimator

Beispiele für die Verwendung von FrozenEstimator