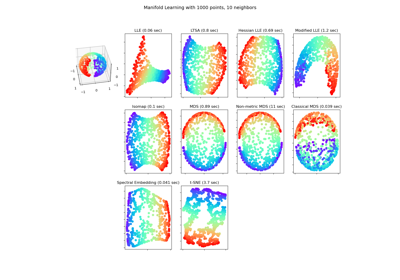
Vergleich von Manifold Learning-Methoden

Eine Illustration der Dimensionsreduktion auf dem S-Kurven-Datensatz mit verschiedenen Manifold Learning-Methoden.

Eine Diskussion und ein Vergleich dieser Algorithmen finden Sie auf der Seite des Manifold-Moduls

Ein ähnliches Beispiel, bei dem die Methoden auf einen Kugel-Datensatz angewendet werden, finden Sie unter Manifold Learning-Methoden auf einer durchtrennten Kugel

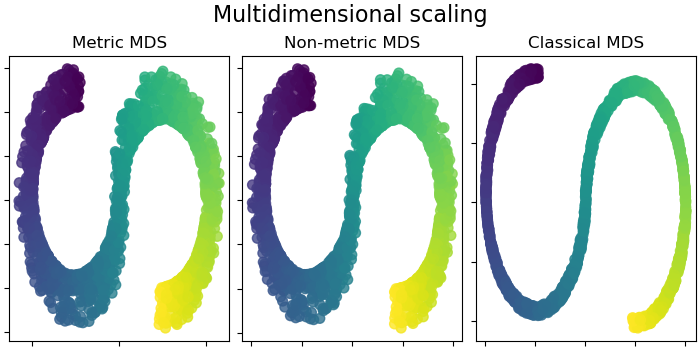
Beachten Sie, dass der Zweck von MDS darin besteht, eine niedrigdimensionale Darstellung der Daten (hier 2D) zu finden, in der die Abstände die Abstände im ursprünglichen hochdimensionalen Raum gut respektieren. Im Gegensatz zu anderen Manifold Learning-Algorithmen strebt es keine isotrope Darstellung der Daten im niedrigdimensionalen Raum an.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Dataset-Vorbereitung

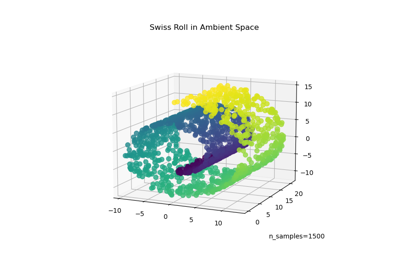
Wir beginnen mit der Generierung des S-Kurven-Datensatzes.

import matplotlib.pyplot as plt

# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d  # noqa: F401
from matplotlib import ticker

from sklearn import datasets, manifold

n_samples = 1500
S_points, S_color = datasets.make_s_curve(n_samples, random_state=0)

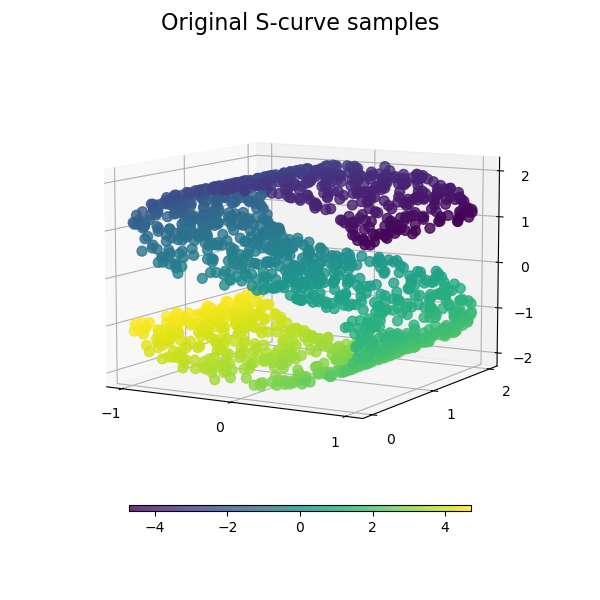
Betrachten wir die Originaldaten. Definieren wir auch einige Hilfsfunktionen, die wir später verwenden werden.

def plot_3d(points, points_color, title):
    x, y, z = points.T

    fig, ax = plt.subplots(
        figsize=(6, 6),
        facecolor="white",
        tight_layout=True,
        subplot_kw={"projection": "3d"},
    )
    fig.suptitle(title, size=16)
    col = ax.scatter(x, y, z, c=points_color, s=50, alpha=0.8)
    ax.view_init(azim=-60, elev=9)
    ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.zaxis.set_major_locator(ticker.MultipleLocator(1))

    fig.colorbar(col, ax=ax, orientation="horizontal", shrink=0.6, aspect=60, pad=0.01)
    plt.show()


def plot_2d(points, points_color, title):
    fig, ax = plt.subplots(figsize=(3, 3), facecolor="white", constrained_layout=True)
    fig.suptitle(title, size=16)
    add_2d_scatter(ax, points, points_color)
    plt.show()


def add_2d_scatter(ax, points, points_color, title=None):
    x, y = points.T
    ax.scatter(x, y, c=points_color, s=50, alpha=0.8)
    ax.set_title(title)
    ax.xaxis.set_major_formatter(ticker.NullFormatter())
    ax.yaxis.set_major_formatter(ticker.NullFormatter())


plot_3d(S_points, S_color, "Original S-curve samples")

Algorithmen für das Manifold Learning definieren

Manifold Learning ist ein Ansatz zur nichtlinearen Dimensionsreduktion. Algorithmen für diese Aufgabe basieren auf der Idee, dass die Dimensionalität vieler Datensätze nur künstlich hoch ist.

Lesen Sie mehr im Benutzerhandbuch.

n_neighbors = 12  # neighborhood which is used to recover the locally linear structure
n_components = 2  # number of coordinates for the manifold

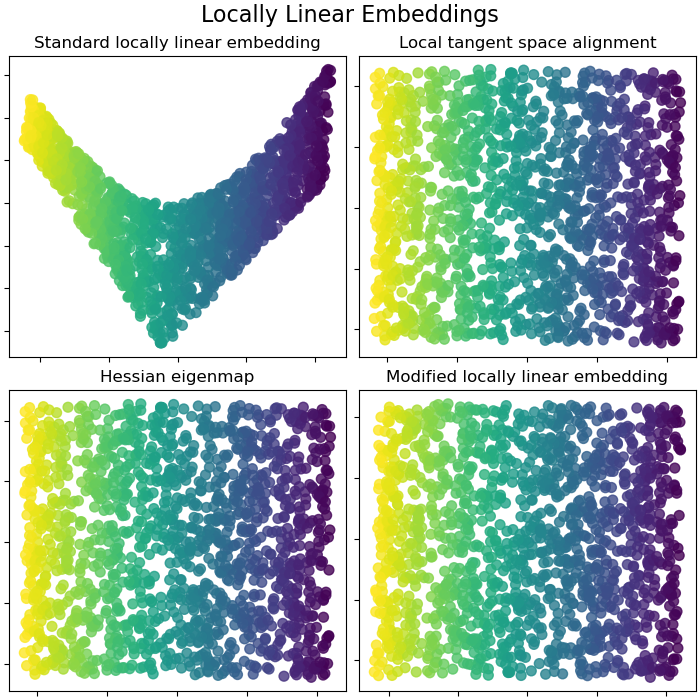
Locally Linear Embeddings

Locally linear embedding (LLE) kann als eine Reihe lokaler Hauptkomponentenanalysen betrachtet werden, die global verglichen werden, um die beste nichtlineare Einbettung zu finden. Lesen Sie mehr im Benutzerhandbuch.

params = {
    "n_neighbors": n_neighbors,
    "n_components": n_components,
    "eigen_solver": "auto",
    "random_state": 0,
}

lle_standard = manifold.LocallyLinearEmbedding(method="standard", **params)
S_standard = lle_standard.fit_transform(S_points)

lle_ltsa = manifold.LocallyLinearEmbedding(method="ltsa", **params)
S_ltsa = lle_ltsa.fit_transform(S_points)

lle_hessian = manifold.LocallyLinearEmbedding(method="hessian", **params)
S_hessian = lle_hessian.fit_transform(S_points)

lle_mod = manifold.LocallyLinearEmbedding(method="modified", **params)
S_mod = lle_mod.fit_transform(S_points)

fig, axs = plt.subplots(
    nrows=2, ncols=2, figsize=(7, 7), facecolor="white", constrained_layout=True
)
fig.suptitle("Locally Linear Embeddings", size=16)

lle_methods = [
    ("Standard locally linear embedding", S_standard),
    ("Local tangent space alignment", S_ltsa),
    ("Hessian eigenmap", S_hessian),
    ("Modified locally linear embedding", S_mod),
]
for ax, method in zip(axs.flat, lle_methods):
    name, points = method
    add_2d_scatter(ax, points, S_color, name)

plt.show()

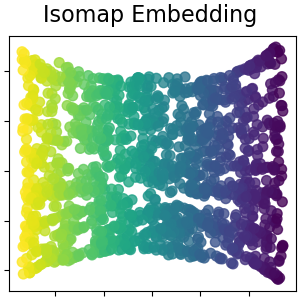
Isomap Embedding

Nichtlineare Dimensionsreduktion durch isometrische Abbildung. Isomap sucht eine niedrigdimensionale Einbettung, die die geodätischen Abstände zwischen allen Punkten beibehält. Lesen Sie mehr im Benutzerhandbuch.

isomap = manifold.Isomap(n_neighbors=n_neighbors, n_components=n_components, p=1)
S_isomap = isomap.fit_transform(S_points)

plot_2d(S_isomap, S_color, "Isomap Embedding")

Multidimensionale Skalierung

Multidimensionale Skalierung (MDS) sucht eine niedrigdimensionale Darstellung der Daten, in der die Abstände die Abstände im ursprünglichen hochdimensionalen Raum gut respektieren. Lesen Sie mehr im Benutzerhandbuch.

md_scaling = manifold.MDS(
    n_components=n_components,
    max_iter=50,
    n_init=1,
    random_state=0,
    init="classical_mds",
    normalized_stress=False,
)
S_scaling_metric = md_scaling.fit_transform(S_points)

md_scaling_nonmetric = manifold.MDS(
    n_components=n_components,
    max_iter=50,
    n_init=1,
    random_state=0,
    normalized_stress=False,
    metric_mds=False,
    init="classical_mds",
)
S_scaling_nonmetric = md_scaling_nonmetric.fit_transform(S_points)

md_scaling_classical = manifold.ClassicalMDS(n_components=n_components)
S_scaling_classical = md_scaling_classical.fit_transform(S_points)

fig, axs = plt.subplots(
    nrows=1, ncols=3, figsize=(7, 3.5), facecolor="white", constrained_layout=True
)
fig.suptitle("Multidimensional scaling", size=16)

mds_methods = [
    ("Metric MDS", S_scaling_metric),
    ("Non-metric MDS", S_scaling_nonmetric),
    ("Classical MDS", S_scaling_classical),
]
for ax, method in zip(axs.flat, mds_methods):
    name, points = method
    add_2d_scatter(ax, points, S_color, name)

plt.show()

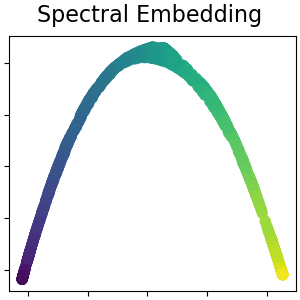
Spektrale Einbettung für nichtlineare Dimensionsreduktion

Diese Implementierung verwendet Laplacian Eigenmaps, die eine niedrigdimensionale Darstellung der Daten durch eine spektrale Zerlegung des Graphen-Laplacians findet. Lesen Sie mehr im Benutzerhandbuch.

spectral = manifold.SpectralEmbedding(
    n_components=n_components, n_neighbors=n_neighbors, random_state=42
)
S_spectral = spectral.fit_transform(S_points)

plot_2d(S_spectral, S_color, "Spectral Embedding")

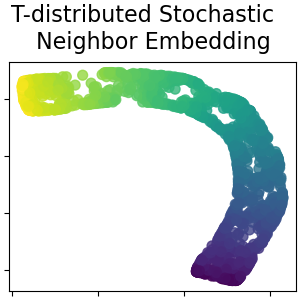
T-verteilte stochastische Nachbareinbettung

Sie wandelt Ähnlichkeiten zwischen Datenpunkten in gemeinsame Wahrscheinlichkeiten um und versucht, die Kullback-Leibler-Divergenz zwischen den gemeinsamen Wahrscheinlichkeiten der niedrigdimensionalen Einbettung und den hochdimensionalen Daten zu minimieren. t-SNE hat eine Kostenfunktion, die nicht konvex ist, d.h. mit unterschiedlichen Initialisierungen können unterschiedliche Ergebnisse erzielt werden. Lesen Sie mehr im Benutzerhandbuch.

t_sne = manifold.TSNE(
    n_components=n_components,
    perplexity=30,
    init="random",
    max_iter=250,
    random_state=0,
)
S_t_sne = t_sne.fit_transform(S_points)

plot_2d(S_t_sne, S_color, "T-distributed Stochastic  \n Neighbor Embedding")

Verwandte Beispiele

Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

Mannigfaltigkeitslernen auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap...

Manifold Learning Methoden auf einer abgetrennten Sphäre

Manifold Learning Methoden auf einer abgetrennten Sphäre

Visualisierung der Aktienmarktstruktur

Visualisierung der Aktienmarktstruktur

Swiss Roll und Swiss-Hole Reduktion

Swiss Roll und Swiss-Hole Reduktion