2.2. Mannigfaltigkeitslernen

Suchen Sie nach den bloßen Notwendigkeiten

Die einfachen, bloßen Notwendigkeiten

Vergessen Sie Ihre Sorgen und Ihren Streit

Ich meine die bloßen Notwendigkeiten

Rezepte von Mutter Natur

Die die bloßen Notwendigkeiten des Lebens bringen

– Baloo’s Lied [Das Dschungelbuch]

Mannigfaltigkeitslernen ist ein Ansatz zur nichtlinearen Dimensionsreduktion. Algorithmen für diese Aufgabe basieren auf der Idee, dass die Dimensionalität vieler Datensätze nur künstlich hoch ist.

2.2.1. Einleitung

Hochdimensionale Datensätze können sehr schwer zu visualisieren sein. Während Daten in zwei oder drei Dimensionen geplottet werden können, um die inhärente Struktur der Daten zu zeigen, sind äquivalente hochdimensionale Plots viel weniger intuitiv. Um die Struktur eines Datensatzes zu visualisieren, muss die Dimension auf irgendeine Weise reduziert werden.

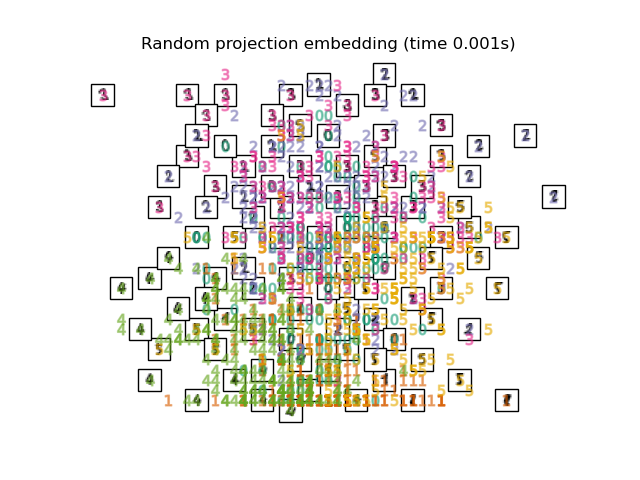
Der einfachste Weg, diese Dimensionsreduktion zu erreichen, ist die zufällige Projektion der Daten. Obwohl dies ein gewisses Maß an Visualisierung der Datenstruktur ermöglicht, lässt die Zufälligkeit der Wahl viel zu wünschen übrig. Bei einer zufälligen Projektion ist es wahrscheinlich, dass die interessantere Struktur innerhalb der Daten verloren geht.

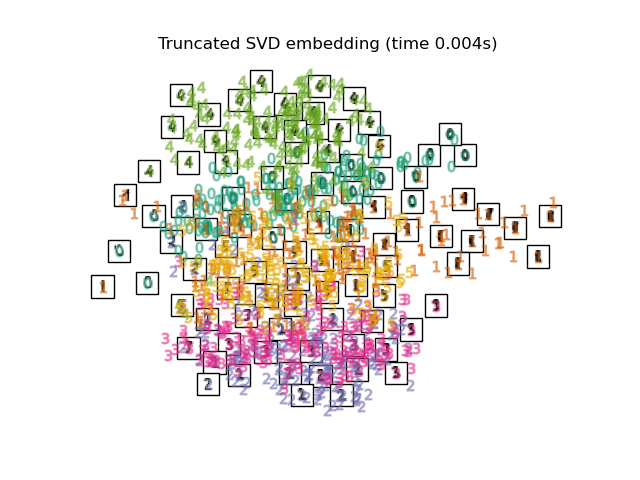
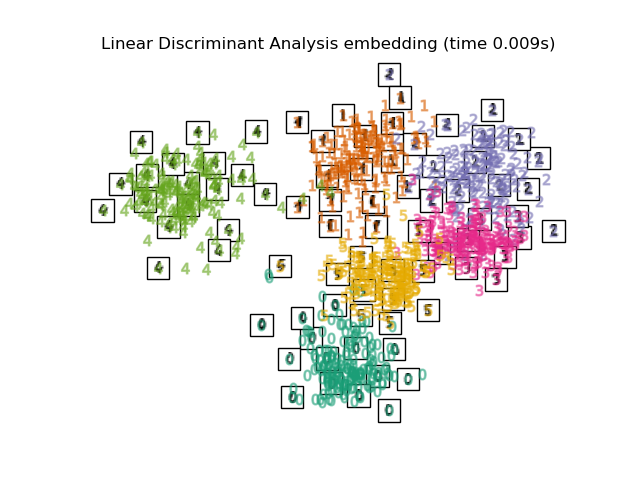
Um dieses Problem anzugehen, wurden eine Reihe von überwachten und unüberwachten linearen Dimensionsreduktionsframeworks entwickelt, wie z. B. Hauptkomponentenanalyse (PCA), unabhängige Komponentenanalyse, lineare Diskriminanzanalyse und andere. Diese Algorithmen definieren spezifische Kriterien, um eine "interessante" lineare Projektion der Daten auszuwählen. Diese Methoden können leistungsfähig sein, verpassen aber oft wichtige nichtlineare Strukturen in den Daten.

Mannigfaltigkeitslernen kann als Versuch betrachtet werden, lineare Frameworks wie PCA zu verallgemeinern, um für nichtlineare Strukturen in Daten empfindlich zu sein. Obwohl überwachte Varianten existieren, ist das typische Mannigfaltigkeitslernen unüberwacht: Es lernt die hochdimensionale Struktur der Daten aus den Daten selbst, ohne vordefinierte Klassifikationen zu verwenden.

Beispiele

• Siehe Mannigfaltigkeitslernen bei handgeschriebenen Ziffern: Locally Linear Embedding, Isomap… für ein Beispiel der Dimensionsreduktion bei handgeschriebenen Ziffern.

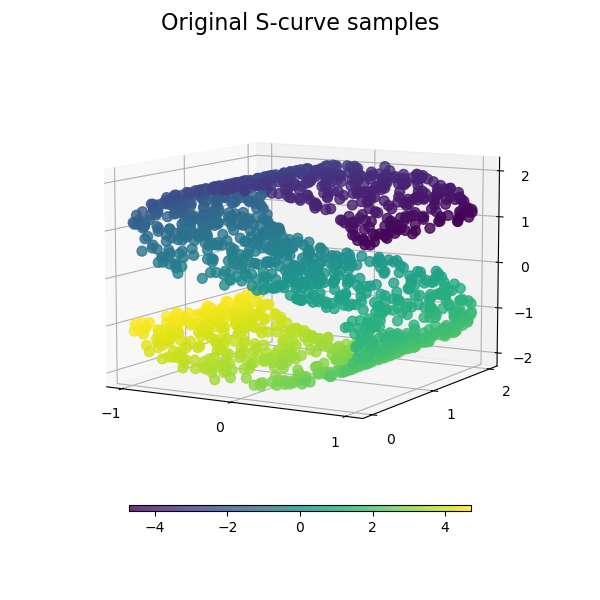
• Siehe Vergleich von Mannigfaltigkeitslernen-Methoden für ein Beispiel der Dimensionsreduktion auf einem "S-Kurven"-Toy-Datensatz.

• Siehe Visualisierung der Aktienmarktstruktur für ein Beispiel der Verwendung von Mannigfaltigkeitslernen zur Abbildung der Aktienmarktstruktur basierend auf historischen Aktienkursen.

• Siehe Mannigfaltigkeitslernen-Methoden auf einer abgeschnittenen Kugel für ein Beispiel von Mannigfaltigkeitslernen-Techniken, die auf einen sphärischen Datensatz angewendet werden.

• Siehe Reduzierung von Schweizer Rolle und Schweizer Loch für ein Beispiel der Verwendung von Mannigfaltigkeitslernen-Techniken auf einem Schweizer Rollen-Datensatz.

Die in scikit-learn verfügbaren Implementierungen des Mannigfaltigkeitslernens werden unten zusammengefasst

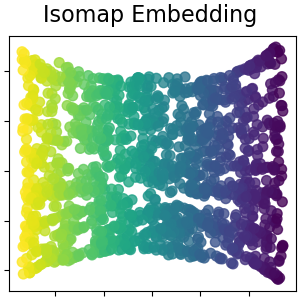
2.2.2. Isomap

Einer der frühesten Ansätze zum Mannigfaltigkeitslernen ist der Isomap-Algorithmus, kurz für Isometric Mapping. Isomap kann als Erweiterung von Multi-dimensional Scaling (MDS) oder Kernel PCA betrachtet werden. Isomap sucht nach einer niedrigdimensionalen Einbettung, die die geodätischen Abstände zwischen allen Punkten beibehält. Isomap kann mit dem Objekt Isomap durchgeführt werden.

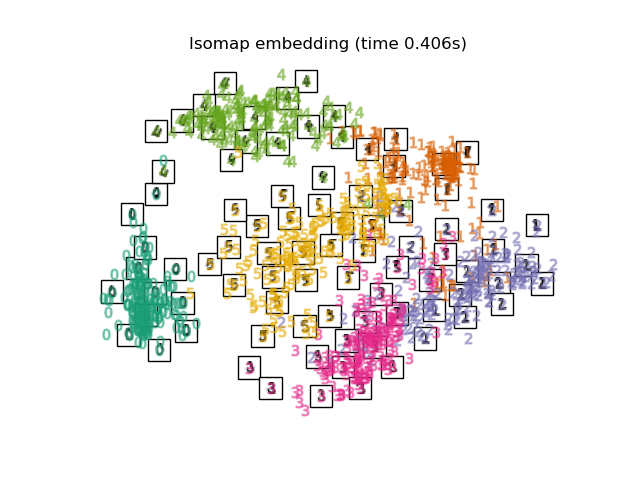
Komplexität

Der Isomap-Algorithmus umfasst drei Schritte

1. Suche nach nächsten Nachbarn. Isomap verwendet BallTree für eine effiziente Nachbarschaftssuche. Die Kosten betragen ungefähr \(O[D \log(k) N \log(N)]\) für \(k\) nächste Nachbarn von \(N\) Punkten in \(D\) Dimensionen.

2. Suche nach dem kürzesten Pfad im Graphen. Die effizientesten bekannten Algorithmen hierfür sind der Dijkstra-Algorithmus mit Kosten von ca. \(O[N^2(k + \log(N))]\) oder der Floyd-Warshall-Algorithmus mit Kosten von \(O[N^3]\). Der Algorithmus kann vom Benutzer mit dem Schlüsselwort path_method von Isomap ausgewählt werden. Wenn nicht spezifiziert, versucht der Code, den besten Algorithmus für die Eingabedaten auszuwählen.

3. Partielle Eigenwertzerlegung. Die Einbettung wird in den Eigenvektoren kodiert, die den \(d\) größten Eigenwerten des \(N \times N\) Isomap-Kernels entsprechen. Für einen dichten Löser betragen die Kosten ca. \(O[d N^2]\). Diese Kosten können oft durch die Verwendung des ARPACK-Lösers verbessert werden. Der Eigenwertlöser kann vom Benutzer mit dem Schlüsselwort eigen_solver von Isomap spezifiziert werden. Wenn nicht spezifiziert, versucht der Code, den besten Algorithmus für die Eingabedaten auszuwählen.

Die Gesamtkomplexität von Isomap beträgt \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „A global geometric framework for nonlinear dimensionality reduction“ Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

2.2.3. Locally Linear Embedding

Locally Linear Embedding (LLE) sucht nach einer niedrigdimensionalen Projektion der Daten, die Abstände innerhalb lokaler Nachbarschaften beibehält. Es kann als eine Reihe lokaler Hauptkomponentenanalysen betrachtet werden, die global verglichen werden, um die beste nichtlineare Einbettung zu finden.

Locally Linear Embedding kann mit der Funktion locally_linear_embedding oder seinem objektorientierten Gegenstück LocallyLinearEmbedding durchgeführt werden.

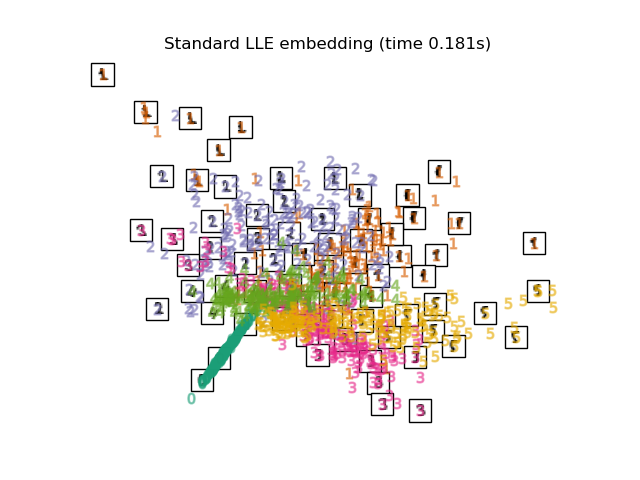
Komplexität

Der Standard-LLE-Algorithmus umfasst drei Schritte

1. Suche nach nächsten Nachbarn. Siehe Diskussion unter Isomap oben.

2. Konstruktion der Gewichtsmatrix. \(O[D N k^3]\). Die Konstruktion der LLE-Gewichtsmatrix beinhaltet die Lösung einer \(k \times k\)-linearen Gleichung für jede der \(N\) lokalen Nachbarschaften.

3. Partielle Eigenwertzerlegung. Siehe Diskussion unter Isomap oben.

Die Gesamtkomplexität des Standard-LLE beträgt \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „Nonlinear dimensionality reduction by locally linear embedding“ Roweis, S. & Saul, L. Science 290:2323 (2000)

2.2.4. Modifiziertes Locally Linear Embedding

Ein bekanntes Problem bei LLE ist das Regularisierungsproblem. Wenn die Anzahl der Nachbarn größer ist als die Anzahl der Eingabedimensionen, ist die Matrix, die jede lokale Nachbarschaft definiert, Rang-defizient. Um dies zu beheben, wendet das Standard-LLE einen willkürlichen Regularisierungsparameter \(r\) an, der sich relativ zur Spur der lokalen Gewichtsmatrix verhält. Obwohl formal gezeigt werden kann, dass die Lösung mit \(r \to 0\) zur gewünschten Einbettung konvergiert, gibt es keine Garantie dafür, dass die optimale Lösung für \(r > 0\) gefunden wird. Dieses Problem äußert sich in Einbettungen, die die zugrundeliegende Geometrie der Mannigfaltigkeit verzerren.

Eine Methode zur Behebung des Regularisierungsproblems ist die Verwendung mehrerer Gewichtsvektoren in jeder Nachbarschaft. Dies ist das Wesen des modifizierten Locally Linear Embedding (MLLE). MLLE kann mit der Funktion locally_linear_embedding oder seinem objektorientierten Gegenstück LocallyLinearEmbedding mit dem Schlüsselwort method = 'modified' durchgeführt werden. Es erfordert n_neighbors > n_components.

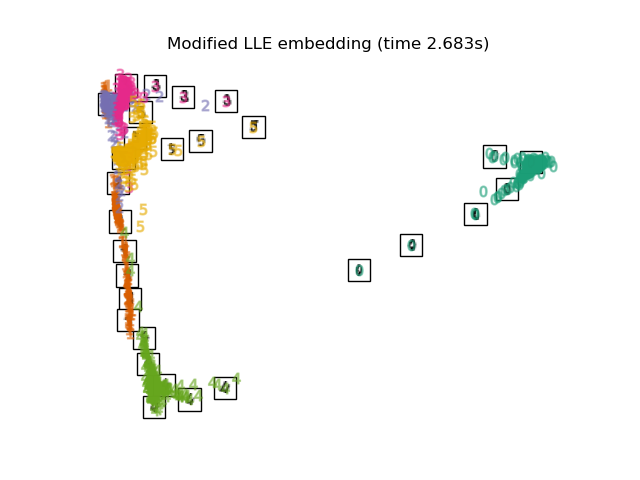
Komplexität

Der MLLE-Algorithmus umfasst drei Schritte

1. Suche nach nächsten Nachbarn. Wie beim Standard-LLE.

2. Konstruktion der Gewichtsmatrix. Ungefähr \(O[D N k^3] + O[N (k-D) k^2]\). Der erste Term ist exakt äquivalent zu dem des Standard-LLE. Der zweite Term bezieht sich auf die Konstruktion der Gewichtsmatrix aus mehreren Gewichten. In der Praxis sind die zusätzlichen Kosten für die Konstruktion der MLLE-Gewichtsmatrix relativ gering im Vergleich zu den Kosten der Schritte 1 und 3.

3. Partielle Eigenwertzerlegung. Wie beim Standard-LLE.

Die Gesamtkomplexität von MLLE beträgt \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „MLLE: Modified Locally Linear Embedding Using Multiple Weights“ Zhang, Z. & Wang, J.

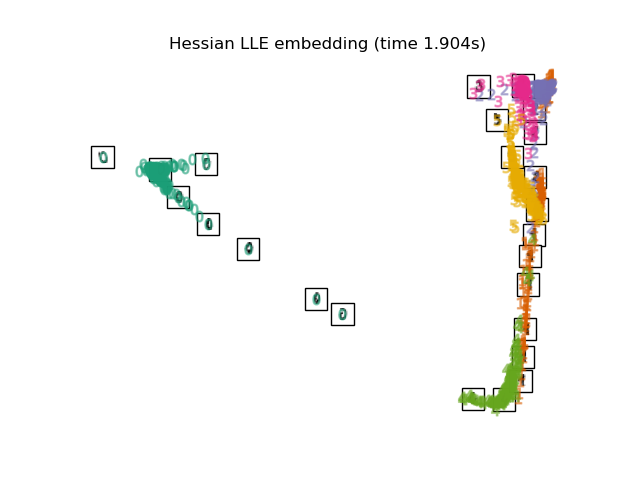
2.2.5. Hessian Eigenmapping

Hessian Eigenmapping (auch bekannt als Hessian-basierte LLE: HLLE) ist eine weitere Methode zur Lösung des Regularisierungsproblems von LLE. Sie beruht auf einer hessianbasierten quadratischen Form in jeder Nachbarschaft, die zur Wiederherstellung der lokal linearen Struktur verwendet wird. Obwohl andere Implementierungen eine schlechte Skalierbarkeit mit der Datengröße aufweisen, implementiert sklearn einige algorithmische Verbesserungen, die seine Kosten für kleine Ausgabedimensionen mit denen anderer LLE-Varianten vergleichbar machen. HLLE kann mit der Funktion locally_linear_embedding oder seinem objektorientierten Gegenstück LocallyLinearEmbedding mit dem Schlüsselwort method = 'hessian' durchgeführt werden. Es erfordert n_neighbors > n_components * (n_components + 3) / 2.

Komplexität

Der HLLE-Algorithmus umfasst drei Schritte

1. Suche nach nächsten Nachbarn. Wie beim Standard-LLE.

2. Konstruktion der Gewichtsmatrix. Ungefähr \(O[D N k^3] + O[N d^6]\). Der erste Term spiegelt Kosten wider, die denen des Standard-LLE ähneln. Der zweite Term stammt aus einer QR-Zerlegung des lokalen Hessian-Schätzers.

3. Partielle Eigenwertzerlegung. Wie beim Standard-LLE.

Die Gesamtkomplexität des Standard-HLLE beträgt \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data“ Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

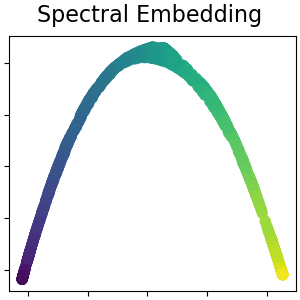
2.2.6. Spektrale Einbettung

Spektrale Einbettung ist ein Ansatz zur Berechnung einer nichtlinearen Einbettung. Scikit-learn implementiert Laplacian Eigenmaps, das eine niedrigdimensionale Darstellung der Daten mittels spektraler Zerlegung des Graphen-Laplacians findet. Der erzeugte Graph kann als diskrete Annäherung an die niedrigdimensionale Mannigfaltigkeit im hochdimensionalen Raum betrachtet werden. Die Minimierung einer kostenbasierten Funktion des Graphen stellt sicher, dass Punkte, die auf der Mannigfaltigkeit nahe beieinander liegen, auch in niedrigdimensionalen Raum nahe beieinander abgebildet werden, wodurch lokale Abstände erhalten bleiben. Spektrale Einbettung kann mit der Funktion spectral_embedding oder seinem objektorientierten Gegenstück SpectralEmbedding durchgeführt werden.

Komplexität

Der Algorithmus für spektrale Einbettung (Laplacian Eigenmaps) umfasst drei Schritte

1. Konstruktion eines gewichteten Graphen. Transformation der rohen Eingabedaten in eine Graphendarstellung mithilfe einer Affinitäts-(Adjazenz-)Matrix.

2. Konstruktion des Graphen-Laplacians. Der unnormalisierte Graphen-Laplacian wird als \(L = D - A\) konstruiert, und der normalisierte als \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).

3. Partielle Eigenwertzerlegung. Die Eigenwertzerlegung wird am Graphen-Laplacian durchgeführt.

Die Gesamtkomplexität der spektralen Einbettung beträgt \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „Laplacian Eigenmaps for Dimensionality Reduction and Data Representation“ M. Belkin, P. Niyogi, Neural Computation, Juni 2003; 15 (6):1373-1396.

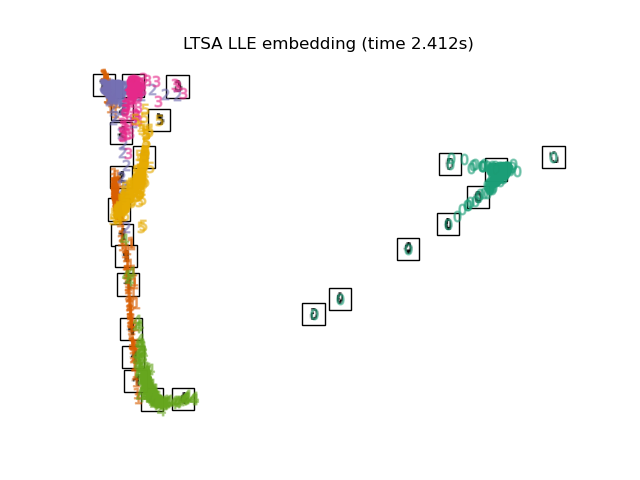
2.2.7. Local Tangent Space Alignment

Obwohl es sich technisch nicht um eine Variante von LLE handelt, ist Local Tangent Space Alignment (LTSA) algorithmisch LLE ähnlich genug, um in diese Kategorie eingeordnet zu werden. Anstatt sich auf die Beibehaltung von Nachbarschaftsabständen wie bei LLE zu konzentrieren, versucht LTSA, die lokale Geometrie jeder Nachbarschaft über ihren Tangentialraum zu charakterisieren und führt eine globale Optimierung durch, um diese lokalen Tangentialräume auszurichten und die Einbettung zu lernen. LTSA kann mit der Funktion locally_linear_embedding oder seinem objektorientierten Gegenstück LocallyLinearEmbedding mit dem Schlüsselwort method = 'ltsa' durchgeführt werden.

Komplexität

Der LTSA-Algorithmus umfasst drei Schritte

1. Suche nach nächsten Nachbarn. Wie beim Standard-LLE.

2. Konstruktion der Gewichtsmatrix. Ungefähr \(O[D N k^3] + O[k^2 d]\). Der erste Term spiegelt Kosten wider, die denen des Standard-LLE ähneln.

3. Partielle Eigenwertzerlegung. Wie beim Standard-LLE.

Die Gesamtkomplexität des Standard-LTSA beträgt \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).

• \(N\) : Anzahl der Trainingsdatenpunkte

• \(D\) : Eingabedimension

• \(k\) : Anzahl der nächsten Nachbarn

• \(d\) : Ausgabedimension

Referenzen

• „Principal manifolds and nonlinear dimensionality reduction via tangent space alignment“ Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

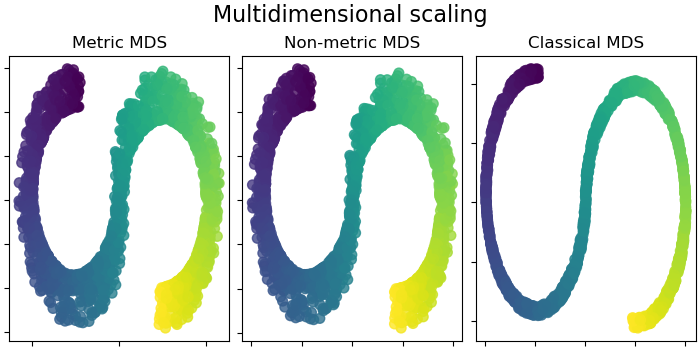
2.2.8. Multidimensionale Skalierung (MDS)

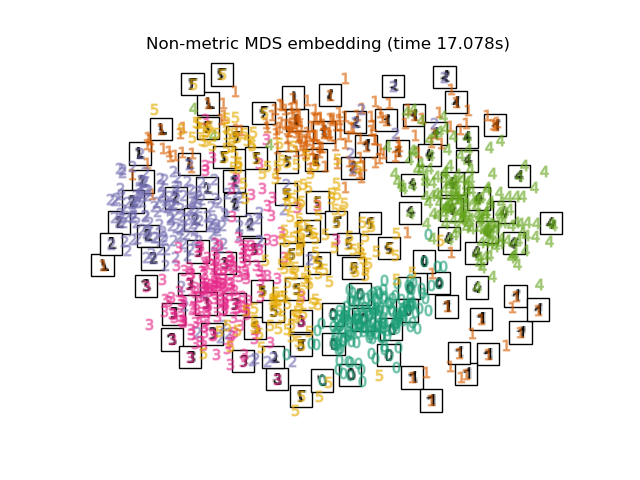
Multidimensionale Skalierung (MDS und ClassicalMDS) sucht nach einer niedrigdimensionalen Darstellung der Daten, in der die Abstände die Abstände im ursprünglichen hochdimensionalen Raum annähern.

Im Allgemeinen ist MDS eine Technik zur Analyse von Dissimilaritätsdaten. Sie versucht, Dissimiliaritäten als Abstände in einem euklidischen Raum zu modellieren. Die Daten können Bewertungen der Dissimilarität zwischen Objekten, Interaktionsfrequenzen von Molekülen oder Handelsindizes zwischen Ländern sein.

Es existieren drei Arten von MDS-Algorithmen: metrisch, nicht-metrisch und klassisch. In scikit-learn implementiert die Klasse MDS metrische und nicht-metrische MDS, während ClassicalMDS klassische MDS implementiert. Bei metrischem MDS werden die Abstände im Einbettungsraum so nah wie möglich an die Dissimiliaritätsdaten angenähert. Bei der nicht-metrischen Version versucht der Algorithmus, die Reihenfolge der Abstände beizubehalten, und sucht daher nach einer monotonen Beziehung zwischen den Abständen im eingebetteten Raum und den Eingabe-Dissimiliaritäten. Schließlich ist klassische MDS nah an PCA und approximiert anstelle von Abständen paarweise Skalarprodukte, was ein einfacheres Optimierungsproblem mit einer analytischen Lösung in Form einer Eigenwertzerlegung ist.

Sei \(\delta_{ij}\) die Dissimilaritätsmatrix zwischen den \(n\) Eingabepunkten (möglicherweise aus einigen paarweisen Abständen \(d_{ij}(X)\) zwischen den Koordinaten \(X\) der Eingabepunkte). Disparitäten \(\hat{d}_{ij} = f(\delta_{ij})\) sind eine Transformation der Dissimiliaritäten. Das MDS-Ziel, genannt roher Stress, ist dann definiert als \(\sum_{i < j} (\hat{d}_{ij} - d_{ij}(Z))^2\), wobei \(d_{ij}(Z)\) die paarweisen Abstände zwischen den Koordinaten \(Z\) der eingebetteten Punkte sind.

Metrische MDS

Im metrischen MDS-Modell (manchmal auch als Absolute MDS bezeichnet) sind die Disparitäten einfach gleich den Eingabe-Dissimiliaritäten \(\hat{d}_{ij} = \delta_{ij}\).

Nicht-metrische MDS

Nicht-metrische MDS konzentriert sich auf die Ordination der Daten. Wenn \(\delta_{ij} > \delta_{kl}\) ist, dann versucht die Einbettung, \(d_{ij}(Z) > d_{kl}(Z)\) durchzusetzen. Ein einfacher Algorithmus zur Durchsetzung der richtigen Ordination ist die Verwendung einer isotonischen Regression von \(d_{ij}(Z)\) auf \(\delta_{ij}\), was zu Disparitäten \(\hat{d}_{ij}\) führt, die eine monotone Transformation der Dissimiliaritäten \(\delta_{ij}\) sind und somit die gleiche Reihenfolge aufweisen. Dies geschieht wiederholt nach jedem Schritt des Optimierungsalgorithmus. Um die triviale Lösung zu vermeiden, bei der alle Einbettungspunkte übereinander liegen, werden die Disparitäten \(\hat{d}_{ij}\) normalisiert.

Beachten Sie, dass unser Ziel, da wir nur an der relativen Reihenfolge interessiert sind, invariant gegenüber einfacher Translation und Skalierung sein sollte, der in der metrischen MDS verwendete Stress jedoch empfindlich auf Skalierung reagiert. Um dies zu beheben, gibt nicht-metrische MDS normalisierten Stress zurück, auch bekannt als Stress-1, definiert als

\[\sqrt{\frac{\sum_{i < j} (\hat{d}_{ij} - d_{ij}(Z))^2}{\sum_{i < j} d_{ij}(Z)^2}}.\]

Normalisierter Stress-1 wird zurückgegeben, wenn normalized_stress=True ist.

Klassische MDS, auch bekannt als Principal Coordinates Analysis (PCoA) oder Torgerson’s Scaling, wird in der separaten Klasse ClassicalMDS implementiert. Klassische MDS ersetzt die Stress-Verlustfunktion durch eine andere Verlustfunktion namens Strain, die eine exakte Lösung in Form einer Eigenwertzerlegung hat. Wenn die Dissimilaritätsmatrix aus den paarweisen euklidischen Abständen zwischen einigen Vektoren besteht, dann ist klassische MDS äquivalent zu PCA, angewendet auf diese Menge von Vektoren.

Formal ist die Verlustfunktion der klassischen MDS (Strain) gegeben durch

\[\frac{\|B - ZZ^T\|_F}{\|B\|_F} =\sqrt{\frac{\sum_{i,j} (b_{ij} - z_i^\top z_j)^2}{\sum_{i,j} b_{ij}^2}},\]

wobei \(Z\) die \(n \times d\)-Einbettungsmatrix ist, deren Zeilen \(z_i^T\) sind, \(\|\cdot\|_F\) die Frobenius-Norm bezeichnet und \(B\) die Gram-Matrix mit Elementen \(b_{ij}\) ist, gegeben durch \(B = -\frac{1}{2}C\Delta C\). Hier ist \(C\Delta C\) die doppelt zentrierte Matrix der quadrierten Dissimiliaritäten, wobei \(\Delta\) die Matrix der quadrierten Eingabe-Dissimiliaritäten \(\delta^2_{ij}\) und \(C=I-J/n\) die Zentrierungsmatrix ist (Einheitsmatrix minus einer Matrix aus Einsen geteilt durch \(n\)). Dies kann exakt mithilfe der Eigenwertzerlegung von \(B\) minimiert werden.

Referenzen

• „More on Multidimensional Scaling and Unfolding in R: smacof Version 2“ Mair P, Groenen P., de Leeuw J. Journal of Statistical Software (2022)

• „Modern Multidimensional Scaling - Theory and Applications“ Borg, I.; Groenen P. Springer Series in Statistics (1997)

• „Nonmetric multidimensional scaling: a numerical method“ Kruskal, J. Psychometrika, 29 (1964)

• „Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis“ Kruskal, J. Psychometrika, 29, (1964)

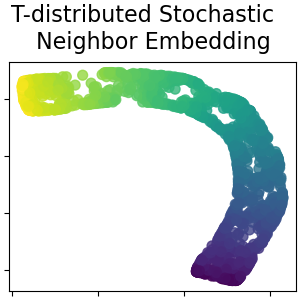
2.2.9. t-verteilte stochastische Nachbar-Einbettung (t-SNE)

t-SNE (TSNE) wandelt Affinitäten von Datenpunkten in Wahrscheinlichkeiten um. Die Affinitäten im Originalraum werden durch Gaußsche gemeinsame Wahrscheinlichkeiten repräsentiert und die Affinitäten im eingebetteten Raum durch Student-t-Verteilungen. Dies ermöglicht es t-SNE, besonders empfindlich für lokale Struktur zu sein und hat einige andere Vorteile gegenüber bestehenden Techniken

• Offenlegung der Struktur auf vielen Skalen auf einer einzigen Karte

• Offenlegung von Daten, die in mehreren unterschiedlichen Mannigfaltigkeiten oder Clustern liegen

• Reduzierung der Tendenz, Punkte in der Mitte zu gruppieren

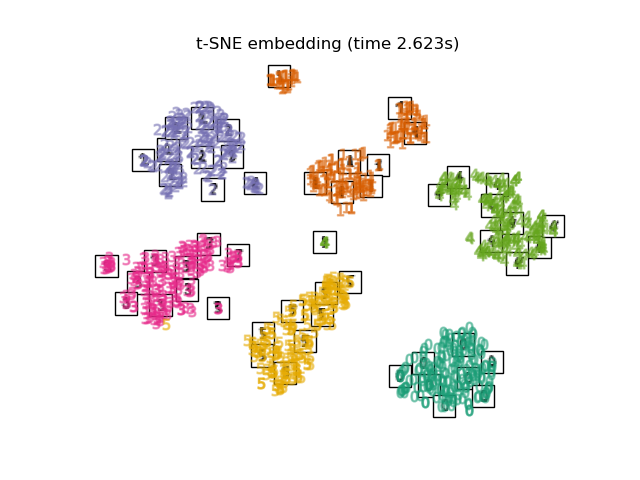
Während Isomap, LLE und Varianten am besten geeignet sind, um eine einzelne kontinuierliche niederdimensionale Mannigfaltigkeit zu entfalten, konzentriert sich t-SNE auf die lokale Struktur der Daten und neigt dazu, gruppierte lokale Stichprobengruppen zu extrahieren, wie im S-Kurven-Beispiel hervorgehoben. Diese Fähigkeit, Stichproben basierend auf der lokalen Struktur zu gruppieren, kann vorteilhaft sein, um einen Datensatz visuell zu entwirren, der mehrere Mannigfaltigkeiten gleichzeitig umfasst, wie dies beim Zifferndatensatz der Fall ist.

Die Kullback-Leibler (KL)-Divergenz der gemeinsamen Wahrscheinlichkeiten im ursprünglichen Raum und im eingebetteten Raum wird durch Gradientenabstieg minimiert. Beachten Sie, dass die KL-Divergenz nicht konvex ist, d. h. mehrere Neustarts mit unterschiedlichen Initialisierungen führen zu lokalen Minima der KL-Divergenz. Daher ist es manchmal nützlich, verschiedene Seeds auszuprobieren und die Einbettung mit der niedrigsten KL-Divergenz auszuwählen.

Die Nachteile der Verwendung von t-SNE sind ungefähr

• t-SNE ist rechenintensiv und kann Stunden für Datensätze mit Millionen von Stichproben dauern, während PCA in Sekunden oder Minuten abgeschlossen ist.

• Die Barnes-Hut-t-SNE-Methode ist auf zweioder dreidimensionale Einbettungen beschränkt.

• Der Algorithmus ist stochastisch, und mehrere Neustarts mit verschiedenen Seeds können zu unterschiedlichen Einbettungen führen. Es ist jedoch durchaus legitim, die Einbettung mit dem geringsten Fehler auszuwählen.

• Die globale Struktur wird nicht explizit erhalten. Dieses Problem wird gemildert, indem Punkte mit PCA initialisiert werden (mit init='pca').

Optimieren von t-SNE

Der Hauptzweck von t-SNE ist die Visualisierung hochdimensionaler Daten. Daher funktioniert es am besten, wenn die Daten in zwei oder drei Dimensionen eingebettet werden.

Die Optimierung der KL-Divergenz kann manchmal etwas knifflig sein. Es gibt fünf Parameter, die die Optimierung von t-SNE und damit möglicherweise die Qualität der resultierenden Einbettung steuern

• Perplexität

• Faktor der frühen Überbetonung

• Lernrate

• maximale Anzahl von Iterationen

• Winkel (nicht in der exakten Methode verwendet)

Die Perplexität ist definiert als \(k=2^{(S)}\), wobei \(S\) die Shannon-Entropie der bedingten Wahrscheinlichkeitsverteilung ist. Die Perplexität eines \(k\)-seitigen Würfels ist \(k\), so dass \(k\) effektiv die Anzahl der nächsten Nachbarn ist, die t-SNE bei der Erzeugung der bedingten Wahrscheinlichkeiten berücksichtigt. Größere Perplexitäten führen zu mehr nächsten Nachbarn und sind weniger empfindlich gegenüber kleinen Strukturen. Umgekehrt berücksichtigt eine geringere Perplexität eine geringere Anzahl von Nachbarn und ignoriert daher mehr globale Informationen zugunsten der lokalen Nachbarschaft. Wenn die Datensatzgrößen größer werden, werden mehr Punkte benötigt, um eine angemessene Stichprobe der lokalen Nachbarschaft zu erhalten, und daher können größere Perplexitäten erforderlich sein. Ebenso erfordern verrauschtere Datensätze größere Perplexitätswerte, um genügend lokale Nachbarn einzuschließen, um über das Hintergrundrauschen hinaus zu sehen.

Die maximale Anzahl von Iterationen ist normalerweise hoch genug und muss nicht angepasst werden. Die Optimierung besteht aus zwei Phasen: der Phase der frühen Überbetonung und der endgültigen Optimierung. Während der frühen Überbetonung werden die gemeinsamen Wahrscheinlichkeiten im ursprünglichen Raum künstlich erhöht, indem sie mit einem gegebenen Faktor multipliziert werden. Größere Faktoren führen zu größeren Abständen zwischen natürlichen Clustern in den Daten. Wenn der Faktor zu hoch ist, könnte die KL-Divergenz in dieser Phase zunehmen. Normalerweise muss sie nicht abgestimmt werden. Ein kritischer Parameter ist die Lernrate. Wenn sie zu niedrig ist, gerät der Gradientenabstieg in einem schlechten lokalen Minimum stecken. Wenn sie zu hoch ist, steigt die KL-Divergenz während der Optimierung. Eine in Belkina et al. (2019) vorgeschlagene Heuristik ist, die Lernrate auf die Stichprobengröße geteilt durch den Faktor der frühen Überbetonung einzustellen. Wir implementieren diese Heuristik als Argument learning_rate='auto'. Weitere Tipps finden Sie in Laurens van der Maatens FAQ (siehe Referenzen). Der letzte Parameter, Winkel, ist ein Kompromiss zwischen Leistung und Genauigkeit. Größere Winkel bedeuten, dass wir größere Regionen durch einen einzelnen Punkt annähern können, was zu besserer Geschwindigkeit, aber weniger genauen Ergebnissen führt.

„How to Use t-SNE Effectively“ bietet eine gute Diskussion über die Auswirkungen der verschiedenen Parameter sowie interaktive Diagramme zur Erkundung der Auswirkungen verschiedener Parameter.

Barnes-Hut t-SNE

Das hier implementierte Barnes-Hut t-SNE ist in der Regel viel langsamer als andere Mannigfaltigkeitslernalgorithmen. Die Optimierung ist ziemlich schwierig und die Berechnung des Gradienten ist \(O[d N log(N)]\), wobei \(d\) die Anzahl der Ausgabedimensionen und \(N\) die Anzahl der Stichproben ist. Die Barnes-Hut-Methode verbessert die exakte Methode, bei der die Komplexität von t-SNE \(O[d N^2]\) beträgt, weist jedoch mehrere andere bemerkenswerte Unterschiede auf.

• Die Barnes-Hut-Implementierung funktioniert nur, wenn die Ziel-Dimensionalität 3 oder weniger beträgt. Der 2D-Fall ist typisch für den Aufbau von Visualisierungen.

• Barnes-Hut funktioniert nur mit dichten Eingabedaten. Dichte Datenmatrizen können nur mit der exakten Methode eingebettet werden oder können durch eine dichte niedrigrangige Projektion approximiert werden, z. B. mit PCA

• Barnes-Hut ist eine Annäherung an die exakte Methode. Die Annäherung wird mit dem Winkelparameter parametrisiert, daher wird der Winkelparameter bei der Methode="exact" nicht verwendet.

• Barnes-Hut ist signifikant besser skalierbar. Barnes-Hut kann verwendet werden, um Hunderttausende von Datenpunkten einzubetten, während die exakte Methode Tausende von Stichproben handhaben kann, bevor sie rechentechnisch untragbar wird.

Für Visualisierungszwecke (was der Haupteinsatzfall von t-SNE ist) wird die Verwendung der Barnes-Hut-Methode dringend empfohlen. Die exakte t-SNE-Methode ist nützlich, um die theoretischen Eigenschaften der Einbettung möglicherweise in höherdimensionalen Räumen zu überprüfen, ist jedoch aufgrund rechnerischer Einschränkungen auf kleine Datensätze beschränkt.

Beachten Sie auch, dass die Ziffernetiketten grob mit der von t-SNE gefundenen natürlichen Gruppierung übereinstimmen, während die lineare 2D-Projektion des PCA-Modells eine Darstellung ergibt, bei der sich die Etikettenbereiche weitgehend überlappen. Dies ist ein starker Hinweis darauf, dass diese Daten gut durch nichtlineare Methoden getrennt werden können, die sich auf die lokale Struktur konzentrieren (z. B. ein SVM mit einem Gaußschen RBF-Kernel). Das Versagen, gut getrennte, homogen etikettierte Gruppen mit t-SNE in 2D zu visualisieren, impliziert jedoch nicht notwendigerweise, dass die Daten nicht korrekt von einem überwachten Modell klassifiziert werden können. Es könnte der Fall sein, dass 2 Dimensionen nicht hoch genug sind, um die interne Struktur der Daten genau darzustellen.

Referenzen

• „Visualizing High-Dimensional Data Using t-SNE“ van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)

• „t-Distributed Stochastic Neighbor Embedding“ van der Maaten, L.J.P.

• „Accelerating t-SNE using Tree-Based Algorithms“ van der Maaten, L.J.P.; Journal of Machine Learning Research 15(Okt):3221-3245, 2014.

• „Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets“ Belkina, A.C., Ciccolella, C.O., Anno, R., Halpert, R., Spidlen, J., Snyder-Cappione, J.E., Nature Communications 10, 5415 (2019).

2.2.10. Tipps zur praktischen Anwendung

• Stellen Sie sicher, dass für alle Merkmale die gleiche Skala verwendet wird. Da Mannigfaltigkeitslernmethoden auf einer Nächste-Nachbarn-Suche basieren, kann der Algorithmus andernfalls schlecht funktionieren. Siehe StandardScaler für praktische Möglichkeiten zur Skalierung heterogener Daten.

• Der von jeder Routine berechnete Rekonstruktionsfehler kann zur Auswahl der optimalen Ausgabedimension verwendet werden. Für eine \(d\)-dimensionale Mannigfaltigkeit, die in einen \(D\)-dimensionalen Parameterraum eingebettet ist, wird der Rekonstruktionsfehler mit zunehmender Anzahl von n_components abnehmen, bis n_components == d.

• Beachten Sie, dass verrauschte Daten die Mannigfaltigkeit "kurzschließen" können und im Wesentlichen als Brücke zwischen Teilen der Mannigfaltigkeit dienen, die sonst gut getrennt wären. Mannigfaltigkeitslernen auf verrauschten und/oder unvollständigen Daten ist ein aktives Forschungsgebiet.

• Bestimmte Eingabekonfigurationen können zu singulären Gewichtsmatrizen führen, z. B. wenn mehr als zwei Punkte im Datensatz identisch sind oder wenn die Daten in disjunkte Gruppen aufgeteilt sind. In diesem Fall kann solver='arpack' den Nullraum nicht finden. Die einfachste Lösung hierfür ist die Verwendung von solver='dense', das auf einer singulären Matrix funktioniert, aber je nach Anzahl der Eingabepunkte sehr langsam sein kann. Alternativ kann man versuchen, die Ursache der Singularität zu ermitteln: Wenn sie auf disjunkte Mengen zurückzuführen ist, kann eine Erhöhung von n_neighbors helfen. Wenn sie auf identische Punkte im Datensatz zurückzuführen ist, kann das Entfernen dieser Punkte helfen.

Siehe auch

Totally Random Trees Embedding kann auch nützlich sein, um nichtlineare Darstellungen des Merkmalsraums abzuleiten, führt aber keine Dimensionsreduktion durch.