Multi-dimensional Scaling

Eine Veranschaulichung von metrischem und nicht-metrischem MDS anhand von generierten verrauschten Daten.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Dataset-Vorbereitung

Wir beginnen damit, 20 Punkte gleichmäßig in einem 2D-Raum zu generieren.

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.collections import LineCollection

from sklearn import manifold
from sklearn.decomposition import PCA
from sklearn.metrics import euclidean_distances

# Generate the data
EPSILON = np.finfo(np.float32).eps
n_samples = 20
rng = np.random.RandomState(seed=3)
X_true = rng.randint(0, 20, 2 * n_samples).astype(float)
X_true = X_true.reshape((n_samples, 2))

# Center the data
X_true -= X_true.mean()

Nun berechnen wir die paarweisen Abstände zwischen allen Punkten und fügen der Distanzmatrix eine geringe Menge Rauschen hinzu. Wir stellen sicher, dass die verrauschte Distanzmatrix symmetrisch bleibt.

# Compute pairwise Euclidean distances
distances = euclidean_distances(X_true)

# Add noise to the distances
noise = rng.rand(n_samples, n_samples)
noise = noise + noise.T
np.fill_diagonal(noise, 0)
distances += noise

Hier berechnen wir metrisches, nicht-metrisches und klassisches MDS der verrauschten Distanzmatrix.

mds = manifold.MDS(
    n_components=2,
    max_iter=3000,
    eps=1e-9,
    n_init=1,
    random_state=42,
    metric="precomputed",
    n_jobs=1,
    init="classical_mds",
)
X_mds = mds.fit(distances).embedding_

nmds = manifold.MDS(
    n_components=2,
    metric_mds=False,
    max_iter=3000,
    eps=1e-12,
    metric="precomputed",
    random_state=42,
    n_jobs=1,
    n_init=1,
    init="classical_mds",
)
X_nmds = nmds.fit_transform(distances)

cmds = manifold.ClassicalMDS(
    n_components=2,
    metric="precomputed",
)
X_cmds = cmds.fit_transform(distances)

Neuskalierung der nicht-metrischen MDS-Lösung, um die Streuung der ursprünglichen Daten anzupassen.

X_nmds *= np.sqrt((X_true**2).sum()) / np.sqrt((X_nmds**2).sum())

Um die visuellen Vergleiche zu erleichtern, drehen wir die ursprünglichen Daten und alle MDS-Lösungen auf ihre PCA-Achsen. Und spiegeln bei Bedarf horizontale und vertikale MDS-Achsen, um die Ausrichtung der ursprünglichen Daten anzupassen.

# Rotate the data (CMDS does not need to be rotated, it is inherently PCA-aligned)
pca = PCA(n_components=2)
X_true = pca.fit_transform(X_true)
X_mds = pca.fit_transform(X_mds)
X_nmds = pca.fit_transform(X_nmds)

# Align the sign of PCs
for i in [0, 1]:
    if np.corrcoef(X_mds[:, i], X_true[:, i])[0, 1] < 0:
        X_mds[:, i] *= -1
    if np.corrcoef(X_nmds[:, i], X_true[:, i])[0, 1] < 0:
        X_nmds[:, i] *= -1
    if np.corrcoef(X_cmds[:, i], X_true[:, i])[0, 1] < 0:
        X_cmds[:, i] *= -1

Schließlich plotten wir die ursprünglichen Daten und alle MDS-Rekonstruktionen.

fig = plt.figure(1)
ax = plt.axes([0.0, 0.0, 1.0, 1.0])

s = 100
plt.scatter(X_true[:, 0], X_true[:, 1], color="navy", s=s, lw=0, label="True Position")
plt.scatter(X_mds[:, 0], X_mds[:, 1], color="turquoise", s=s, lw=0, label="MDS")
plt.scatter(
    X_nmds[:, 0], X_nmds[:, 1], color="darkorange", s=s, lw=0, label="Non-metric MDS"
)
plt.scatter(
    X_cmds[:, 0], X_cmds[:, 1], color="lightcoral", s=s, lw=0, label="Classical MDS"
)
plt.legend(scatterpoints=1, loc="best", shadow=False)

# Plot the edges
start_idx, end_idx = X_mds.nonzero()
# a sequence of (*line0*, *line1*, *line2*), where::
#            linen = (x0, y0), (x1, y1), ... (xm, ym)
segments = [
    [X_true[i, :], X_true[j, :]] for i in range(len(X_true)) for j in range(len(X_true))
]
edges = distances.max() / (distances + EPSILON) * 100
np.fill_diagonal(edges, 0)
edges = np.abs(edges)
lc = LineCollection(
    segments, zorder=0, cmap=plt.cm.Blues, norm=plt.Normalize(0, edges.max())
)
lc.set_array(edges.flatten())
lc.set_linewidths(np.full(len(segments), 0.5))
ax.add_collection(lc)

plt.show()

Verwandte Beispiele

Vergleich von Manifold Learning Methoden

Vergleich von Manifold Learning Methoden

Manifold Learning Methoden auf einer abgetrennten Sphäre

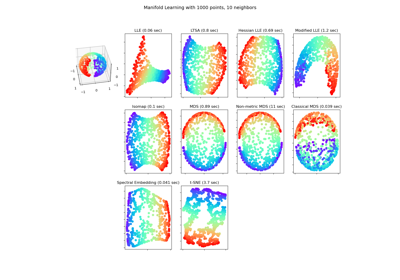
Manifold Learning Methoden auf einer abgetrennten Sphäre

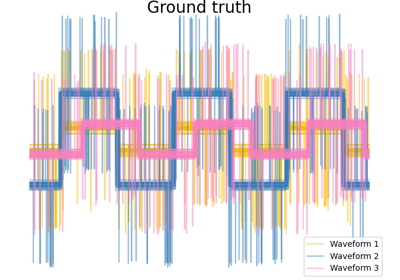
Agglomeratives Clustering mit verschiedenen Metriken

Agglomeratives Clustering mit verschiedenen Metriken

Die Johnson-Lindenstrauss-Schranke für Einbettung mit zufälligen Projektionen

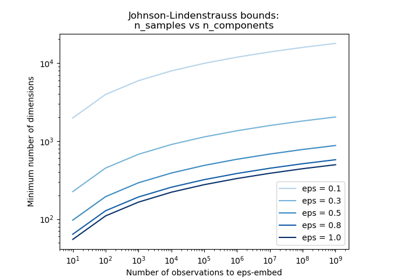
Die Johnson-Lindenstrauss-Schranke für Einbettung mit zufälligen Projektionen