Verwendung von KBinsDiscretizer zur Diskretisierung kontinuierlicher Merkmale

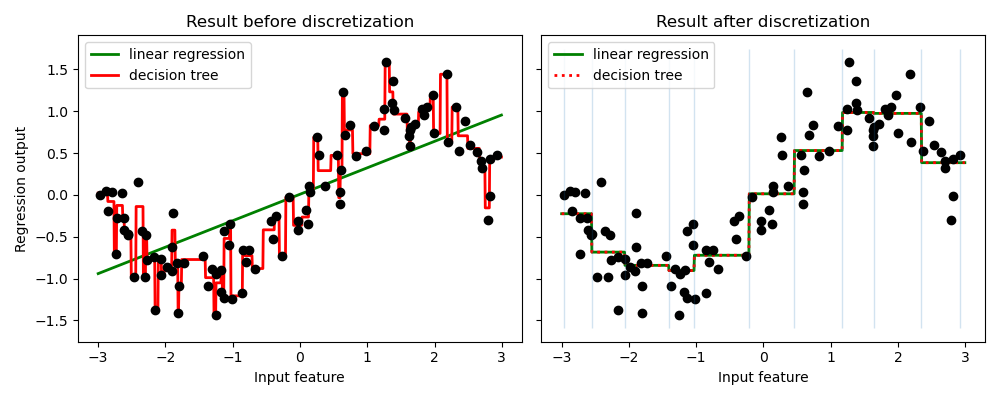
Das Beispiel vergleicht die Vorhersageergebnisse der linearen Regression (lineares Modell) und des Entscheidungsbaums (baumartiges Modell) mit und ohne Diskretisierung von reellwertigen Merkmalen.

Wie im Ergebnis vor der Diskretisierung gezeigt, ist das lineare Modell schnell zu erstellen und relativ einfach zu interpretieren, kann aber nur lineare Beziehungen modellieren, während der Entscheidungsbaum ein viel komplexeres Modell der Daten erstellen kann. Eine Möglichkeit, ein lineares Modell bei kontinuierlichen Daten leistungsfähiger zu machen, ist die Verwendung von Diskretisierung (auch als Binning bekannt). Im Beispiel diskretisieren wir das Merkmal und führen eine One-Hot-Kodierung der transformierten Daten durch. Beachten Sie, dass bei nicht ausreichend breiten Bins ein erheblich erhöhtes Risiko des Overfittings besteht, daher sollten die Parameter des Diskretisierers normalerweise unter Kreuzvalidierung abgestimmt werden.

Nach der Diskretisierung machen lineare Regression und Entscheidungsbaum exakt dieselbe Vorhersage. Da die Merkmale innerhalb jedes Bins konstant sind, muss jedes Modell denselben Wert für alle Punkte innerhalb eines Bins vorhersagen. Verglichen mit dem Ergebnis vor der Diskretisierung wird das lineare Modell viel flexibler, während der Entscheidungsbaum viel weniger flexibel wird. Beachten Sie, dass das Binning von Merkmalen für baumartige Modelle im Allgemeinen keinen vorteilhaften Effekt hat, da diese Modelle lernen können, die Daten überall aufzuteilen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

# construct the dataset
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)

# transform the dataset with KBinsDiscretizer
enc = KBinsDiscretizer(
    n_bins=10, encode="onehot", quantile_method="averaged_inverted_cdf"
)
X_binned = enc.fit_transform(X)

# predict with original dataset
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="green", label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="red", label="decision tree")
ax1.plot(X[:, 0], y, "o", c="k")
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

# predict with transformed dataset
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="green",
    linestyle="-",
    label="linear regression",
)
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="red",
    linestyle=":",
    label="decision tree",
)
ax2.plot(X[:, 0], y, "o", c="k")
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=0.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")

plt.tight_layout()
plt.show()

Verwandte Beispiele

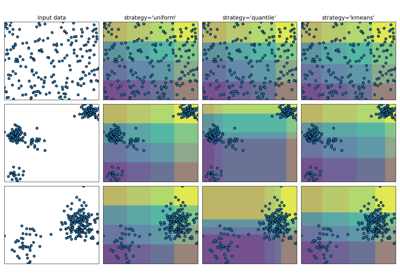
Demonstration der verschiedenen Strategien von KBinsDiscretizer

Demonstration der verschiedenen Strategien von KBinsDiscretizer

Kurvenanpassung mit Bayes'scher Ridge-Regression

Kurvenanpassung mit Bayes'scher Ridge-Regression

Gradient Boosting Regression

Gradient Boosting Regression

Entscheidungsbaum-Regression

Entscheidungsbaum-Regression