Illustration der Nachbarschaftskomponentenanalyse

Dieses Beispiel illustriert eine erlernte Distanzmetrik, die die Klassifizierungsgenauigkeit der nächsten Nachbarn maximiert. Es bietet eine visuelle Darstellung dieser Metrik im Vergleich zum ursprünglichen Punktraum. Weitere Informationen finden Sie im Benutzerhandbuch.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from scipy.special import logsumexp

from sklearn.datasets import make_classification
from sklearn.neighbors import NeighborhoodComponentsAnalysis

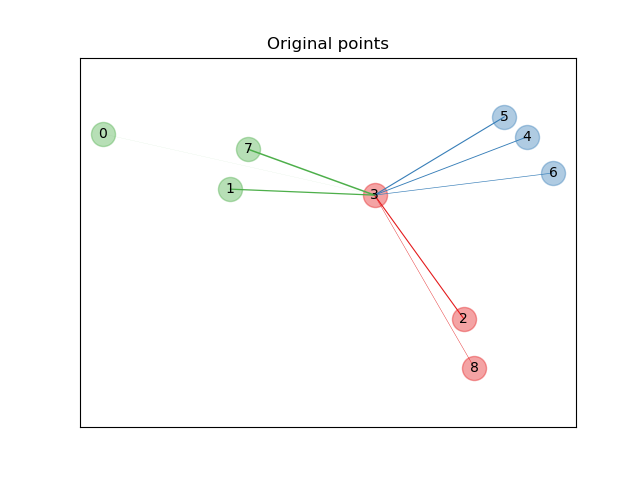
Ursprüngliche Punkte

Zuerst erstellen wir einen Datensatz mit 9 Stichproben aus 3 Klassen und plotten die Punkte im ursprünglichen Raum. Für dieses Beispiel konzentrieren wir uns auf die Klassifizierung des Punktes Nr. 3. Die Dicke einer Verbindung zwischen Punkt Nr. 3 und einem anderen Punkt ist proportional zu ihrer Distanz.

X, y = make_classification(
    n_samples=9,
    n_features=2,
    n_informative=2,
    n_redundant=0,
    n_classes=3,
    n_clusters_per_class=1,
    class_sep=1.0,
    random_state=0,
)

plt.figure(1)
ax = plt.gca()
for i in range(X.shape[0]):
    ax.text(X[i, 0], X[i, 1], str(i), va="center", ha="center")
    ax.scatter(X[i, 0], X[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)

ax.set_title("Original points")
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
ax.axis("equal")  # so that boundaries are displayed correctly as circles


def link_thickness_i(X, i):
    diff_embedded = X[i] - X
    dist_embedded = np.einsum("ij,ij->i", diff_embedded, diff_embedded)
    dist_embedded[i] = np.inf

    # compute exponentiated distances (use the log-sum-exp trick to
    # avoid numerical instabilities
    exp_dist_embedded = np.exp(-dist_embedded - logsumexp(-dist_embedded))
    return exp_dist_embedded


def relate_point(X, i, ax):
    pt_i = X[i]
    for j, pt_j in enumerate(X):
        thickness = link_thickness_i(X, i)
        if i != j:
            line = ([pt_i[0], pt_j[0]], [pt_i[1], pt_j[1]])
            ax.plot(*line, c=cm.Set1(y[j]), linewidth=5 * thickness[j])


i = 3
relate_point(X, i, ax)
plt.show()

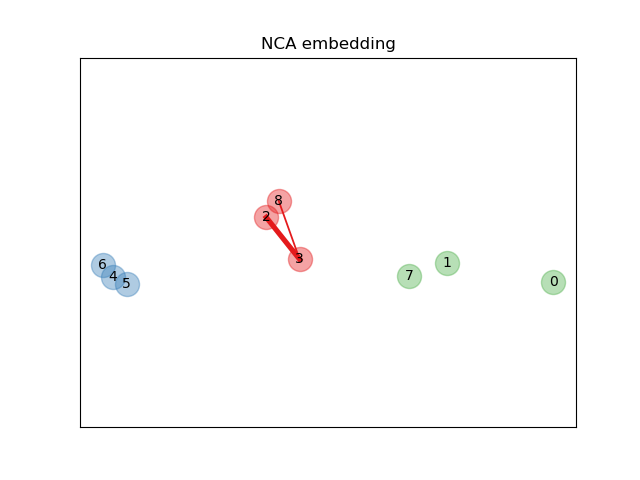
Erlernen einer Einbettung

Wir verwenden NeighborhoodComponentsAnalysis, um eine Einbettung zu erlernen und die Punkte nach der Transformation zu plotten. Dann nehmen wir die Einbettung und finden die nächsten Nachbarn.

nca = NeighborhoodComponentsAnalysis(max_iter=30, random_state=0)
nca = nca.fit(X, y)

plt.figure(2)
ax2 = plt.gca()
X_embedded = nca.transform(X)
relate_point(X_embedded, i, ax2)

for i in range(len(X)):
    ax2.text(X_embedded[i, 0], X_embedded[i, 1], str(i), va="center", ha="center")
    ax2.scatter(X_embedded[i, 0], X_embedded[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)

ax2.set_title("NCA embedding")
ax2.axes.get_xaxis().set_visible(False)
ax2.axes.get_yaxis().set_visible(False)
ax2.axis("equal")
plt.show()

Verwandte Beispiele

Vergleich von Nächsten Nachbarn mit und ohne Neighborhood Components Analysis

Vergleich von Nächsten Nachbarn mit und ohne Neighborhood Components Analysis

Dimensionsreduktion mit Neighborhood Components Analysis

Dimensionsreduktion mit Neighborhood Components Analysis

Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

Mannigfaltigkeitslernen auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap...

Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch

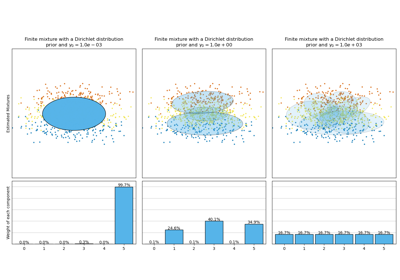
Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch