1.6. Nächste Nachbarn

sklearn.neighbors bietet Funktionalität für unüberwachte und überwachte Methoden, die auf Nachbarn basieren. Unüberwachte Nachbarschafts-Methoden sind die Grundlage vieler anderer Lernmethoden, insbesondere Manifold Learning und Spektrale Clusterbildung. Überwachtes Nachbarschafts-Lernen gibt es in zwei Varianten: Klassifikation für Daten mit diskreten Labels und Regression für Daten mit kontinuierlichen Labels.

Das Prinzip hinter Nachbarschafts-Methoden besteht darin, eine vordefinierte Anzahl von Trainingsbeispielen zu finden, die dem neuen Punkt am nächsten sind, und das Label aus diesen vorherzusagen. Die Anzahl der Beispiele kann eine benutzerdefinierte Konstante (k-Nächste-Nachbar-Lernen) sein oder basierend auf der lokalen Dichte der Punkte variieren (radiusbasierte Nachbarschafts-Lernen). Die Distanz kann im Allgemeinen jede metrische Messung sein: Die Standard-Euklidische Distanz ist die gebräuchlichste Wahl. Nachbarschafts-basierte Methoden werden als nicht-generalisierende Machine-Learning-Methoden bezeichnet, da sie einfach alle ihre Trainingsdaten „erinnern“ (möglicherweise in eine schnelle Indexierungsstruktur wie einen Ball Tree oder KD Tree umgewandelt).

Trotz seiner Einfachheit war die Methode der nächsten Nachbarn bei einer großen Anzahl von Klassifikations- und Regressionsproblemen erfolgreich, einschließlich handgeschriebener Ziffern und Szenen von Satellitenbildern. Als nicht-parametrische Methode ist sie oft erfolgreich in Klassifikationssituationen, in denen die Entscheidungsgrenze sehr unregelmäßig ist.

Die Klassen in sklearn.neighbors können sowohl NumPy-Arrays als auch scipy.sparse Matrizen als Eingabe verarbeiten. Für dichte Matrizen wird eine große Anzahl möglicher Distanzmetriken unterstützt. Für sparse Matrizen werden beliebige Minkowski-Metriken für Suchen unterstützt.

Es gibt viele Lernroutinen, die auf der Kernfunktionalität von Nächsten Nachbarn basieren. Ein Beispiel ist die Kernel-Dichteschätzung, die im Abschnitt zur Dichteschätzung diskutiert wird.

1.6.1. Unüberwachte Nächste Nachbarn

NearestNeighbors implementiert unüberwachtes Nachbarschafts-Lernen. Es fungiert als einheitliche Schnittstelle zu drei verschiedenen Algorithmen für die Suche nach nächsten Nachbarn: BallTree, KDTree und ein Brute-Force-Algorithmus, der auf Routinen in sklearn.metrics.pairwise basiert. Die Wahl des Nachbarschaftssuchalgorithmus wird über das Schlüsselwort 'algorithm' gesteuert, das einer der folgenden Werte sein muss: ['auto', 'ball_tree', 'kd_tree', 'brute']. Wenn der Standardwert 'auto' übergeben wird, versucht der Algorithmus, den besten Ansatz anhand der Trainingsdaten zu ermitteln. Eine Diskussion der Stärken und Schwächen jeder Option finden Sie unter Nächste-Nachbarn-Algorithmen.

Warnung

Bezüglich der Algorithmen für nächste Nachbarn gilt: Wenn zwei Nachbarn \(k+1\) und \(k\) identische Distanzen, aber unterschiedliche Labels haben, hängt das Ergebnis von der Reihenfolge der Trainingsdaten ab.

1.6.1.1. Finden der nächsten Nachbarn

Für die einfache Aufgabe, die nächsten Nachbarn zwischen zwei Datensätzen zu finden, können die unüberwachten Algorithmen innerhalb von sklearn.neighbors verwendet werden.

>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)
>>> distances
array([[0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356],
       [0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356]])

Da der Abfragesatz mit dem Trainingssatz übereinstimmt, ist der nächste Nachbar jedes Punktes der Punkt selbst mit einer Distanz von Null.

Es ist auch möglich, effizient einen dünnbesetzten Graphen zu erstellen, der die Verbindungen zwischen benachbarten Punkten zeigt.

>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 1., 1., 0., 0., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 0., 1., 1.]])

Der Datensatz ist so strukturiert, dass Punkte, die in der Indexreihenfolge nahe beieinander liegen, im Parameterraum ebenfalls nahe beieinander liegen, was zu einer annähernd blockdiagonalen Matrix von K-nächsten Nachbarn führt. Ein solcher dünnbesetzter Graph ist in einer Vielzahl von Umgebungen nützlich, die räumliche Beziehungen zwischen Punkten für unüberwachtes Lernen nutzen: insbesondere siehe Isomap, LocallyLinearEmbedding und SpectralClustering.

1.6.1.2. KDTree und BallTree Klassen

Alternativ kann man direkt die Klassen KDTree oder BallTree verwenden, um nächste Nachbarn zu finden. Dies ist die Funktionalität, die von der oben verwendeten Klasse NearestNeighbors umschlossen wird. Die Ball Tree und KD Tree haben die gleiche Schnittstelle; wir zeigen hier ein Beispiel für die Verwendung des KD Tree.

>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)

Beziehen Sie sich auf die Dokumentation der Klassen KDTree und BallTree für weitere Informationen über die Optionen, die für die Suche nach nächsten Nachbarn verfügbar sind, einschließlich der Spezifikation von Abfragestrategien, Distanzmetriken usw. Eine Liste gültiger Metriken erhalten Sie über KDTree.valid_metrics und BallTree.valid_metrics.

>>> from sklearn.neighbors import KDTree, BallTree
>>> KDTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity']
>>> BallTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity', 'seuclidean', 'mahalanobis', 'hamming', 'canberra', 'braycurtis', 'jaccard', 'dice', 'rogerstanimoto', 'russellrao', 'sokalmichener', 'sokalsneath', 'haversine', 'pyfunc']

1.6.2. Klassifikation mit nächsten Nachbarn

Nachbarschafts-basierte Klassifikation ist eine Art von Instanz-basiertem Lernen oder nicht-generalisierendem Lernen: Sie versucht nicht, ein allgemeines internes Modell zu konstruieren, sondern speichert einfach Instanzen der Trainingsdaten. Die Klassifikation wird aus einer einfachen Mehrheitswahl der nächsten Nachbarn jedes Punktes berechnet: Ein Abfragepunkt wird der Datenklasse zugeordnet, die die meisten Repräsentanten innerhalb der nächsten Nachbarn des Punktes hat.

scikit-learn implementiert zwei verschiedene Klassifikatoren für nächste Nachbarn: KNeighborsClassifier implementiert das Lernen basierend auf den \(k\) nächsten Nachbarn jedes Abfragepunktes, wobei \(k\) ein vom Benutzer angegebener ganzzahliger Wert ist. RadiusNeighborsClassifier implementiert das Lernen basierend auf der Anzahl der Nachbarn innerhalb eines festen Radius \(r\) jedes Trainingspunktes, wobei \(r\) ein vom Benutzer angegebener Fließkommawert ist.

Die \(k\)-Nächste-Nachbarn-Klassifikation in KNeighborsClassifier ist die am häufigsten verwendete Technik. Die optimale Wahl des Wertes \(k\) ist stark datenabhängig: Im Allgemeinen unterdrückt ein größeres \(k\) die Effekte von Rauschen, macht aber die Klassifikationsgrenzen weniger deutlich.

In Fällen, in denen die Daten nicht gleichmäßig gesampelt sind, kann die radiusbasierte Nachbarschaftsklassifikation in RadiusNeighborsClassifier eine bessere Wahl sein. Der Benutzer gibt einen festen Radius \(r\) an, so dass Punkte in spärlicheren Nachbarschaften weniger nächste Nachbarn für die Klassifikation verwenden. In hochdimensionalen Parameterbereichen wird diese Methode aufgrund des sogenannten „Fluchs der Dimensionalität“ weniger effektiv.

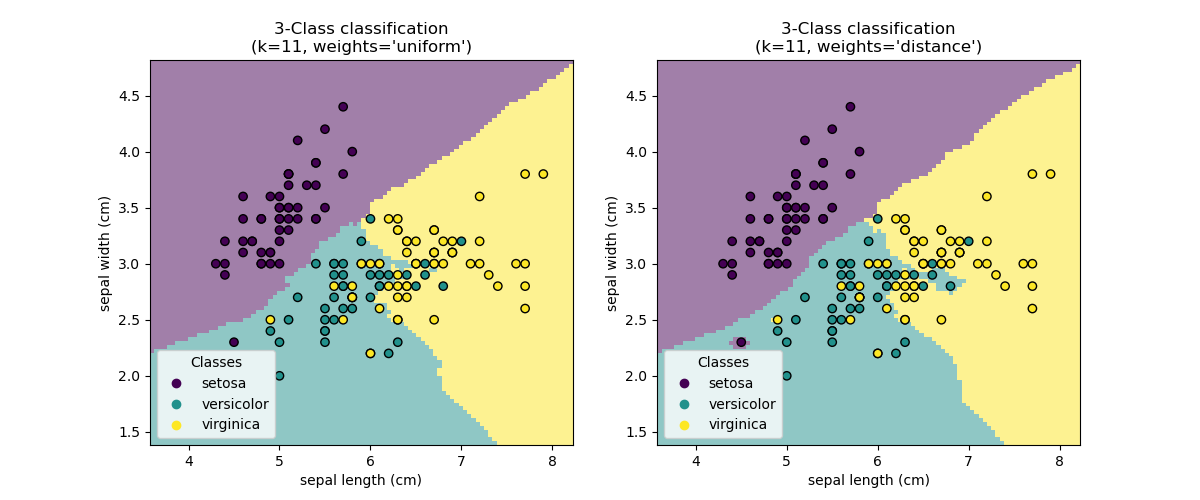
Die grundlegende Nächste-Nachbarn-Klassifikation verwendet gleichmäßige Gewichte: Das heißt, der Wert, der einem Abfragepunkt zugewiesen wird, wird aus einer einfachen Mehrheitswahl der nächsten Nachbarn berechnet. Unter bestimmten Umständen ist es besser, die Nachbarn zu gewichten, so dass nähere Nachbarn stärker zum Fit beitragen. Dies kann durch das Schlüsselwort weights erreicht werden. Der Standardwert weights = 'uniform' weist jedem Nachbarn einheitliche Gewichte zu. weights = 'distance' weist Gewichte zu, die proportional zum Kehrwert der Distanz vom Abfragepunkt sind. Alternativ kann eine benutzerdefinierte Funktion der Distanz bereitgestellt werden, die zur Berechnung der Gewichte verwendet wird.

Beispiele

• Klassifikation mit Nächsten Nachbarn: ein Beispiel für Klassifikation unter Verwendung von Nächsten Nachbarn.

1.6.3. Regression mit nächsten Nachbarn

Nachbarschafts-basierte Regression kann in Fällen verwendet werden, in denen die Daten-Labels kontinuierliche statt diskrete Variablen sind. Das Label, das einem Abfragepunkt zugewiesen wird, wird basierend auf dem Mittelwert der Labels seiner nächsten Nachbarn berechnet.

scikit-learn implementiert zwei verschiedene Nachbarschafts-Regressoren: KNeighborsRegressor implementiert das Lernen basierend auf den \(k\) nächsten Nachbarn jedes Abfragepunktes, wobei \(k\) ein vom Benutzer angegebener ganzzahliger Wert ist. RadiusNeighborsRegressor implementiert das Lernen basierend auf den Nachbarn innerhalb eines festen Radius \(r\) des Abfragepunktes, wobei \(r\) ein vom Benutzer angegebener Fließkommawert ist.

Die grundlegende Nächste-Nachbarn-Regression verwendet gleichmäßige Gewichte: Das heißt, jeder Punkt in der lokalen Nachbarschaft trägt gleichmäßig zur Klassifikation eines Abfragepunktes bei. Unter bestimmten Umständen kann es vorteilhaft sein, Punkte so zu gewichten, dass nahe Punkte stärker zur Regression beitragen als weit entfernte. Dies kann durch das Schlüsselwort weights erreicht werden. Der Standardwert weights = 'uniform' weist allen Punkten gleiche Gewichte zu. weights = 'distance' weist Gewichte zu, die proportional zum Kehrwert der Distanz vom Abfragepunkt sind. Alternativ kann eine benutzerdefinierte Funktion der Distanz bereitgestellt werden, die zur Berechnung der Gewichte verwendet wird.

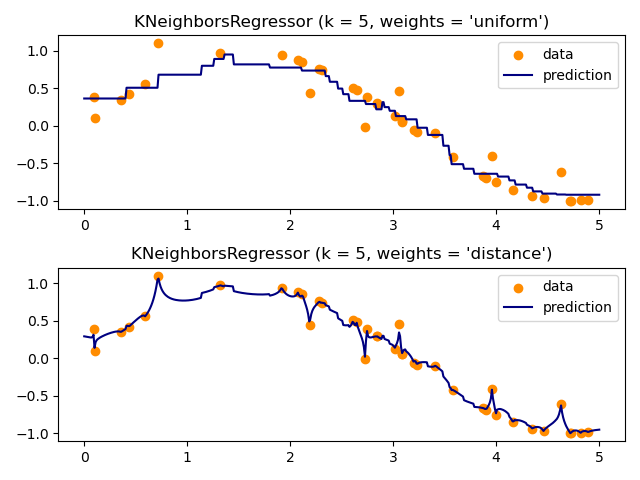
Die Verwendung von Multi-Output Nächsten Nachbarn für die Regression wird in Gesichtsergänzung mit Multi-Output-Estimators demonstriert. In diesem Beispiel sind die Eingaben X die Pixel der oberen Hälfte von Gesichtern und die Ausgaben Y die Pixel der unteren Hälfte dieser Gesichter.

Beispiele

• Regression mit Nächsten Nachbarn: ein Beispiel für Regression unter Verwendung von Nächsten Nachbarn.

• Gesichtsergänzung mit Multi-Output-Estimators: ein Beispiel für Multi-Output-Regression unter Verwendung von Nächsten Nachbarn.

1.6.4. Nächste-Nachbarn-Algorithmen

1.6.4.1. Brute Force

Die schnelle Berechnung nächster Nachbarn ist ein aktives Forschungsgebiet im maschinellen Lernen. Die naheliegendste Implementierung der Nachbarschaftssuche beinhaltet die Brute-Force-Berechnung von Distanzen zwischen allen Paaren von Punkten im Datensatz: Für \(N\) Stichproben in \(D\) Dimensionen skaliert dieser Ansatz als \(O[D N^2]\). Effiziente Brute-Force-Nachbarschaftssuchen können für kleine Datenstichproben sehr wettbewerbsfähig sein. Wenn jedoch die Anzahl der Stichproben \(N\) wächst, wird der Brute-Force-Ansatz schnell unpraktikabel. In den Klassen innerhalb von sklearn.neighbors werden Brute-Force-Nachbarschaftssuchen mit dem Schlüsselwort algorithm = 'brute' spezifiziert und mit den verfügbaren Routinen in sklearn.metrics.pairwise berechnet.

1.6.4.2. K-D-Baum

Um die rechnerischen Ineffizienzen des Brute-Force-Ansatzes zu beheben, wurden eine Vielzahl von baumbasierten Datenstrukturen erfunden. Im Allgemeinen versuchen diese Strukturen, die erforderliche Anzahl von Distanzberechnungen zu reduzieren, indem sie aggregierte Distanzinformationen für die Stichprobe effizient kodieren. Die Grundidee ist, dass wenn Punkt \(A\) sehr weit von Punkt \(B\) entfernt ist und Punkt \(B\) sehr nahe an Punkt \(C\) ist, dann wissen wir, dass die Punkte \(A\) und \(C\) sehr weit voneinander entfernt sind, ohne ihre Distanz explizit berechnen zu müssen. Auf diese Weise kann die rechnerische Kosten einer Nächste-Nachbarn-Suche auf \(O[D N \log(N)]\) oder besser reduziert werden. Dies ist eine signifikante Verbesserung gegenüber Brute Force für große \(N\).

Ein früher Ansatz, um diese aggregierten Informationen zu nutzen, war die KD-Baum-Datenstruktur (Kurzform für K-dimensionale Baum), die zwei-dimensionale Quad-Trees und drei-dimensionale Oct-Trees auf eine beliebige Anzahl von Dimensionen verallgemeinert. Der KD-Baum ist eine binäre Baumstruktur, die den Parameterraum entlang der Datenachsen rekursiv partitioniert und ihn in verschachtelte orthotope Regionen unterteilt, in die die Datenpunkte eingeordnet werden. Die Konstruktion eines KD-Baums ist sehr schnell: Da die Partitionierung nur entlang der Datenachsen erfolgt, müssen keine \(D\)-dimensionalen Distanzen berechnet werden. Nach der Konstruktion kann der nächste Nachbar eines Abfragepunktes mit nur \(O[\log(N)]\) Distanzberechnungen ermittelt werden. Obwohl der KD-Baum-Ansatz für niederdimensionale (\(D < 20\)) Nachbarschaftssuchen sehr schnell ist, wird er ineffizient, wenn \(D\) sehr groß wird: Dies ist eine Erscheinungsform des sogenannten „Fluchs der Dimensionalität“. In scikit-learn werden KD-Baum-Nachbarschaftssuchen mit dem Schlüsselwort algorithm = 'kd_tree' spezifiziert und mit der Klasse KDTree berechnet.

Referenzen

• „Multidimensional binary search trees used for associative searching“, Bentley, J.L., Communications of the ACM (1975)

1.6.4.3. Ball Tree

Um die Ineffizienzen von KD-Bäumen in höheren Dimensionen zu beheben, wurde die Ball Tree-Datenstruktur entwickelt. Während KD-Bäume Daten entlang kartesischer Achsen partitionieren, partitionieren Ball-Bäume Daten in einer Reihe von verschachtelten Hyperkugeln. Dies macht die Baumkonstruktion kostspieliger als die des KD-Baums, führt aber zu einer Datenstruktur, die auch in sehr hohen Dimensionen bei stark strukturierten Daten sehr effizient sein kann.

Ein Ball-Baum teilt die Daten rekursiv in Knoten auf, die durch einen Mittelpunkt \(C\) und einen Radius \(r\) definiert sind, so dass jeder Punkt im Knoten innerhalb der Hyperkugel liegt, die durch \(r\) und \(C\) definiert ist. Die Anzahl der Kandidatenpunkte für eine Nachbarschaftssuche wird durch die Verwendung der Dreiecksungleichung reduziert.

\[|x+y| \leq |x| + |y|\]

Mit dieser Konfiguration ist eine einzige Distanzberechnung zwischen einem Testpunkt und dem Mittelpunkt ausreichend, um eine untere und obere Schranke für die Distanz zu allen Punkten innerhalb des Knotens zu bestimmen. Aufgrund der sphärischen Geometrie der Ball-Baum-Knoten kann er in hohen Dimensionen einen KD-Baum übertreffen, obwohl die tatsächliche Leistung stark von der Struktur der Trainingsdaten abhängt. In scikit-learn werden Ball-Baum-basierte Nachbarschaftssuchen mit dem Schlüsselwort algorithm = 'ball_tree' spezifiziert und mit der Klasse BallTree berechnet. Alternativ kann der Benutzer direkt mit der Klasse BallTree arbeiten.

Referenzen

• „Five Balltree Construction Algorithms“, Omohundro, S.M., International Computer Science Institute Technical Report (1989)

Wahl des Nächste-Nachbarn-Algorithmus

Der optimale Algorithmus für einen gegebenen Datensatz ist eine komplizierte Wahl und hängt von einer Reihe von Faktoren ab.

• Anzahl der Stichproben \(N\) (d.h. n_samples) und Dimensionalität \(D\) (d.h. n_features).

  • Brute-Force-Abfragezeit wächst als \(O[D N]\)

  • Ball Tree-Abfragezeit wächst annähernd als \(O[D \log(N)]\)

  • KD Tree-Abfragezeit ändert sich mit \(D\) auf eine Weise, die schwer genau zu charakterisieren ist. Für kleines \(D\) (weniger als etwa 20) ist die Kosten annähernd \(O[D\log(N)]\), und die KD-Baum-Abfrage kann sehr effizient sein. Für größere \(D\) steigen die Kosten auf fast \(O[DN]\), und der Overhead durch die Baumstruktur kann zu Abfragen führen, die langsamer als Brute Force sind.

  Für kleine Datensätze (\(N\) kleiner als etwa 30) ist \(\log(N)\) mit \(N\) vergleichbar, und Brute-Force-Algorithmen können effizienter als baumbasierte Ansätze sein. Sowohl KDTree als auch BallTree adressieren dies, indem sie einen leaf_size-Parameter bereitstellen: dieser steuert die Anzahl der Stichproben, bei der eine Abfrage zu Brute Force wechselt. Dies ermöglicht beiden Algorithmen, die Effizienz einer Brute-Force-Berechnung für kleines \(N\) zu erreichen.

• Datenstruktur: intrinsische Dimensionalität der Daten und/oder Sparsity der Daten. Intrinsische Dimensionalität bezieht sich auf die Dimension \(d \le D\) einer Mannigfaltigkeit, auf der die Daten liegen, welche linear oder nicht-linear in den Parameterraum eingebettet sein kann. Sparsity bezieht sich auf den Grad, zu dem die Daten den Parameterraum füllen (dies ist vom Konzept der „sparsen“ Matrizen zu unterscheiden. Die Datenmatrix kann keine Nullen enthalten, aber die **Struktur** kann in diesem Sinne immer noch „sparsch“ sein).

  • Brute-Force-Abfragezeit ist unverändert durch die Datenstruktur.

  • Ball Tree und KD Tree-Abfragezeiten können durch die Datenstruktur stark beeinflusst werden. Im Allgemeinen führen sparsiere Daten mit geringerer intrinsischer Dimensionalität zu schnelleren Abfragezeiten. Da die interne Darstellung des KD-Baums auf die Parameterachsen ausgerichtet ist, wird er bei beliebig strukturierten Daten im Allgemeinen keine so große Verbesserung wie der Ball Tree zeigen.

  Datensätze, die im maschinellen Lernen verwendet werden, sind tendenziell sehr strukturiert und eignen sich sehr gut für baumbasierte Abfragen.

• Anzahl der Nachbarn \(k\), die für einen Abfragepunkt angefordert werden.

  • Brute-Force-Abfragezeit ist weitgehend unbeeinflusst vom Wert von \(k\).

  • Ball Tree und KD Tree-Abfragezeiten werden langsamer, wenn \(k\) zunimmt. Dies liegt an zwei Effekten: Erstens führt ein größeres \(k\) zur Notwendigkeit, einen größeren Teil des Parameterraums zu durchsuchen. Zweitens erfordert die Verwendung von \(k > 1\) eine interne Warteschlangenerstellung von Ergebnissen, während der Baum durchlaufen wird.

  Wenn \(k\) groß im Vergleich zu \(N\) wird, wird die Fähigkeit, Äste in einer baumbasierten Abfrage zu beschneiden, reduziert. In dieser Situation können Brute-Force-Abfragen effizienter sein.

• Anzahl der Abfragepunkte. Sowohl der Ball Tree als auch der KD Tree erfordern eine Konstruktionsphase. Die Kosten dieser Konstruktion werden bei Mehrfachabfragen vernachlässigbar. Wenn nur eine geringe Anzahl von Abfragen durchgeführt wird, macht die Konstruktion jedoch einen erheblichen Teil der Gesamtkosten aus. Wenn nur sehr wenige Abfragepunkte benötigt werden, ist Brute Force besser als eine baumbasierte Methode.

Derzeit wählt algorithm = 'auto' 'brute', wenn eine der folgenden Bedingungen erfüllt ist:

• Eingabedaten sind sparsen.

• metric = 'precomputed'

• \(D > 15\)

• \(k >= N/2\)

• effective_metric_ ist nicht in der Liste VALID_METRICS für 'kd_tree' oder 'ball_tree'.

Andernfalls wählt er den ersten aus 'kd_tree' und 'ball_tree', für den effective_metric_ in seiner Liste VALID_METRICS enthalten ist. Diese Heuristik basiert auf folgenden Annahmen:

• Die Anzahl der Abfragepunkte ist mindestens von der gleichen Größenordnung wie die Anzahl der Trainingspunkte.

• leaf_size liegt nahe seinem Standardwert von 30.

• Wenn \(D > 15\), ist die intrinsische Dimensionalität der Daten im Allgemeinen zu hoch für baumbasierte Methoden.

Auswirkung von leaf_size

Wie oben erwähnt, kann für kleine Stichprobengrößen eine Brute-Force-Suche effizienter sein als eine baumbasierte Abfrage. Diese Tatsache wird im Ball Tree und KD Tree berücksichtigt, indem intern zu Brute-Force-Suchen innerhalb der Blattknoten gewechselt wird. Die Ebene dieses Wechsels kann mit dem Parameter leaf_size festgelegt werden. Die Wahl dieses Parameters hat viele Auswirkungen:

Konstruktionszeit

Ein größerer leaf_size führt zu einer schnelleren Baumkonstruktionszeit, da weniger Knoten erstellt werden müssen.

Abfragezeit

Sowohl eine große als auch eine kleine leaf_size können zu suboptimalen Abfragekosten führen. Bei leaf_size nahe 1 können die Overheadkosten für das Durchlaufen von Knoten die Abfragezeiten erheblich verlangsamen. Bei leaf_size nahe der Größe des Trainingsdatensatzes werden Abfragen im Wesentlichen zu Brute-Force. Ein guter Kompromiss zwischen diesen ist leaf_size = 30, der Standardwert des Parameters.

Speicher

Mit zunehmender leaf_size nimmt der Speicherbedarf für die Speicherung einer Baumstruktur ab. Dies ist besonders wichtig im Fall des Ball Tree, der für jeden Knoten einen \(D\)-dimensionalen Mittelpunkt speichert. Der benötigte Speicherplatz für BallTree beträgt ungefähr das 1 / leaf_size-fache der Größe des Trainingsdatensatzes.

leaf_size wird für Brute-Force-Abfragen nicht referenziert.

Gültige Metriken für Nächste-Nachbarn-Algorithmen

Für eine Liste verfügbarer Metriken siehe die Dokumentation der Klasse DistanceMetric und die in sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS aufgeführten Metriken. Beachten Sie, dass die Metrik „cosine“ cosine_distances verwendet.

Eine Liste gültiger Metriken für alle oben genannten Algorithmen kann über deren Attribut valid_metric abgerufen werden. Zum Beispiel können gültige Metriken für KDTree wie folgt generiert werden:

>>> from sklearn.neighbors import KDTree
>>> print(sorted(KDTree.valid_metrics))
['chebyshev', 'cityblock', 'euclidean', 'infinity', 'l1', 'l2', 'manhattan', 'minkowski', 'p']

1.6.5. Nearest Centroid Classifier

Der Klassifikator NearestCentroid ist ein einfacher Algorithmus, der jede Klasse durch den Schwerpunkt ihrer Mitglieder repräsentiert. Dies macht ihn effektiv ähnlich der Label-Aktualisierungsphase des Algorithmus KMeans. Er hat auch keine zu wählenden Parameter, was ihn zu einem guten Basisklassifikator macht. Allerdings hat er Nachteile bei nicht-konvexen Klassen und wenn Klassen drastisch unterschiedliche Varianzen aufweisen, da gleiche Varianz in allen Dimensionen angenommen wird. Siehe Lineare Diskriminanzanalyse (LinearDiscriminantAnalysis) und Quadratische Diskriminanzanalyse (QuadraticDiscriminantAnalysis) für komplexere Methoden, die diese Annahme nicht treffen. Die Verwendung des Standard-NearestCentroid ist einfach.

>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]

1.6.5.1. Nearest Shrunken Centroid

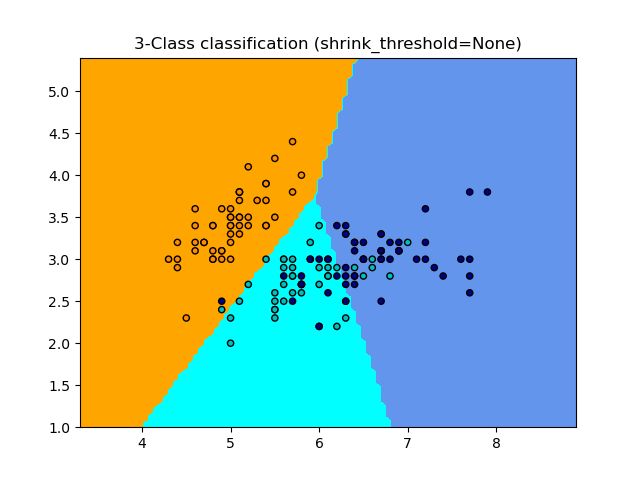
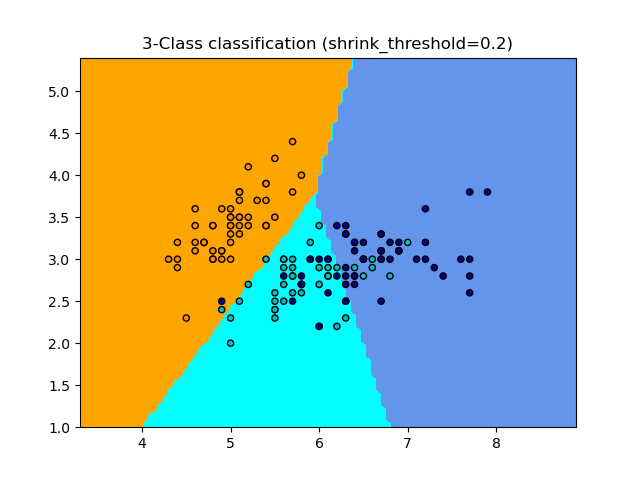
Der Klassifikator NearestCentroid verfügt über den Parameter shrink_threshold, der den Nearest Shrunken Centroid-Klassifikator implementiert. Tatsächlich wird der Wert jeder Merkmalsspalte für jeden Schwerpunkt durch die Varianz innerhalb der Klasse dieses Merkmals geteilt. Die Merkmalswerte werden dann um shrink_threshold reduziert. Insbesondere wenn ein bestimmter Merkmalswert Null überschreitet, wird er auf Null gesetzt. Dies führt dazu, dass das Merkmal die Klassifizierung nicht mehr beeinflusst. Dies ist beispielsweise nützlich, um verrauschte Merkmale zu entfernen.

Im folgenden Beispiel erhöht die Verwendung eines kleinen Schwellenwerts für die Schrumpfung die Genauigkeit des Modells von 0,81 auf 0,82.

Beispiele

• Nearest Centroid Classification: Ein Beispiel für die Klassifizierung mit Nearest Centroid mit verschiedenen Schrumpfungsschwellen.

1.6.6. Nearest Neighbors Transformer

Viele scikit-learn-Schätzer basieren auf Nearest Neighbors: Mehrere Klassifikatoren und Regressoren wie KNeighborsClassifier und KNeighborsRegressor, aber auch einige Clustering-Methoden wie DBSCAN und SpectralClustering, sowie einige Mannigfaltigkeits-Einbettungen wie TSNE und Isomap.

All diese Schätzer können intern die nächsten Nachbarn berechnen, aber die meisten akzeptieren auch vorberechnete nächste Nachbarn dünne Graphen, wie sie von kneighbors_graph und radius_neighbors_graph bereitgestellt werden. Mit dem Modus mode='connectivity' geben diese Funktionen einen binären dünnen Adjazenzgraphen zurück, wie er beispielsweise für SpectralClustering benötigt wird. Während sie mit mode='distance' einen dünnen Distanzgraphen zurückgeben, wie er beispielsweise für DBSCAN benötigt wird. Um diese Funktionen in eine scikit-learn-Pipeline aufzunehmen, kann man auch die entsprechenden Klassen KNeighborsTransformer und RadiusNeighborsTransformer verwenden. Die Vorteile dieser dünnen Graphen-API sind vielfältig.

Erstens kann der vorberechnete Graph mehrmals wiederverwendet werden, zum Beispiel beim Variieren eines Parameters des Schätzers. Dies kann manuell vom Benutzer oder unter Nutzung der Caching-Eigenschaften der scikit-learn-Pipeline erfolgen.

>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir()  # we use a temporary folder here
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
...     KNeighborsTransformer(mode='distance'),
...     Isomap(n_components=3, metric='precomputed'),
...     memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)

Zweitens kann die Vorberechnung des Graphen eine feinere Kontrolle über die Schätzung der nächsten Nachbarn ermöglichen, beispielsweise durch Aktivierung von Multiprocessing über den Parameter n_jobs, der möglicherweise nicht in allen Schätzern verfügbar ist.

Schließlich kann die Vorberechnung durch benutzerdefinierte Schätzer erfolgen, um unterschiedliche Implementierungen zu verwenden, wie z. B. approximative Nearest-Neighbors-Methoden oder Implementierungen mit speziellen Datentypen. Der vorberechnete Nachbar-dünne Graph muss wie in der Ausgabe von radius_neighbors_graph formatiert sein.

• eine CSR-Matrix (obwohl auch COO, CSC oder LIL akzeptiert werden).

• nur explizit die nächsten Nachbarschaften jedes Samples in Bezug auf die Trainingsdaten speichern. Dies sollte auch solche umfassen, die eine Distanz von 0 zu einem Abfragepunkt haben, einschließlich der Matrixdiagonalen, wenn die nächsten Nachbarschaften zwischen den Trainingsdaten und sich selbst berechnet werden.

• die data jeder Zeile sollte die Distanzen in aufsteigender Reihenfolge enthalten (optional. Unsotierte Daten werden stabil sortiert, was einen zusätzlichen Rechenaufwand bedeutet).

• alle Werte in data sollten nicht negativ sein.

• es sollte keine doppelten indices in einer Zeile geben (siehe scipy/scipy#5807).

• Wenn der Algorithmus, dem die vorberechnete Matrix übergeben wird, k nächste Nachbarn verwendet (im Gegensatz zu Radius-Nachbarschaften), müssen in jeder Zeile mindestens k Nachbarn gespeichert werden (oder k+1, wie in der folgenden Anmerkung erklärt).

Hinweis

Wenn eine bestimmte Anzahl von Nachbarn abgefragt wird (unter Verwendung von KNeighborsTransformer), ist die Definition von n_neighbors mehrdeutig, da sie entweder jeden Trainingspunkt als seinen eigenen Nachbarn einschließen oder ausschließen kann. Keine der beiden Entscheidungen ist perfekt, da das Einschließen zu einer unterschiedlichen Anzahl von Nicht-Selbst-Nachbarn während des Trainings und Testens führt, während das Ausschließen zu einem Unterschied zwischen fit(X).transform(X) und fit_transform(X) führt, was gegen die scikit-learn-API verstößt. In KNeighborsTransformer verwenden wir die Definition, die jeden Trainingspunkt als seinen eigenen Nachbarn in die Zählung von n_neighbors einschließt. Aus Kompatibilitätsgründen mit anderen Schätzern, die die andere Definition verwenden, wird jedoch ein zusätzlicher Nachbar berechnet, wenn mode == 'distance'. Um die Kompatibilität mit allen Schätzern zu maximieren, ist eine sichere Wahl, immer einen zusätzlichen Nachbarn in einem benutzerdefinierten Nearest-Neighbors-Schätzer einzuschließen, da unnötige Nachbarn von nachfolgenden Schätzern gefiltert werden.

Beispiele

• Approximate nearest neighbors in TSNE: Ein Beispiel für die Verknüpfung von KNeighborsTransformer und TSNE. Bietet auch zwei benutzerdefinierte Nearest-Neighbors-Schätzer, die auf externen Paketen basieren.

• Caching nearest neighbors: Ein Beispiel für die Verknüpfung von KNeighborsTransformer und KNeighborsClassifier zur Aktivierung des Cachings des Nachbargraphen während einer Hyperparameter-Grid-Suche.

1.6.7. Neighborhood Components Analysis

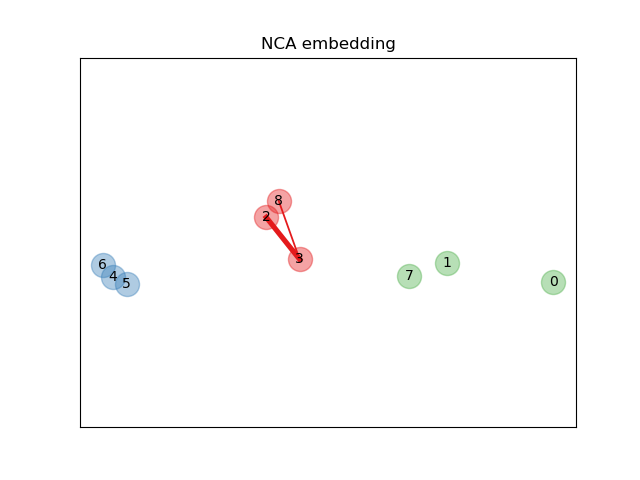
Neighborhood Components Analysis (NCA, NeighborhoodComponentsAnalysis) ist ein Algorithmus zum Lernen von Distanzmetriken, der darauf abzielt, die Genauigkeit der Klassifizierung durch Nearest Neighbors im Vergleich zur Standard-Euklidischen Distanz zu verbessern. Der Algorithmus maximiert direkt eine stochastische Variante des Leave-One-Out k-Nearest Neighbors (KNN) Scores auf dem Trainingsdatensatz. Er kann auch einen niedrigdimensionalen linearen Projektionsraum für Daten lernen, der für die Datenvisualisierung und schnelle Klassifizierung verwendet werden kann.

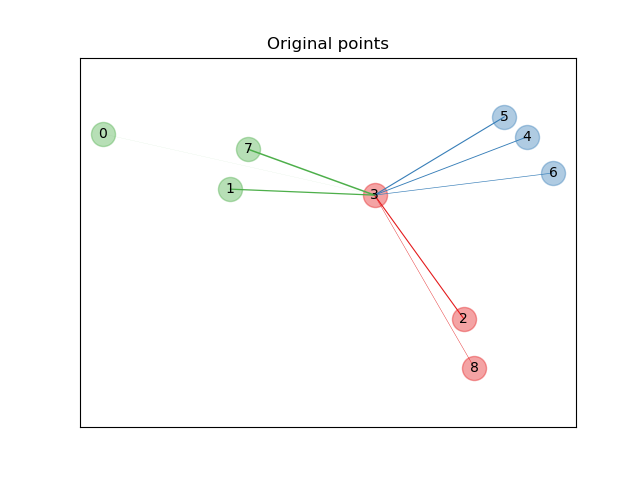
In der obigen illustrierenden Abbildung betrachten wir einige Punkte aus einem zufällig generierten Datensatz. Wir konzentrieren uns auf die stochastische KNN-Klassifizierung von Punkt Nr. 3. Die Dicke einer Verbindung zwischen Stichprobe 3 und einem anderen Punkt ist proportional zu ihrer Distanz und kann als relatives Gewicht (oder Wahrscheinlichkeit) gesehen werden, das eine stochastische Nearest-Neighbor-Vorhersageregel diesem Punkt zuweisen würde. Im ursprünglichen Raum hat Stichprobe 3 viele stochastische Nachbarn aus verschiedenen Klassen, sodass die richtige Klasse nicht sehr wahrscheinlich ist. Im durch NCA gelernten projizierten Raum sind jedoch die einzigen stochastischen Nachbarn mit nicht vernachlässigbarem Gewicht aus der gleichen Klasse wie Stichprobe 3, was garantiert, dass letztere gut klassifiziert wird. Siehe die mathematische Formulierung für weitere Details.

1.6.7.1. Classification

In Kombination mit einem Nearest-Neighbors-Klassifikator (KNeighborsClassifier) ist NCA attraktiv für die Klassifizierung, da es natürlich Mehrklassenprobleme ohne Vergrößerung der Modellgröße verarbeiten kann und keine zusätzlichen Parameter einführt, die vom Benutzer feinjustiert werden müssen.

Die NCA-Klassifizierung hat sich in der Praxis als gut funktionierend für Datensätze unterschiedlicher Größe und Schwierigkeitsgrade erwiesen. Im Gegensatz zu verwandten Methoden wie der Linearen Diskriminanzanalyse trifft NCA keine Annahmen über die Klassenverteilungen. Die Nearest-Neighbor-Klassifizierung kann natürlich stark unregelmäßige Entscheidungsgrenzen erzeugen.

Um dieses Modell für die Klassifizierung zu verwenden, muss eine Instanz von NeighborhoodComponentsAnalysis, die die optimale Transformation lernt, mit einer Instanz von KNeighborsClassifier kombiniert werden, die die Klassifizierung im projizierten Raum durchführt. Hier ist ein Beispiel, das die beiden Klassen verwendet.

>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...

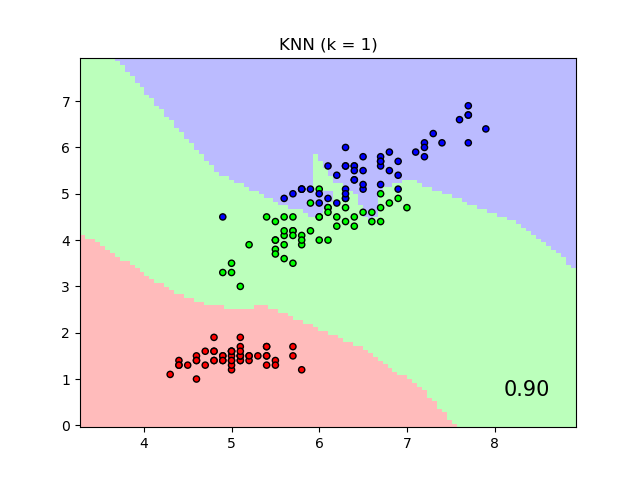
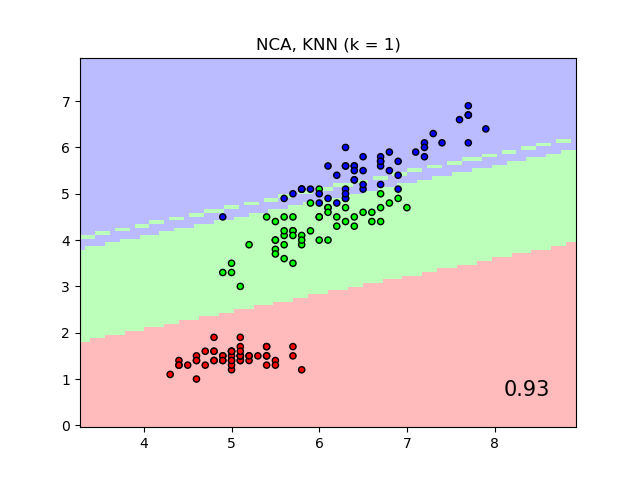
Die Darstellung zeigt die Entscheidungsgrenzen für die Nearest Neighbor Classification und die Neighborhood Components Analysis Classification auf dem Iris-Datensatz, wobei für Visualisierungszwecke nur auf zwei Merkmale trainiert und bewertet wird.

1.6.7.2. Dimensionality reduction

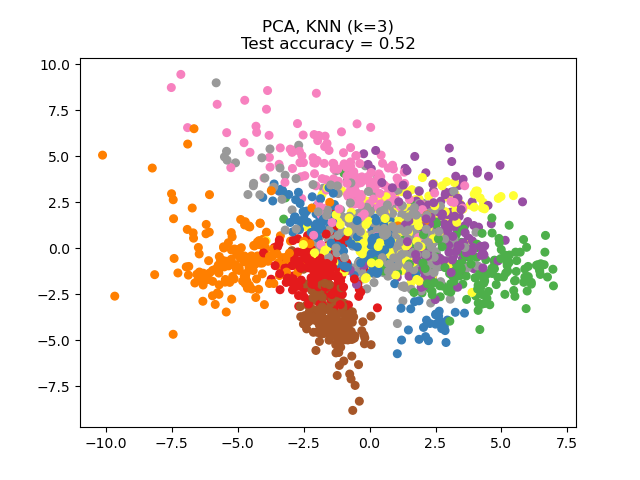
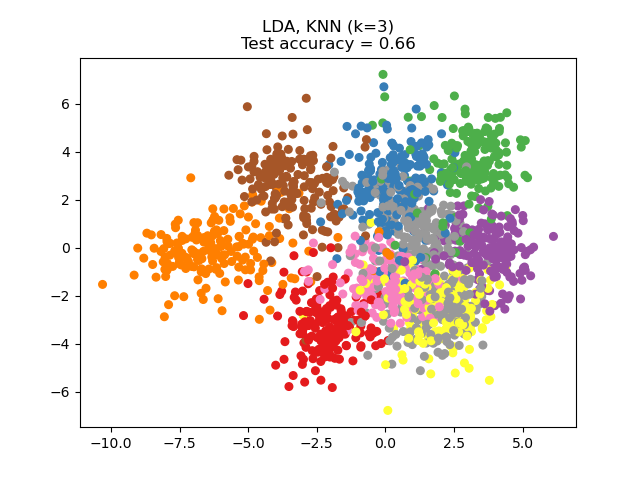
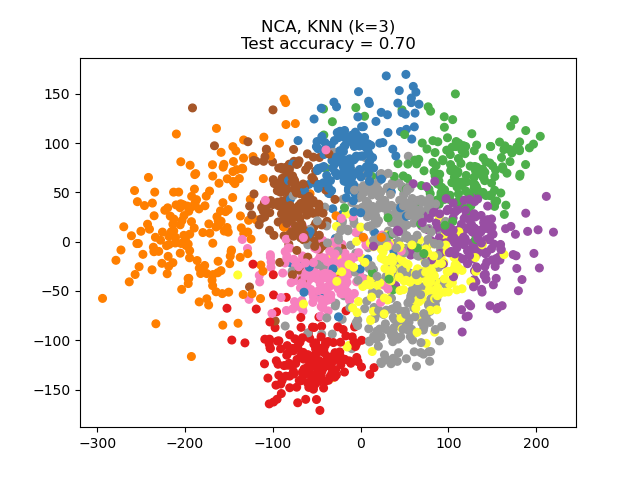
NCA kann zur überwachten Dimensionsreduktion verwendet werden. Die Eingabedaten werden auf einen linearen Unterraum projiziert, der aus den Richtungen besteht, die das NCA-Ziel minimieren. Die gewünschte Dimensionalität kann mit dem Parameter n_components eingestellt werden. Beispielsweise zeigt die folgende Abbildung einen Vergleich der Dimensionsreduktion mit Principal Component Analysis (PCA), Linear Discriminant Analysis (LinearDiscriminantAnalysis) und Neighborhood Component Analysis (NeighborhoodComponentsAnalysis) auf dem Digits-Datensatz, einem Datensatz mit der Größe \(n_{samples} = 1797\) und \(n_{features} = 64\). Der Datensatz wird in gleich große Trainings- und Testdatensätze aufgeteilt und standardisiert. Zur Auswertung wird die 3-Nearest-Neighbor-Klassifikationsgenauigkeit auf den 2-dimensionalen projizierten Punkten berechnet, die von jeder Methode gefunden wurden. Jeder Datenpunkt gehört zu einer von 10 Klassen.

Beispiele

• Vergleich von Nächsten Nachbarn mit und ohne Neighborhood Components Analysis

• Dimensionsreduktion mit Neighborhood Components Analysis

• Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

1.6.7.3. Mathematical formulation

Ziel von NCA ist es, eine optimale lineare Transformationsmatrix der Größe (n_components, n_features) zu lernen, die die Summe über alle Stichproben \(i\) der Wahrscheinlichkeit \(p_i\) maximiert, dass \(i\) korrekt klassifiziert wird, d. h.

\[\underset{L}{\arg\max} \sum\limits_{i=0}^{N - 1} p_{i}\]

mit \(N\) = n_samples und \(p_i\) der Wahrscheinlichkeit, dass Stichprobe \(i\) gemäß einer stochastischen Nearest-Neighbors-Regel im gelernten eingebetteten Raum korrekt klassifiziert wird.

\[p_{i}=\sum\limits_{j \in C_i}{p_{i j}}\]

wobei \(C_i\) die Menge der Punkte in der gleichen Klasse wie Stichprobe \(i\) ist und \(p_{i j}\) der Softmax über euklidische Distanzen im eingebetteten Raum ist.

\[p_{i j} = \frac{\exp(-||L x_i - L x_j||^2)}{\sum\limits_{k \ne i} {\exp{-(||L x_i - L x_k||^2)}}} , \quad p_{i i} = 0\]

Mahalanobis distance

NCA kann als das Lernen einer (quadratischen) Mahalanobis-Distanzmetrik betrachtet werden.

\[|| L(x_i - x_j)||^2 = (x_i - x_j)^TM(x_i - x_j),\]

wobei \(M = L^T L\) eine symmetrische, positiv semidefinitive Matrix der Größe (n_features, n_features) ist.

1.6.7.4. Implementation

Diese Implementierung folgt dem, was im Originalpapier [1] erläutert wird. Für die Optimierungsmethode wird derzeit scipy's L-BFGS-B mit einer vollständigen Gradientenberechnung bei jeder Iteration verwendet, um die Lernrate nicht einstellen zu müssen und ein stabiles Lernen zu gewährleisten.

Siehe die folgenden Beispiele und die Docstring von NeighborhoodComponentsAnalysis.fit für weitere Informationen.

1.6.7.5. Complexity

1.6.7.5.1. Training

NCA speichert eine Matrix paarweiser Distanzen, was n_samples ** 2 Speicherplatz benötigt. Die Zeitkomplexität hängt von der Anzahl der Iterationen ab, die vom Optimierungsalgorithmus durchgeführt werden. Man kann jedoch die maximale Anzahl von Iterationen mit dem Argument max_iter festlegen. Für jede Iteration beträgt die Zeitkomplexität O(n_components x n_samples x min(n_samples, n_features)).

1.6.7.5.2. Transform

Hier gibt die transform Operation \(LX^T\) zurück, daher entspricht ihre Zeitkomplexität n_components * n_features * n_samples_test. Es gibt keine zusätzliche Raumkomplexität bei der Operation.

Referenzen

[1]

„Neighbourhood Components Analysis“, J. Goldberger, S. Roweis, G. Hinton, R. Salakhutdinov, Advances in Neural Information Processing Systems, Vol. 17, Mai 2005, S. 513-520.

• Wikipedia-Eintrag zu Neighborhood Components Analysis