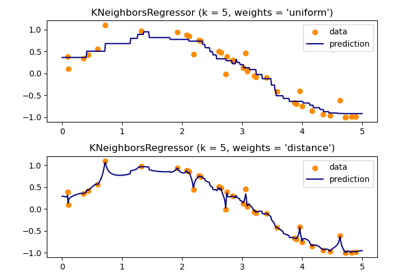
KNeighborsRegressor#
- class sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)[Quelle]#
Regression basierend auf k-nächsten Nachbarn.
Das Ziel wird durch lokale Interpolation der Ziele der nächsten Nachbarn im Trainingsdatensatz vorhergesagt.
Lesen Sie mehr im Benutzerhandbuch.
Hinzugefügt in Version 0.9.
- Parameter:
- n_neighborsint, Standard=5
Anzahl der standardmäßig für
kneighbors-Abfragen zu verwendenden Nachbarn.- weights{‘uniform’, ‘distance’}, aufrufbar oder None, Standard=’uniform’
Gewichtsfunktion, die bei der Vorhersage verwendet wird. Mögliche Werte
‘uniform’ : gleichmäßige Gewichte. Alle Punkte in jedem Nachbarschaftsbereich werden gleich gewichtet.
‘distance’ : Punkte werden nach dem Kehrwert ihrer Entfernung gewichtet. In diesem Fall haben nähere Nachbarn eines Anfragepunkts mehr Einfluss als weiter entfernte Nachbarn.
[aufrufbar] : eine benutzerdefinierte Funktion, die ein Array von Entfernungen akzeptiert und ein Array derselben Form mit den Gewichten zurückgibt.
Gleichmäßige Gewichte werden standardmäßig verwendet.
Siehe das folgende Beispiel für eine Demonstration der Auswirkungen verschiedener Gewichtungsschemata auf Vorhersagen: Nearest Neighbors Regression.
- algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, Standard=’auto’
Algorithmus zur Berechnung der nächsten Nachbarn
‘ball_tree’ verwendet
BallTree‘kd_tree’ verwendet
KDTree‘brute’ verwendet eine brute-force Suche.
„auto“ versucht, den am besten geeigneten Algorithmus basierend auf den an die
fit-Methode übergebenen Werten zu ermitteln.
Hinweis: Das Anpassen an dünnbesetzte Eingaben überschreibt die Einstellung dieses Parameters und verwendet brute force.
- leaf_sizeint, Standard=30
Anzahl der Blätter, die an BallTree oder KDTree übergeben werden. Dies kann die Geschwindigkeit des Aufbaus und der Abfrage sowie den benötigten Speicherplatz für den Baum beeinflussen. Der optimale Wert hängt von der Art des Problems ab.
- pfloat, Standard=2
Potenzparameter für die Minkowski-Metrik. Wenn p = 1 ist, ist dies äquivalent zur Verwendung von manhattan_distance (l1) und euclidean_distance (l2) für p = 2. Für beliebige p wird minkowski_distance (l_p) verwendet.
- metricstr, DistanceMetric-Objekt oder aufrufbar, Standard='minkowski'
Metrik zur Entfernungsberechnung. Standard ist „minkowski“, was bei p = 2 zur Standard-Euklidischen Distanz führt. Siehe die Dokumentation von scipy.spatial.distance und die unter
distance_metricsaufgeführten Metriken für gültige Metrikwerte.Wenn metric “precomputed” ist, wird davon ausgegangen, dass X eine Distanzmatrix ist und während des Anlernens quadratisch sein muss. X kann ein dünnbesetzter Graph sein, in diesem Fall können nur “nonzero” Elemente als Nachbarn betrachtet werden.
Wenn metric eine aufrufbare Funktion ist, nimmt sie zwei Arrays entgegen, die 1D-Vektoren darstellen, und muss einen Wert zurückgeben, der die Entfernung zwischen diesen Vektoren angibt. Dies funktioniert für Scipys Metriken, ist aber weniger effizient als die Übergabe des Metriknamens als String.
Wenn metric ein DistanceMetric-Objekt ist, wird es direkt an die zugrunde liegenden Berechnungsroutinen übergeben.
- metric_paramsdict, Standard=None
Zusätzliche Schlüsselwortargumente für die Metrikfunktion.
- n_jobsint, default=None
Die Anzahl der parallelen Jobs, die für die Nachbarschaftssuche ausgeführt werden.
Nonebedeutet 1, es sei denn, es befindet sich in einemjoblib.parallel_backend-Kontext.-1bedeutet die Verwendung aller Prozessoren. Weitere Details finden Sie im Glossar. Beeinflusst diefit-Methode nicht.
- Attribute:
- effective_metric_str oder callable
Die zu verwendende Distanzmetrik. Sie ist identisch mit dem Parameter
metricoder ein Synonym dafür, z. B. ‚euclidean‘, wenn der Parametermetricauf ‚minkowski‘ und der Parameterpauf 2 gesetzt ist.- effective_metric_params_dict
Zusätzliche Schlüsselwortargumente für die Metrikfunktion. Für die meisten Metriken ist dies dasselbe wie der Parameter
metric_params, kann aber auch den Wert des Parameterspenthalten, wenn das Attributeffective_metric_auf ‘minkowski’ gesetzt ist.- n_features_in_int
Anzahl der während des fits gesehenen Merkmale.
Hinzugefügt in Version 0.24.
- feature_names_in_ndarray mit Form (
n_features_in_,) Namen der während fit gesehenen Merkmale. Nur definiert, wenn
XMerkmalnamen hat, die alle Zeichenketten sind.Hinzugefügt in Version 1.0.
- n_samples_fit_int
Anzahl der Samples in den angepassten Daten.
Siehe auch
NearestNeighborsUnüberwachter Lerner zur Implementierung von Nachbarschaftssuchen.
RadiusNeighborsRegressorRegression basierend auf Nachbarn innerhalb eines festen Radius.
KNeighborsClassifierKlassifikator, der die k-nächste-Nachbarn-Abstimmung implementiert.
RadiusNeighborsClassifierKlassifikator, der eine Abstimmung unter Nachbarn innerhalb eines gegebenen Radius implementiert.
Anmerkungen
Siehe Nearest Neighbors in der Online-Dokumentation für eine Diskussion der Wahl von
algorithmundleaf_size.Warnung
In Bezug auf die Nearest Neighbors-Algorithmen hängt das Ergebnis davon ab, wie die Trainingsdaten sortiert sind, wenn festgestellt wird, dass zwei Nachbarn, Nachbar
k+1undk, identische Distanzen, aber unterschiedliche Labels haben.https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm
Beispiele
>>> X = [[0], [1], [2], [3]] >>> y = [0, 0, 1, 1] >>> from sklearn.neighbors import KNeighborsRegressor >>> neigh = KNeighborsRegressor(n_neighbors=2) >>> neigh.fit(X, y) KNeighborsRegressor(...) >>> print(neigh.predict([[1.5]])) [0.5]
- fit(X, y)[Quelle]#
Passt den k-nearest neighbors Regressor aus dem Trainingsdatensatz an.
- Parameter:
- X{array-like, sparse matrix} der Form (n_samples, n_features) oder (n_samples, n_samples), wenn metric=’precomputed’
Trainingsdaten.
- y{array-like, sparse matrix} der Form (n_samples,) oder (n_samples, n_outputs)
Zielwerte.
- Gibt zurück:
- selfKNeighborsRegressor
Der angepasste k-nearest neighbors Regressor.
- get_metadata_routing()[Quelle]#
Holt das Metadaten-Routing dieses Objekts.
Bitte prüfen Sie im Benutzerhandbuch, wie der Routing-Mechanismus funktioniert.
- Gibt zurück:
- routingMetadataRequest
Ein
MetadataRequest, der Routing-Informationen kapselt.
- get_params(deep=True)[Quelle]#
Holt Parameter für diesen Schätzer.
- Parameter:
- deepbool, default=True
Wenn True, werden die Parameter für diesen Schätzer und die enthaltenen Unterobjekte, die Schätzer sind, zurückgegeben.
- Gibt zurück:
- paramsdict
Parameternamen, zugeordnet ihren Werten.
- kneighbors(X=None, n_neighbors=None, return_distance=True)[Quelle]#
Finde die K-Nachbarn eines Punktes.
Gibt Indizes von und Entfernungen zu den Nachbarn jedes Punktes zurück.
- Parameter:
- X{array-like, sparse matrix}, Form (n_queries, n_features) oder (n_queries, n_indexed), wenn metric == ‘precomputed’, Standard=None
Der Anfragepunkt oder die Anfragepunkte. Wenn nicht angegeben, werden die Nachbarn jedes indizierten Punktes zurückgegeben. In diesem Fall wird der Anfragepunkt nicht als sein eigener Nachbar betrachtet.
- n_neighborsint, Standard=None
Anzahl der für jede Stichprobe erforderlichen Nachbarn. Der Standardwert ist der Wert, der an den Konstruktor übergeben wurde.
- return_distancebool, Standard=True
Gibt zurück, ob die Entfernungen zurückgegeben werden sollen.
- Gibt zurück:
- neigh_distndarray der Form (n_queries, n_neighbors)
Array, das die Längen zu den Punkten darstellt, nur vorhanden, wenn return_distance=True.
- neigh_indndarray der Form (n_queries, n_neighbors)
Indizes der nächsten Punkte in der Populationsmatrix.
Beispiele
Im folgenden Beispiel konstruieren wir eine NearestNeighbors-Klasse aus einem Array, das unser Datensatz repräsentiert, und fragen, wer der nächste Punkt zu [1,1,1] ist.
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=1) >>> neigh.fit(samples) NearestNeighbors(n_neighbors=1) >>> print(neigh.kneighbors([[1., 1., 1.]])) (array([[0.5]]), array([[2]]))
Wie Sie sehen können, gibt es [[0.5]] und [[2]] zurück, was bedeutet, dass das Element in der Entfernung 0.5 liegt und das dritte Element von samples ist (Indizes beginnen bei 0). Sie können auch mehrere Punkte abfragen.
>>> X = [[0., 1., 0.], [1., 0., 1.]] >>> neigh.kneighbors(X, return_distance=False) array([[1], [2]]...)
- kneighbors_graph(X=None, n_neighbors=None, mode='connectivity')[Quelle]#
Berechnet den (gewichteten) Graphen von k-Nachbarn für Punkte in X.
- Parameter:
- X{array-like, sparse matrix} der Form (n_queries, n_features) oder (n_queries, n_indexed), wenn metric == ‘precomputed’, Standard=None
Der Anfragepunkt oder die Anfragepunkte. Wenn nicht angegeben, werden die Nachbarn jedes indizierten Punktes zurückgegeben. In diesem Fall wird der Anfragepunkt nicht als sein eigener Nachbar betrachtet. Für
metric='precomputed'sollte die Form (n_queries, n_indexed) sein. Andernfalls sollte die Form (n_queries, n_features) sein.- n_neighborsint, Standard=None
Anzahl der Nachbarn für jede Stichprobe. Der Standardwert ist der Wert, der an den Konstruktor übergeben wurde.
- mode{‘connectivity’, ‘distance’}, Standard=’connectivity’
Typ der zurückgegebenen Matrix: ‘connectivity’ gibt die Konnektivitätsmatrix mit Einsen und Nullen zurück, bei ‘distance’ sind die Kanten die Entfernungen zwischen den Punkten; die Art der Distanz hängt vom ausgewählten Metrikparameter in der NearestNeighbors-Klasse ab.
- Gibt zurück:
- Asparse-matrix der Form (n_queries, n_samples_fit)
n_samples_fitist die Anzahl der Samples in den angepassten Daten.A[i, j]gibt das Gewicht der Kante an, dieimitjverbindet. Die Matrix hat das CSR-Format.
Siehe auch
NearestNeighbors.radius_neighbors_graphBerechnet den (gewichteten) Graphen von Nachbarn für Punkte in X.
Beispiele
>>> X = [[0], [3], [1]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=2) >>> neigh.fit(X) NearestNeighbors(n_neighbors=2) >>> A = neigh.kneighbors_graph(X) >>> A.toarray() array([[1., 0., 1.], [0., 1., 1.], [1., 0., 1.]])
- predict(X)[Quelle]#
Sagt das Ziel für die bereitgestellten Daten voraus.
- Parameter:
- X{array-like, sparse matrix} der Form (n_queries, n_features), oder (n_queries, n_indexed), wenn metric == ‘precomputed’, oder None
Teststichproben. Wenn
None, werden Vorhersagen für alle indizierten Punkte zurückgegeben; in diesem Fall werden Punkte nicht als ihre eigenen Nachbarn betrachtet.
- Gibt zurück:
- yndarray der Form (n_queries,) oder (n_queries, n_outputs), dtype=int
Zielwerte.
- score(X, y, sample_weight=None)[Quelle]#
Gibt den Bestimmtheitskoeffizienten auf Testdaten zurück.
Der Bestimmtheitskoeffizient \(R^2\) ist definiert als \((1 - \frac{u}{v})\), wobei \(u\) die Summe der quadrierten Residuen ist
((y_true - y_pred)** 2).sum()und \(v\) die Summe der quadrierten Abweichungen vom Mittelwert ist((y_true - y_true.mean()) ** 2).sum(). Der bestmögliche Score ist 1,0 und er kann negativ sein (da das Modell beliebig schlechter sein kann). Ein konstantes Modell, das immer den Erwartungswert vonyvorhersagt, ohne die Eingabemerkmale zu berücksichtigen, würde einen \(R^2\)-Score von 0,0 erhalten.- Parameter:
- Xarray-like der Form (n_samples, n_features)
Teststichproben. Für einige Schätzer kann dies eine vorab berechnete Kernelmatrix oder eine Liste von generischen Objekten sein, stattdessen mit der Form
(n_samples, n_samples_fitted), wobein_samples_fitteddie Anzahl der für die Anpassung des Schätzers verwendeten Stichproben ist.- yarray-like der Form (n_samples,) oder (n_samples, n_outputs)
Wahre Werte für
X.- sample_weightarray-like der Form (n_samples,), Standardwert=None
Stichprobengewichte.
- Gibt zurück:
- scorefloat
\(R^2\) von
self.predict(X)bezogen aufy.
Anmerkungen
Der \(R^2\)-Score, der beim Aufrufen von
scoreauf einem Regressor verwendet wird, nutzt ab Version 0.23multioutput='uniform_average', um konsistent mit dem Standardwert vonr2_scorezu sein. Dies beeinflusst diescore-Methode aller Multioutput-Regressoren (mit Ausnahme vonMultiOutputRegressor).
- set_params(**params)[Quelle]#
Setzt die Parameter dieses Schätzers.
Die Methode funktioniert sowohl bei einfachen Schätzern als auch bei verschachtelten Objekten (wie
Pipeline). Letztere haben Parameter der Form<component>__<parameter>, so dass es möglich ist, jede Komponente eines verschachtelten Objekts zu aktualisieren.- Parameter:
- **paramsdict
Schätzer-Parameter.
- Gibt zurück:
- selfestimator instance
Schätzer-Instanz.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KNeighborsRegressor[Quelle]#
Konfiguriert, ob Metadaten für die
score-Methode angefordert werden sollen.Beachten Sie, dass diese Methode nur relevant ist, wenn dieser Schätzer als Unter-Schätzer innerhalb eines Meta-Schätzers verwendet wird und Metadaten-Routing mit
enable_metadata_routing=Trueaktiviert ist (siehesklearn.set_config). Bitte lesen Sie das Benutzerhandbuch, um zu erfahren, wie der Routing-Mechanismus funktioniert.Die Optionen für jeden Parameter sind
True: Metadaten werden angefordert und, falls vorhanden, anscoreübergeben. Die Anforderung wird ignoriert, wenn keine Metadaten vorhanden sind.False: Metadaten werden nicht angefordert und der Meta-Schätzer übergibt sie nicht anscore.None: Metadaten werden nicht angefordert und der Meta-Schätzer löst einen Fehler aus, wenn der Benutzer sie bereitstellt.str: Metadaten sollten mit diesem Alias an den Meta-Schätzer übergeben werden und nicht mit dem ursprünglichen Namen.
Der Standardwert (
sklearn.utils.metadata_routing.UNCHANGED) behält die bestehende Anforderung bei. Dies ermöglicht es Ihnen, die Anforderung für einige Parameter zu ändern und für andere nicht.Hinzugefügt in Version 1.3.
- Parameter:
- sample_weightstr, True, False, oder None, Standardwert=sklearn.utils.metadata_routing.UNCHANGED
Metadaten-Routing für den Parameter
sample_weightinscore.
- Gibt zurück:
- selfobject
Das aktualisierte Objekt.
Galeriebeispiele#
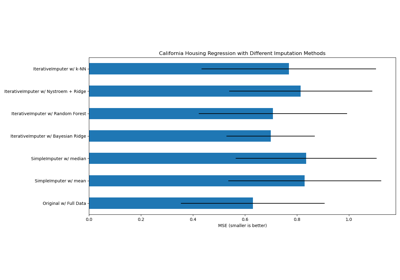
Fehlende Werte mit Varianten von IterativeImputer imputieren

Gesichtsvervollständigung mit Multi-Output-Schätzern