log_loss#
- sklearn.metrics.log_loss(y_true, y_pred, *, normalize=True, sample_weight=None, labels=None)[Quelle]#
Log-Loss, auch bekannt als logistischer Verlust oder Kreuzentropieverlust.
Dies ist die Verlustfunktion, die in der (multinomialen) logistischen Regression und deren Erweiterungen wie neuronalen Netzen verwendet wird. Sie ist definiert als die negative Log-Likelihood eines logistischen Modells, das die Wahrscheinlichkeiten
y_predfür seine Trainingsdateny_truezurückgibt. Der Log-Verlust ist nur für zwei oder mehr Klassen definiert. Für eine einzelne Stichprobe mit der wahren Klasse \(y \in \{0,1\}\) und einer Wahrscheinlichkeitsschätzung \(p = \operatorname{Pr}(y = 1)\) ist der Log-Verlust\[L_{\log}(y, p) = -(y \log (p) + (1 - y) \log (1 - p))\]Lesen Sie mehr im Benutzerhandbuch.
- Parameter:
- y_truearray-ähnlich oder Label-Indikatormatrix
Tatsächliche (korrekte) Labels für n_samples Stichproben.
- y_predarray-ähnlich von float, Form = (n_samples, n_classes) oder (n_samples,)
Vorhergesagte Wahrscheinlichkeiten, wie sie von der predict_proba Methode eines Klassifikators zurückgegeben werden. Wenn
y_pred.shape = (n_samples,), werden die angegebenen Wahrscheinlichkeiten für die positive Klasse angenommen. Die Labels iny_predwerden alphabetisch geordnet angenommen, wie es vonLabelBinarizergehandhabt wird.y_predWerte werden auf[eps, 1-eps]gekappt, wobeiepsdie Maschinengenauigkeit für den Datentyp vony_predist.- normalizebool, default=True
Wenn wahr, wird der mittlere Verlust pro Stichprobe zurückgegeben. Andernfalls wird die Summe der per-Stichproben-Verluste zurückgegeben.
- sample_weightarray-like der Form (n_samples,), Standardwert=None
Stichprobengewichte.
- labelsarray-artig, Standardwert=None
Wenn nicht angegeben, werden die Labels aus y_true abgeleitet. Wenn
labelsNoneist undy_preddie Form (n_samples,) hat, werden die Labels als binär angenommen und ausy_trueabgeleitet.Hinzugefügt in Version 0.18.
- Gibt zurück:
- lossfloat
Log-Loss, auch bekannt als logistischer Verlust oder Kreuzentropieverlust.
Anmerkungen
Der verwendete Logarithmus ist der natürliche Logarithmus (Basis e).
Referenzen
C.M. Bishop (2006). Pattern Recognition and Machine Learning. Springer, S. 209.
Beispiele
>>> from sklearn.metrics import log_loss >>> log_loss(["spam", "ham", "ham", "spam"], ... [[.1, .9], [.9, .1], [.8, .2], [.35, .65]]) 0.21616
Galeriebeispiele#
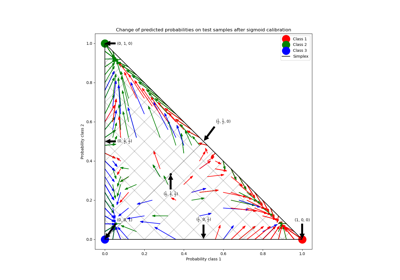
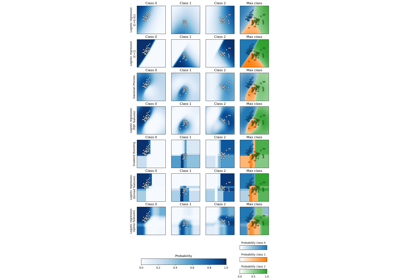
Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation
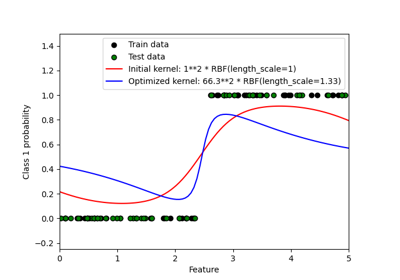
Probabilistische Vorhersagen mit Gauß-Prozess-Klassifikation (GPC)