1.14. Semi-supervised learning#
Semi-supervised learning ist eine Situation, in der in Ihren Trainingsdaten einige der Stichproben nicht gekennzeichnet sind. Die semi-superviseden Estimators in sklearn.semi_supervised können diese zusätzlichen unbeschrifteten Daten nutzen, um die Form der zugrunde liegenden Datenverteilung besser zu erfassen und besser auf neue Stichproben zu generalisieren. Diese Algorithmen können gut funktionieren, wenn wir eine sehr geringe Anzahl beschrifteter Punkte und eine große Anzahl unbeschrifteter Punkte haben.
Hinweis
Semi-supervisede Algorithmen müssen Annahmen über die Verteilung des Datensatzes treffen, um Leistungsgewinne zu erzielen. Weitere Einzelheiten finden Sie hier.
Beispiele
1.14.1. Self Training#
Diese Self-Training-Implementierung basiert auf Yarowskys Algorithmus [1]. Mit diesem Algorithmus kann ein gegebener supervised Klassifikator als semi-supervised Klassifikator fungieren, wodurch er aus unbeschrifteten Daten lernen kann.
SelfTrainingClassifier kann mit jedem Klassifikator aufgerufen werden, der predict_proba implementiert, der als Parameter estimator übergeben wird. In jeder Iteration sagt der estimator Labels für die unbeschrifteten Stichproben voraus und fügt eine Teilmenge dieser Labels zum beschrifteten Datensatz hinzu.
Die Wahl dieser Teilmenge wird durch das Auswahlkriterium bestimmt. Diese Auswahl kann mittels eines threshold auf die Vorhersagewahrscheinlichkeiten erfolgen oder durch Auswahl der k_best Stichproben entsprechend den Vorhersagewahrscheinlichkeiten.
Die für den endgültigen Fit verwendeten Labels sowie die Iteration, in der jede Stichprobe beschriftet wurde, sind als Attribute verfügbar. Der optionale Parameter max_iter gibt an, wie oft die Schleife höchstens ausgeführt wird.
Der Parameter max_iter kann auf None gesetzt werden, wodurch der Algorithmus so lange iteriert, bis alle Stichproben beschriftet sind oder in einer Iteration keine neuen Stichproben ausgewählt werden.
Hinweis
Bei Verwendung des Self-Training-Klassifikators ist die Kalibrierung des Klassifikators wichtig.
Beispiele
Auswirkung der Änderung des Schwellenwerts für Self-Training
Entscheidungsgrenze semi-überwachter Klassifikatoren vs. SVM auf dem Iris-Datensatz
Referenzen
1.14.2. Label Propagation#
Label Propagation bezeichnet einige Varianten von semi-superviseden Graph-Inferenz-Algorithmen.
- Einige verfügbare Funktionen in diesem Modell
Verwendet für Klassifizierungsaufgaben
Kernel-Methoden zur Projektion von Daten in alternative dimensionale Räume
scikit-learn bietet zwei Label Propagation Modelle: LabelPropagation und LabelSpreading. Beide funktionieren durch Konstruktion eines Ähnlichkeitsgraphen über alle Elemente im Eingabedatensatz.
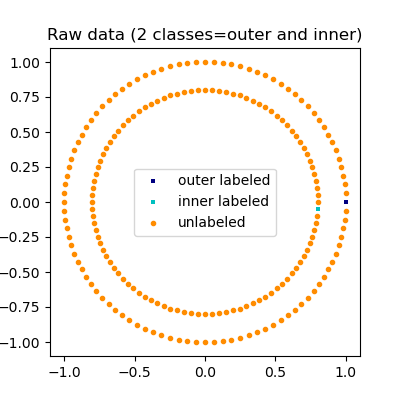
Eine Illustration der Label-Propagation: die Struktur unbeschrifteter Beobachtungen stimmt mit der Klassenstruktur überein, und somit kann die Klassenbezeichnung auf die unbeschrifteten Beobachtungen des Trainingssatzes propagiert werden.#
LabelPropagation und LabelSpreading unterscheiden sich in Modifikationen der Ähnlichkeitsmatrix des Graphen und dem Clamping-Effekt auf die Label-Verteilungen. Clamping ermöglicht es dem Algorithmus, das Gewicht der wahren, beschrifteten Daten bis zu einem gewissen Grad zu ändern. Der Algorithmus LabelPropagation führt ein hartes Clamping von Eingabe-Labels durch, was bedeutet, dass \(\alpha=0\) ist. Dieser Clamping-Faktor kann gelockert werden, z. B. auf \(\alpha=0.2\), was bedeutet, dass wir immer 80 Prozent unserer ursprünglichen Label-Verteilung beibehalten, aber der Algorithmus seine Konfidenz der Verteilung innerhalb von 20 Prozent ändern kann.
LabelPropagation verwendet die rohe Ähnlichkeitsmatrix, die aus den Daten ohne Modifikationen konstruiert wurde. Im Gegensatz dazu minimiert LabelSpreading eine Verlustfunktion, die Regularisierungseigenschaften aufweist, und ist daher oft robuster gegenüber Rauschen. Der Algorithmus iteriert über eine modifizierte Version des ursprünglichen Graphen und normalisiert die Kantengewichte durch Berechnung der normalisierten Graph-Laplace-Matrix. Dieses Verfahren wird auch bei der Spektralen Clusterbildung verwendet.
Label Propagation Modelle haben zwei eingebaute Kernel-Methoden. Die Wahl des Kernels beeinflusst sowohl die Skalierbarkeit als auch die Leistung der Algorithmen. Die folgenden sind verfügbar
rbf (\(\exp(-\gamma |x-y|^2), \gamma > 0\)). \(\gamma\) wird über das Schlüsselwort gamma spezifiziert.
knn (\(1[x' \in kNN(x)]\)). \(k\) wird über das Schlüsselwort n_neighbors spezifiziert.
Der RBF-Kernel erzeugt einen vollvernetzten Graphen, der im Speicher als dichte Matrix dargestellt wird. Diese Matrix kann sehr groß sein und, kombiniert mit den Kosten einer vollständigen Matrixmultiplikationsberechnung für jede Iteration des Algorithmus, zu prohibitiv langen Laufzeiten führen. Auf der anderen Seite erzeugt der KNN-Kernel eine wesentlich speichereffizientere dünne Matrix, die die Laufzeiten drastisch reduzieren kann.
Beispiele
Referenzen
[2] Yoshua Bengio, Olivier Delalleau, Nicolas Le Roux. In Semi-Supervised Learning (2006), S. 193-216
[3] Olivier Delalleau, Yoshua Bengio, Nicolas Le Roux. Efficient Non-Parametric Function Induction in Semi-Supervised Learning. AISTAT 2005 https://www.gatsby.ucl.ac.uk/aistats/fullpapers/204.pdf