1.4. Support Vector Machines#

Support Vector Machines (SVMs) sind eine Sammlung von überwachten Lernmethoden, die für Klassifikation, Regression und Ausreißererfassung verwendet werden.

Die Vorteile von Support Vector Machines sind:

  • Effektiv in hochdimensionalen Räumen.

  • Immer noch effektiv in Fällen, in denen die Anzahl der Dimensionen größer ist als die Anzahl der Stichproben.

  • Verwendet eine Teilmenge der Trainingspunkte in der Entscheidungsfunktion (sogenannte Stützvektoren), was ihn auch speichereffizient macht.

  • Vielseitig: Verschiedene Kernel-Funktionen können für die Entscheidungsfunktion angegeben werden. Gängige Kernel sind vorhanden, aber es ist auch möglich, benutzerdefinierte Kernel anzugeben.

Die Nachteile von Support Vector Machines umfassen:

  • Wenn die Anzahl der Merkmale viel größer ist als die Anzahl der Stichproben, ist es entscheidend, Überanpassung bei der Auswahl von Kernel-Funktionen und Regularisierungstermen zu vermeiden.

  • SVMs liefern keine direkten Wahrscheinlichkeitsschätzungen, diese werden mithilfe einer aufwendigen fünf-fachen Kreuzvalidierung berechnet (siehe Scores und Wahrscheinlichkeiten, unten).

Die Support Vector Machines in scikit-learn unterstützen sowohl dichte (numpy.ndarray und durch numpy.asarray konvertierbar) als auch dünne (beliebige scipy.sparse) Stichprobenvektoren als Eingabe. Um jedoch einen SVM zur Vorhersage für dünne Daten zu verwenden, muss er auf solchen Daten trainiert worden sein. Für optimale Leistung verwenden Sie C-kontinuierliche numpy.ndarray (dicht) oder scipy.sparse.csr_matrix (dünn) mit dtype=float64.

1.4.1. Klassifikation#

SVC, NuSVC und LinearSVC sind Klassen, die binäre und multiklassige Klassifikation auf einem Datensatz durchführen können.

../_images/sphx_glr_plot_iris_svc_001.png

SVC und NuSVC sind ähnliche Methoden, akzeptieren aber leicht unterschiedliche Parametersätze und haben unterschiedliche mathematische Formulierungen (siehe Abschnitt Mathematische Formulierung). LinearSVC hingegen ist eine weitere (schnellere) Implementierung der Support Vector Classification für den Fall eines linearen Kernels. Ihr fehlen auch einige Attribute von SVC und NuSVC, wie support_. LinearSVC verwendet den squared_hinge Verlust und aufgrund seiner Implementierung in liblinear wird auch der Achsenabschnitt (intercept) regularisiert, falls berücksichtigt. Dieser Effekt kann jedoch durch sorgfältige Abstimmung seines intercept_scaling Parameters reduziert werden, der dem Achsenabschnittsparameter ein anderes Regularisierungsverhalten als den übrigen Merkmalen ermöglicht. Die Klassifizierungsergebnisse und der Score können daher von den beiden anderen Klassifikatoren abweichen.

Wie andere Klassifikatoren nehmen SVC, NuSVC und LinearSVC als Eingabe zwei Arrays entgegen: ein Array X der Form (n_samples, n_features) mit den Trainingsstichproben und ein Array y mit den Klassenlabels (Zeichenketten oder ganze Zahlen) der Form (n_samples).

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)
SVC()

Nach dem Trainieren kann das Modell dann zur Vorhersage neuer Werte verwendet werden.

>>> clf.predict([[2., 2.]])
array([1])

Die Entscheidungsfunktion von SVMs (detailliert in Mathematische Formulierung) hängt von einer Teilmenge der Trainingsdaten ab, den sogenannten Stützvektoren. Einige Eigenschaften dieser Stützvektoren finden sich in den Attributen support_vectors_, support_ und n_support_.

>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # get indices of support vectors
>>> clf.support_
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_
array([1, 1]...)

Beispiele

1.4.1.1. Multiklassifizierung#

SVC und NuSVC implementieren den "one-versus-one" ("ovo") Ansatz für die Multiklassifizierung, der n_classes * (n_classes - 1) / 2 Klassifikatoren konstruiert, die jeweils auf Daten aus zwei Klassen trainiert werden. Intern verwendet der Solver immer diese "ovo"-Strategie zum Trainieren der Modelle. Standardmäßig ist der Parameter decision_function_shape jedoch auf "ovr" ("one-vs-rest") gesetzt, um eine konsistente Schnittstelle zu anderen Klassifikatoren zu gewährleisten, indem die "ovo"-Entscheidungsfunktion monoton in eine "ovr"-Entscheidungsfunktion der Form (n_samples, n_classes) umgewandelt wird.

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(decision_function_shape='ovo')
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 6 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

Andererseits implementiert LinearSVC eine "one-vs-rest" ("ovr") Multiklassenstrategie, wodurch n_classes Modelle trainiert werden.

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC()
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

Siehe Mathematische Formulierung für eine vollständige Beschreibung der Entscheidungsfunktion.

Details zu Multiklassenstrategien#

Beachten Sie, dass LinearSVC auch eine alternative Multiklassenstrategie implementiert, die sogenannte multiklassige SVM, die von Crammer und Singer [16] formuliert wurde, durch die Option multi_class='crammer_singer'. In der Praxis wird die "one-vs-rest"-Klassifizierung üblicherweise bevorzugt, da die Ergebnisse meist ähnlich sind, aber die Laufzeit deutlich geringer ist.

Für "one-vs-rest" LinearSVC haben die Attribute coef_ und intercept_ die Form (n_classes, n_features) bzw. (n_classes,). Jede Zeile der Koeffizienten entspricht einem der n_classes "one-vs-rest"-Klassifikatoren und ähnlich für die Achsenabschnitte, in der Reihenfolge der "one"-Klasse.

Im Fall von "one-vs-one" SVC und NuSVC ist das Layout der Attribute etwas komplexer. Bei einem linearen Kernel haben die Attribute coef_ und intercept_ die Form (n_classes * (n_classes - 1) / 2, n_features) und (n_classes * (n_classes - 1) / 2). Dies ähnelt dem Layout für LinearSVC oben beschrieben, wobei jede Zeile nun einem binären Klassifikator entspricht. Die Reihenfolge für die Klassen 0 bis n ist "0 gegen 1", "0 gegen 2", ..., "0 gegen n", "1 gegen 2", "1 gegen 3", "1 gegen n", ..., "n-1 gegen n".

Die Form von dual_coef_ ist (n_classes-1, n_SV) mit einem etwas schwer zu verstehenden Layout. Die Spalten entsprechen den Stützvektoren, die an einem der n_classes * (n_classes - 1) / 2 "one-vs-one"-Klassifikatoren beteiligt sind. Jeder Stützvektor v hat einen dualen Koeffizienten in jedem der n_classes - 1 Klassifikatoren, die die Klasse von v gegen eine andere Klasse vergleichen. Beachten Sie, dass einige, aber nicht alle, dieser dualen Koeffizienten Null sein können. Die n_classes - 1 Einträge in jeder Spalte sind diese dualen Koeffizienten, geordnet nach der gegenübergestellten Klasse.

Dies ist möglicherweise mit einem Beispiel klarer: Betrachten Sie ein Dreiklassenproblem mit Klasse 0, das drei Stützvektoren \(v^{0}_0, v^{1}_0, v^{2}_0\) hat, und Klasse 1 und 2, die jeweils zwei Stützvektoren \(v^{0}_1, v^{1}_1\) und \(v^{0}_2, v^{1}_2\) haben. Für jeden Stützvektor \(v^{j}_i\) gibt es zwei duale Koeffizienten. Nennen wir den Koeffizienten des Stützvektors \(v^{j}_i\) im Klassifikator zwischen den Klassen \(i\) und \(k\) \(\alpha^{j}_{i,k}\). Dann sieht dual_coef_ wie folgt aus:

\(\alpha^{0}_{0,1}\)

\(\alpha^{1}_{0,1}\)

\(\alpha^{2}_{0,1}\)

\(\alpha^{0}_{1,0}\)

\(\alpha^{1}_{1,0}\)

\(\alpha^{0}_{2,0}\)

\(\alpha^{1}_{2,0}\)

\(\alpha^{0}_{0,2}\)

\(\alpha^{1}_{0,2}\)

\(\alpha^{2}_{0,2}\)

\(\alpha^{0}_{1,2}\)

\(\alpha^{1}_{1,2}\)

\(\alpha^{0}_{2,1}\)

\(\alpha^{1}_{2,1}\)

Koeffizienten für SVs der Klasse 0

Koeffizienten für SVs der Klasse 1

Koeffizienten für SVs der Klasse 2

Beispiele

1.4.1.2. Scores und Wahrscheinlichkeiten#

Die Methode decision_function von SVC und NuSVC liefert klassenbezogene Scores für jede Stichprobe (oder einen einzelnen Score pro Stichprobe im binären Fall). Wenn die Konstruktoroption probability auf True gesetzt ist, sind Klassenzugehörigkeitswahrscheinlichkeitsschätzungen (aus den Methoden predict_proba und predict_log_proba) aktiviert. Im binären Fall werden die Wahrscheinlichkeiten mittels Platt-Skalierung [9] kalibriert: logistische Regression auf den SVM-Scores, die durch zusätzliche Kreuzvalidierung auf den Trainingsdaten angepasst wird. Im Multiklassenfall wird dies nach [10] erweitert.

Hinweis

Das gleiche Wahrscheinlichkeitskalibrierungsverfahren ist für alle Schätzer über CalibratedClassifierCV verfügbar (siehe Wahrscheinlichkeitskalibrierung). Im Fall von SVC und NuSVC ist dieses Verfahren in libsvm integriert, das im Hintergrund verwendet wird, sodass es nicht auf scikit-learns CalibratedClassifierCV angewiesen ist.

Die Kreuzvalidierung, die bei der Platt-Skalierung beteiligt ist, ist eine kostspielige Operation für große Datensätze. Darüber hinaus können die Wahrscheinlichkeitsschätzungen inkonsistent mit den Scores sein

  • Der "argmax" der Scores ist möglicherweise nicht der argmax der Wahrscheinlichkeiten.

  • Bei binärer Klassifikation kann eine Stichprobe von predict als zur positiven Klasse gehörend klassifiziert werden, obwohl die Ausgabe von predict_proba kleiner als 0,5 ist; und ähnlich kann sie als negativ klassifiziert werden, obwohl die Ausgabe von predict_proba größer als 0,5 ist.

Platts Methode ist auch dafür bekannt, theoretische Probleme zu haben. Wenn Konfidenzwerte erforderlich sind, diese aber keine Wahrscheinlichkeiten sein müssen, dann ist es ratsam, probability=False zu setzen und decision_function anstelle von predict_proba zu verwenden.

Bitte beachten Sie, dass bei decision_function_shape='ovr' und n_classes > 2, im Gegensatz zu decision_function, die Methode predict standardmäßig keine Bindungsauflösung versucht. Sie können break_ties=True setzen, damit die Ausgabe von predict mit np.argmax(clf.decision_function(...), axis=1) übereinstimmt, andernfalls wird immer die erste Klasse unter den gebundenen Klassen zurückgegeben; beachten Sie jedoch, dass dies mit einem Rechenaufwand verbunden ist. Siehe SVM Tie Breaking Beispiel für ein Beispiel zum Auflösen von Bindungen.

1.4.1.3. Unausgeglichene Probleme#

Bei Problemen, bei denen bestimmten Klassen oder einzelnen Stichproben mehr Bedeutung beigemessen werden soll, können die Parameter class_weight und sample_weight verwendet werden.

SVC (aber nicht NuSVC) implementiert den Parameter class_weight in der Methode fit. Es handelt sich um ein Dictionary der Form {class_label : value}, wobei value eine Gleitkommazahl > 0 ist, die den Parameter C der Klasse class_label auf C * value setzt. Die folgende Abbildung veranschaulicht die Entscheidungsgrenze eines unausgeglichenen Problems, mit und ohne Gewichtungskorrektur.

../_images/sphx_glr_plot_separating_hyperplane_unbalanced_001.png

SVC, NuSVC, SVR, NuSVR, LinearSVC, LinearSVR und OneClassSVM implementieren auch Gewichte für einzelne Stichproben in der Methode fit über den Parameter sample_weight. Ähnlich wie bei class_weight setzt dies den Parameter C für das i-te Beispiel auf C * sample_weight[i], was den Klassifikator dazu ermutigt, diese Stichproben richtig zu klassifizieren. Die folgende Abbildung veranschaulicht die Auswirkung der Stichprobengewichtung auf die Entscheidungsgrenze. Die Größe der Kreise ist proportional zu den Stichprobengewichten.

../_images/sphx_glr_plot_weighted_samples_001.png

Beispiele

1.4.2. Regression#

Die Methode der Support Vector Classification kann erweitert werden, um Regressionsprobleme zu lösen. Diese Methode wird Support Vector Regression genannt.

Das durch die Support Vector Classification (wie oben beschrieben) erzeugte Modell hängt nur von einer Teilmenge der Trainingsdaten ab, da die Kostenfunktion zur Erstellung des Modells keine Trainingspunkte berücksichtigt, die über den Rand hinausgehen. Analog dazu hängt das durch die Support Vector Regression erzeugte Modell nur von einer Teilmenge der Trainingsdaten ab, da die Kostenfunktion Stichproben ignoriert, deren Vorhersage nahe am Zielwert liegt.

Es gibt drei verschiedene Implementierungen der Support Vector Regression: SVR, NuSVR und LinearSVR. LinearSVR bietet eine schnellere Implementierung als SVR, berücksichtigt aber nur den linearen Kernel, während NuSVR eine leicht abweichende Formulierung als SVR und LinearSVR implementiert. Aufgrund seiner Implementierung in liblinear regularisiert LinearSVR auch den Achsenabschnitt, falls berücksichtigt. Dieser Effekt kann jedoch durch sorgfältige Abstimmung seines intercept_scaling Parameters reduziert werden, der dem Achsenabschnittsparameter ein anderes Regularisierungsverhalten als den übrigen Merkmalen ermöglicht. Die Klassifizierungsergebnisse und der Score können daher von den beiden anderen Klassifikatoren abweichen. Siehe Implementierungsdetails für weitere Informationen.

Wie bei den Klassifizierungsklassen nimmt die Methode fit als Argumente Vektoren X und y entgegen, nur dass in diesem Fall y anstelle von ganzen Zahlen Gleitkommazahlen enthalten soll.

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> regr = svm.SVR()
>>> regr.fit(X, y)
SVR()
>>> regr.predict([[1, 1]])
array([1.5])

Beispiele

1.4.3. Dichteschätzung, Neuentdeckungsdetektion#

Die Klasse OneClassSVM implementiert eine One-Class SVM, die zur Ausreißererfassung verwendet wird.

Siehe Neuentdeckungs- und Ausreißererkennung für die Beschreibung und Verwendung von OneClassSVM.

1.4.4. Komplexität#

Support Vector Machines sind leistungsstarke Werkzeuge, aber ihre Rechen- und Speicheranforderungen steigen schnell mit der Anzahl der Trainingsvektoren. Der Kern eines SVM ist ein quadratisches Optimierungsproblem (QP), das Stützvektoren vom Rest der Trainingsdaten trennt. Der von der libsvm-basierten Implementierung verwendete QP-Solver skaliert zwischen \(O(n_{features} \times n_{samples}^2)\) und \(O(n_{features} \times n_{samples}^3)\), abhängig davon, wie effizient der libsvm-Cache in der Praxis genutzt wird (datensatzabhängig). Wenn die Daten sehr dünn sind, sollte \(n_{features}\) durch die durchschnittliche Anzahl von Nicht-Null-Merkmalen in einem Stichprobenvektor ersetzt werden.

Für den linearen Fall ist der von liblinear implementierte Algorithmus in LinearSVC deutlich effizienter als sein libsvm-basiertes SVC-Gegenstück und kann fast linear auf Millionen von Stichproben und/oder Merkmalen skaliert werden.

1.4.5. Tipps zur praktischen Anwendung#

  • Vermeidung von Datenkopien: Für SVC, SVR, NuSVC und NuSVR werden Daten, die nicht C-kontinuierlich und in doppelter Genauigkeit vorliegen und an bestimmte Methoden übergeben werden, kopiert, bevor die zugrunde liegende C-Implementierung aufgerufen wird. Sie können überprüfen, ob ein gegebenes numpy-Array C-kontinuierlich ist, indem Sie sein Attribut flags untersuchen.

    Für LinearSVC (und LogisticRegression) wird jede als numpy-Array übergebene Eingabe kopiert und in die interne dünne Datenrepräsentation von liblinear (Gleitkommazahlen doppelter Genauigkeit und int32-Indizes von Nicht-Null-Komponenten) umgewandelt. Wenn Sie einen skalierbaren linearen Klassifikator ohne Kopieren eines dichten numpy-Arrays mit C-Kontinuität und doppelter Genauigkeit als Eingabe trainieren möchten, empfehlen wir stattdessen die Verwendung der Klasse SGDClassifier. Die Zielfunktion kann so konfiguriert werden, dass sie sich fast genauso verhält wie das LinearSVC-Modell.

  • Kernel-Cache-Größe: Für SVC, SVR, NuSVC und NuSVR hat die Größe des Kernel-Caches einen starken Einfluss auf die Laufzeiten bei größeren Problemen. Wenn Sie genügend RAM zur Verfügung haben, empfiehlt es sich, cache_size auf einen Wert größer als den Standardwert von 200 (MB) zu setzen, z. B. 500 (MB) oder 1000 (MB).

  • Einstellung von C: C ist standardmäßig 1 und eine vernünftige Standardwahl. Wenn Sie viele verrauschte Beobachtungen haben, sollten Sie es verringern: eine Verringerung von C entspricht einer stärkeren Regularisierung.

    LinearSVC und LinearSVR sind weniger empfindlich gegenüber C, wenn dieser groß wird, und die Vorhersageergebnisse verbessern sich nach einem bestimmten Schwellenwert nicht mehr. Gleichzeitig dauern größere C-Werte länger für das Training, manchmal bis zu 10 Mal länger, wie in [11] gezeigt.

  • Support-Vektor-Maschinen-Algorithmen sind nicht skaleninvariant, daher wird dringend empfohlen, Ihre Daten zu skalieren. Skalieren Sie beispielsweise jedes Attribut des Eingabevektors X auf [0,1] oder [-1,+1], oder standardisieren Sie es so, dass es den Mittelwert 0 und die Varianz 1 hat. Beachten Sie, dass die gleiche Skalierung auf den Testvektor angewendet werden muss, um aussagekräftige Ergebnisse zu erzielen. Dies kann einfach mit einer Pipeline erfolgen.

    >>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.svm import SVC

>>> clf = make_pipeline(StandardScaler(), SVC())

    Siehe Abschnitt Datenvorverarbeitung für weitere Details zur Skalierung und Normalisierung.

  • Bezüglich des Parameters shrinking, zitiert aus [12]: Wir haben festgestellt, dass, wenn die Anzahl der Iterationen groß ist, das Schrumpfen die Trainingszeit verkürzen kann. Wenn wir jedoch das Optimierungsproblem locker lösen (z.B. durch Verwendung einer großen Stopp-Toleranz), kann der Code ohne Schrumpfen viel schneller sein

  • Der Parameter nu in NuSVC/OneClassSVM/NuSVR approximiert den Anteil der Trainingsfehler und Support-Vektoren.

  • In SVC, wenn die Daten unausgeglichen sind (z.B. viele positive und wenige negative), setzen Sie class_weight='balanced' und/oder probieren Sie verschiedene Strafterme C aus.

  • Zufälligkeit der zugrunde liegenden Implementierungen: Die zugrunde liegenden Implementierungen von SVC und NuSVC verwenden einen Zufallszahlengenerator nur zum Mischen der Daten für die Wahrscheinlichkeitsschätzung (wenn probability auf True gesetzt ist). Diese Zufälligkeit kann mit dem Parameter random_state gesteuert werden. Wenn probability auf False gesetzt ist, sind diese Schätzer nicht zufällig und random_state hat keinen Einfluss auf die Ergebnisse. Die zugrunde liegende Implementierung von OneClassSVM ähnelt denen von SVC und NuSVC. Da für OneClassSVM keine Wahrscheinlichkeitsschätzung bereitgestellt wird, ist diese nicht zufällig.

    Die zugrunde liegende Implementierung von LinearSVC verwendet einen Zufallszahlengenerator zur Auswahl von Merkmalen bei der Anpassung des Modells mit der dualen Koordinatenabstiegsmethode (d.h. wenn dual auf True gesetzt ist). Daher ist es nicht ungewöhnlich, leicht unterschiedliche Ergebnisse für dieselben Eingabedaten zu erhalten. Versuchen Sie in diesem Fall, einen kleineren tol-Parameter zu verwenden. Diese Zufälligkeit kann auch mit dem Parameter random_state gesteuert werden. Wenn dual auf False gesetzt ist, ist die zugrunde liegende Implementierung von LinearSVC nicht zufällig und random_state hat keinen Einfluss auf die Ergebnisse.

  • Die Verwendung der L1-Penalisierung, wie sie von LinearSVC(penalty='l1', dual=False) bereitgestellt wird, liefert eine dünnbesetzte Lösung, d.h. nur eine Teilmenge der Merkmalsgewichte ist ungleich Null und trägt zur Entscheidungsfunktion bei. Eine Erhöhung von C führt zu einem komplexeren Modell (mehr Merkmale werden ausgewählt). Der C-Wert, der ein "nulltes" Modell (alle Gewichte gleich Null) ergibt, kann mit l1_min_c berechnet werden.

1.4.6. Kernel-Funktionen#

Die Kernel-Funktion kann eine der folgenden sein

  • linear: \(\langle x, x'\rangle\).

  • polynomial: \((\gamma \langle x, x'\rangle + r)^d\), wobei \(d\) durch den Parameter degree, \(r\) durch coef0 spezifiziert wird.

  • rbf: \(\exp(-\gamma \|x-x'\|^2)\), wobei \(\gamma\) durch den Parameter gamma spezifiziert wird, muss größer als 0 sein.

  • sigmoid \(\tanh(\gamma \langle x,x'\rangle + r)\), wobei \(r\) durch coef0 spezifiziert wird.

Unterschiedliche Kerne werden durch den Parameter kernel spezifiziert.

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

Siehe auch Kernel-Approximation für eine Lösung zur Verwendung von RBF-Kernen, die viel schneller und skalierbarer ist.

1.4.6.1. Parameter des RBF-Kerns#

Beim Trainieren eines SVM mit dem Radial Basis Function (RBF)-Kernel müssen zwei Parameter berücksichtigt werden: C und gamma. Der Parameter C, der allen SVM-Kernen gemeinsam ist, tauscht Fehlklassifizierungen von Trainingsbeispielen gegen die Einfachheit der Entscheidungsoberfläche ein. Ein niedriges C macht die Entscheidungsoberfläche glatt, während ein hohes C darauf abzielt, alle Trainingsbeispiele korrekt zu klassifizieren. gamma bestimmt, wie stark ein einzelnes Trainingsbeispiel Einfluss hat. Je größer gamma ist, desto näher müssen andere Beispiele sein, um beeinflusst zu werden.

Die richtige Wahl von C und gamma ist entscheidend für die Leistung des SVM. Es wird empfohlen, GridSearchCV mit C und gamma zu verwenden, die exponentiell weit auseinander liegen, um gute Werte auszuwählen.

Beispiele

1.4.6.2. Benutzerdefinierte Kerne#

Sie können Ihre eigenen Kerne definieren, indem Sie entweder den Kern als Python-Funktion übergeben oder die Gram-Matrix vordefinieren.

Klassifikatoren mit benutzerdefinierten Kernen verhalten sich genauso wie andere Klassifikatoren, mit der Ausnahme, dass

  • Das Feld support_vectors_ ist nun leer, nur die Indizes der Support-Vektoren werden in support_ gespeichert.

  • Eine Referenz (und keine Kopie) des ersten Arguments in der fit()-Methode wird für zukünftige Referenz gespeichert. Wenn sich dieses Array zwischen der Verwendung von fit() und predict() ändert, erhalten Sie unerwartete Ergebnisse.

Verwendung von Python-Funktionen als Kerne#

Sie können Ihre eigenen definierten Kerne verwenden, indem Sie eine Funktion an den Parameter kernel übergeben.

Ihr Kern muss als Argumente zwei Matrizen der Form (n_samples_1, n_features), (n_samples_2, n_features) erhalten und eine Kernmatrix der Form (n_samples_1, n_samples_2) zurückgeben.

Der folgende Code definiert einen linearen Kern und erstellt eine Klassifikator-Instanz, die diesen Kern verwendet.

>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
...     return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)
Verwendung der Gram-Matrix#

Sie können vordefinierte Kerne übergeben, indem Sie die Option kernel='precomputed' verwenden. Sie sollten dann die Gram-Matrix anstelle von X an die Methoden fit und predict übergeben. Die Kernelwerte zwischen allen Trainingsvektoren und den Testvektoren müssen angegeben werden.

>>> import numpy as np
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import svm
>>> X, y = make_classification(n_samples=10, random_state=0)
>>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0)
>>> clf = svm.SVC(kernel='precomputed')
>>> # linear kernel computation
>>> gram_train = np.dot(X_train, X_train.T)
>>> clf.fit(gram_train, y_train)
SVC(kernel='precomputed')
>>> # predict on training examples
>>> gram_test = np.dot(X_test, X_train.T)
>>> clf.predict(gram_test)
array([0, 1, 0])

Beispiele

1.4.7. Mathematische Formulierung#

Eine Support-Vektor-Maschine konstruiert eine Hyperebene oder eine Menge von Hyperebenen in einem hohen oder unendlichen dimensionalen Raum, die für Klassifizierung, Regression oder andere Aufgaben verwendet werden kann. Intuitiv wird eine gute Trennung durch die Hyperebene erreicht, die den größten Abstand zu den nächstgelegenen Trainingsdatenpunkten jeder Klasse hat (sogenannter funktionaler Rand), da im Allgemeinen, je größer der Rand, desto geringer der Generalisierungsfehler des Klassifikators ist. Die folgende Abbildung zeigt die Entscheidungsfunktion für ein linear trennbares Problem mit drei Stichproben an den Randschranken, die als „Support-Vektoren“ bezeichnet werden.

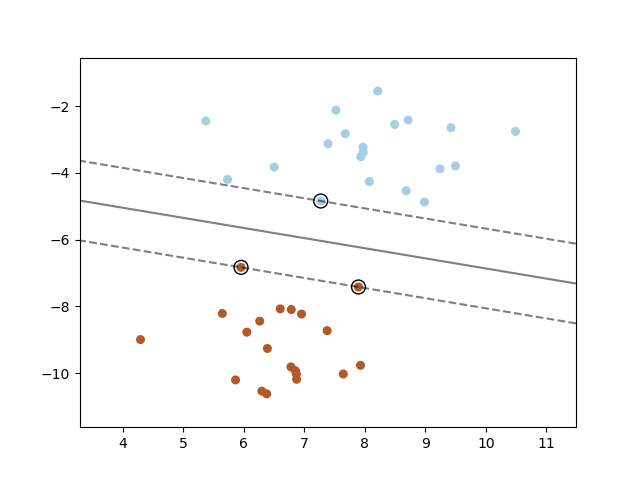
../_images/sphx_glr_plot_separating_hyperplane_001.png

Im Allgemeinen, wenn das Problem nicht linear trennbar ist, sind die Support-Vektoren die Stichproben innerhalb der Randschranken.

Wir empfehlen [13] und [14] als gute Referenzen für die Theorie und praktische Aspekte von SVMs.

1.4.7.1. SVC#

Gegeben seien Trainingsvektoren \(x_i \in \mathbb{R}^p\), i=1,..., n, in zwei Klassen, und ein Vektor \(y \in \{1, -1\}^n\), unser Ziel ist es, \(w \in \mathbb{R}^p\) und \(b \in \mathbb{R}\) zu finden, sodass die Vorhersage gegeben durch \(\text{sign} (w^T\phi(x) + b)\) für die meisten Stichproben korrekt ist.

SVC löst das folgende Primärproblem

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta} \frac{1}{2} w^T w + C \sum_{i=1}^{n} \zeta_i\\\begin{split}\textrm {unter den Bedingungen } & y_i (w^T \phi (x_i) + b) \geq 1 - \zeta_i,\\ & \zeta_i \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

Intuitiv versuchen wir, den Rand zu maximieren (indem wir \(||w||^2 = w^Tw\) minimieren) und gleichzeitig eine Strafe zu verhängen, wenn eine Stichprobe falsch klassifiziert wird oder sich innerhalb der Randgrenze befindet. Idealerweise wäre der Wert \(y_i (w^T \phi (x_i) + b)\) für alle Stichproben \(\geq 1\), was eine perfekte Vorhersage anzeigt. Aber Probleme sind normalerweise nicht immer perfekt durch eine Hyperebene trennbar, daher erlauben wir einigen Stichproben, sich in einem Abstand \(\zeta_i\) von ihrer korrekten Randgrenze zu befinden. Der Strafterm C steuert die Stärke dieser Strafe und wirkt daher als inverser Regularisierungsparameter (siehe Notiz unten).

Das duale Problem zum Primärproblem ist

\[ \begin{align}\begin{aligned}\min_{\alpha} \frac{1}{2} \alpha^T Q \alpha - e^T \alpha\\\begin{split} \textrm {unter den Bedingungen } & y^T \alpha = 0\\ & 0 \leq \alpha_i \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

wobei \(e\) der Vektor aller Einsen ist und \(Q\) eine \(n \times n\) positiv semidefinitive Matrix ist, \(Q_{ij} \equiv y_i y_j K(x_i, x_j)\), wobei \(K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) der Kern ist. Die Terme \(\alpha_i\) werden als duale Koeffizienten bezeichnet und sind durch \(C\) nach oben begrenzt. Diese duale Darstellung hebt die Tatsache hervor, dass Trainingsvektoren durch die Funktion \(\phi\) implizit in einen höheren (möglicherweise unendlichen) dimensionalen Raum abgebildet werden: siehe Kernel-Trick.

Nachdem das Optimierungsproblem gelöst ist, wird die Ausgabe von decision_function für eine gegebene Stichprobe \(x\)

\[\sum_{i\in SV} y_i \alpha_i K(x_i, x) + b,\]

und die vorhergesagte Klasse entspricht ihrem Vorzeichen. Wir müssen nur über die Support-Vektoren (d.h. die Stichproben, die innerhalb des Randes liegen) summieren, da die dualen Koeffizienten \(\alpha_i\) für die anderen Stichproben Null sind.

Diese Parameter sind über die Attribute dual_coef_, das das Produkt \(y_i \alpha_i\) enthält, support_vectors_, das die Support-Vektoren enthält, und intercept_, das den unabhängigen Term \(b\) enthält, zugänglich.

Hinweis

Während SVM-Modelle, die von libsvm und liblinear abgeleitet sind, C als Regularisierungsparameter verwenden, verwenden die meisten anderen Schätzer alpha. Die genaue Äquivalenz zwischen dem Regularisierungsbetrag zweier Modelle hängt von der exakten Zielfunktion ab, die vom Modell optimiert wird. Wenn beispielsweise der verwendete Schätzer eine Ridge-Regression ist, ist die Beziehung zwischen ihnen gegeben durch \(C = \frac{1}{\alpha}\).

LinearSVC#

Das Primärproblem kann äquivalent formuliert werden als

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}^{n}\max(0, 1 - y_i (w^T \phi(x_i) + b)),\]

wobei wir den Hinge-Loss verwenden. Dies ist die Form, die direkt von LinearSVC optimiert wird, aber im Gegensatz zur dualen Form beinhaltet diese keine inneren Produkte zwischen Stichproben, sodass der berühmte Kernel-Trick nicht angewendet werden kann. Deshalb unterstützt nur der lineare Kern LinearSVC (\(\phi\) ist die Identitätsfunktion).

NuSVC#

Die \(\nu\)-SVC-Formulierung [15] ist eine Neuparametrisierung der \(C\)-SVC und daher mathematisch äquivalent.

Wir führen einen neuen Parameter \(\nu\) (anstelle von \(C\)) ein, der die Anzahl der Support-Vektoren und Randfehler steuert: \(\nu \in (0, 1]\) ist eine Obergrenze für den Anteil der Randfehler und eine Untergrenze für den Anteil der Support-Vektoren. Ein Randfehler entspricht einer Stichprobe, die sich auf der falschen Seite ihrer Randschranke befindet: sie ist entweder falsch klassifiziert oder sie ist korrekt klassifiziert, liegt aber nicht jenseits des Randes.

1.4.7.2. SVR#

Gegeben seien Trainingsvektoren \(x_i \in \mathbb{R}^p\), i=1,..., n, und ein Vektor \(y \in \mathbb{R}^n\), \(\varepsilon\)-SVR löst das folgende Primärproblem

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta, \zeta^*} \frac{1}{2} w^T w + C \sum_{i=1}^{n} (\zeta_i + \zeta_i^*)\\\begin{split}\textrm {unter den Bedingungen } & y_i - w^T \phi (x_i) - b \leq \varepsilon + \zeta_i,\\ & w^T \phi (x_i) + b - y_i \leq \varepsilon + \zeta_i^*,\\ & \zeta_i, \zeta_i^* \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

Hier bestrafen wir Stichproben, deren Vorhersage mindestens \(\varepsilon\) von ihrem wahren Zielwert abweicht. Diese Stichproben bestrafen das Ziel um \(\zeta_i\) oder \(\zeta_i^*\), je nachdem, ob ihre Vorhersagen über oder unter dem \(\varepsilon\)-Tube liegen.

Das duale Problem ist

\[ \begin{align}\begin{aligned}\min_{\alpha, \alpha^*} \frac{1}{2} (\alpha - \alpha^*)^T Q (\alpha - \alpha^*) + \varepsilon e^T (\alpha + \alpha^*) - y^T (\alpha - \alpha^*)\\\begin{split} \textrm {unter den Bedingungen } & e^T (\alpha - \alpha^*) = 0\\ & 0 \leq \alpha_i, \alpha_i^* \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

wobei \(e\) der Vektor aller Einsen ist, \(Q\) eine \(n \times n\) positiv semidefinitive Matrix ist, \(Q_{ij} \equiv K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) der Kern ist. Hier werden Trainingsvektoren durch die Funktion \(\phi\) implizit in einen höheren (möglicherweise unendlichen) dimensionalen Raum abgebildet.

Die Vorhersage ist

\[\sum_{i \in SV}(\alpha_i - \alpha_i^*) K(x_i, x) + b\]

Diese Parameter sind über die Attribute dual_coef_, das die Differenz \(\alpha_i - \alpha_i^*\) enthält, support_vectors_, das die Support-Vektoren enthält, und intercept_, das den unabhängigen Term \(b\) enthält, zugänglich.

LinearSVR#

Das Primärproblem kann äquivalent formuliert werden als

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}^{n}\max(0, |y_i - (w^T \phi(x_i) + b)| - \varepsilon),\]

wobei wir den Epsilon-insensitiven Verlust verwenden, d.h. Fehler von weniger als \(\varepsilon\) werden ignoriert. Dies ist die Form, die direkt von LinearSVR optimiert wird.

1.4.8. Implementierungsdetails#

Intern verwenden wir libsvm [12] und liblinear [11] für alle Berechnungen. Diese Bibliotheken sind über C und Cython eingebunden. Eine Beschreibung der Implementierung und Details der verwendeten Algorithmen finden Sie in den entsprechenden Veröffentlichungen.

Referenzen