7.7. Kernel Approximation

Dieses Untermodul enthält Funktionen, die die Feature-Abbildungen approximieren, welche bestimmten Kernels entsprechen, wie sie zum Beispiel in Support Vector Machines verwendet werden (siehe Support Vector Machines). Die folgenden Feature-Funktionen führen nichtlineare Transformationen der Eingabe durch, die als Grundlage für lineare Klassifizierung oder andere Algorithmen dienen können.

Der Vorteil der Verwendung von approximierten expliziten Feature-Maps im Vergleich zum Kernel-Trick, der Feature-Maps implizit nutzt, besteht darin, dass explizite Abbildungen besser für Online-Lernen geeignet sind und die Kosten für das Lernen mit sehr großen Datensätzen erheblich reduzieren können. Standard-Kernel-SVMs skalieren nicht gut für große Datensätze, aber durch die Verwendung einer approximierten Kernel-Map ist es möglich, viel effizientere lineare SVMs zu verwenden. Insbesondere kann die Kombination von Kernel-Map-Approximationen mit SGDClassifier nichtlineares Lernen auf großen Datensätzen ermöglichen.

Da es noch nicht viel empirische Arbeit mit approximierten Embeddings gibt, ist es ratsam, die Ergebnisse nach Möglichkeit mit exakten Kernel-Methoden zu vergleichen.

Siehe auch

Polynomielle Regression: Erweiterung linearer Modelle mit Basisfunktionen für eine exakte polynomielle Transformation.

7.7.1. Nystroem-Methode zur Kernel-Approximation

Die Nystroem-Methode, wie sie in Nystroem implementiert ist, ist eine allgemeine Methode zur Rangreduktion von Kernels. Sie erreicht dies durch Subsampling ohne Zurücklegen von Zeilen/Spalten der Daten, auf denen der Kernel ausgewertet wird. Während die rechnerische Komplexität der exakten Methode \(\mathcal{O}(n^3_{\text{samples}})\) beträgt, beträgt die Komplexität der Approximation \(\mathcal{O}(n^2_{\text{components}} \cdot n_{\text{samples}})\), wobei \(n_{\text{components}} \ll n_{\text{samples}}\) ohne signifikanten Leistungsabfall gesetzt werden kann [WS2001].

Wir können die Eigenzerlegung der Kernel-Matrix \(K\) basierend auf den Merkmalen der Daten konstruieren und diese dann in gestichprobt und nicht gestichprobt Datenpunkte aufteilen.

\[\begin{split}K = U \Lambda U^T = \begin{bmatrix} U_1 \\ U_2\end{bmatrix} \Lambda \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}^T = \begin{bmatrix} U_1 \Lambda U_1^T & U_1 \Lambda U_2^T \\ U_2 \Lambda U_1^T & U_2 \Lambda U_2^T \end{bmatrix} \equiv \begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix}\end{split}\]

wobei

• \(U\) ist orthonormal

• \(\Lambda\) ist eine Diagonalmatrix von Eigenwerten

• \(U_1\) ist die orthogonale Matrix der ausgewählten Stichproben

• \(U_2\) ist die orthogonale Matrix der nicht ausgewählten Stichproben

Da \(U_1 \Lambda U_1^T\) durch Orthonormalisierung der Matrix \(K_{11}\) erhalten werden kann und \(U_2 \Lambda U_1^T\) (sowie seine Transponierte) ausgewertet werden kann, bleibt nur noch der Term \(U_2 \Lambda U_2^T\) zu klären. Dazu können wir ihn in Bezug auf die bereits ausgewerteten Matrizen ausdrücken

\[\begin{split}\begin{align} U_2 \Lambda U_2^T &= \left(K_{21} U_1 \Lambda^{-1}\right) \Lambda \left(K_{21} U_1 \Lambda^{-1}\right)^T \\&= K_{21} U_1 (\Lambda^{-1} \Lambda) \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} U_1 \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} K_{11}^{-1} K_{21}^T \\&= \left( K_{21} K_{11}^{-\frac12} \right) \left( K_{21} K_{11}^{-\frac12} \right)^T .\end{align}\end{split}\]

Während des fit-Vorgangs wertet die Klasse Nystroem die Basis \(U_1\) aus und berechnet die Normalisierungskonstante \(K_{11}^{-\frac12}\). Später, während des transform-Vorgangs, wird die Kernel-Matrix zwischen der Basis (gegeben durch das Attribut components_) und den neuen Datenpunkten, X, ausgewertet. Diese Matrix wird dann mit der normalization_-Matrix multipliziert, um das Endergebnis zu erhalten.

Standardmäßig verwendet Nystroem den rbf-Kernel, kann aber jede Kernel-Funktion oder eine vortrainierte Kernel-Matrix verwenden. Die Anzahl der verwendeten Stichproben – die auch die Dimensionalität der berechneten Features darstellt – wird durch den Parameter n_components bestimmt.

Beispiele

• Siehe das Beispiel mit dem Titel Zeitbezogenes Feature Engineering, das eine effiziente Machine-Learning-Pipeline mit einem Nystroem-Kernel zeigt.

• Siehe Approximation expliziter Feature-Maps für RBF-Kernel für einen Vergleich des Nystroem-Kernels mit RBFSampler.

7.7.2. Radial Basis Function Kernel

Der RBFSampler konstruiert eine approximierte Abbildung für den Radial Basis Function Kernel, auch bekannt als Random Kitchen Sinks [RR2007]. Diese Transformation kann verwendet werden, um eine Kernel-Abbildung explizit zu modellieren, bevor ein linearer Algorithmus, z. B. eine lineare SVM, angewendet wird.

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

Die Abbildung basiert auf einer Monte-Carlo-Approximation der Kernel-Werte. Die fit-Funktion führt das Monte-Carlo-Sampling durch, während die transform-Methode die Abbildung der Daten durchführt. Aufgrund der inhärenten Zufälligkeit des Prozesses können die Ergebnisse zwischen verschiedenen Aufrufen der fit-Funktion variieren.

Die fit-Funktion nimmt zwei Argumente entgegen: n_components, die Ziel-Dimensionalität der Feature-Transformation, und gamma, den Parameter des RBF-Kernels. Ein höheres n_components führt zu einer besseren Approximation des Kernels und liefert Ergebnisse, die den von einer Kernel-SVM produzierten ähnlicher sind. Beachten Sie, dass das "Fitting" der Feature-Funktion nicht tatsächlich von den Daten abhängt, die der fit-Funktion übergeben werden. Nur die Dimensionalität der Daten wird verwendet. Details zur Methode finden Sie in [RR2007].

Bei einem gegebenen Wert von n_components ist RBFSampler oft weniger genau als Nystroem. RBFSampler ist jedoch kostengünstiger zu berechnen, was die Verwendung größerer Feature-Räume effizienter macht.

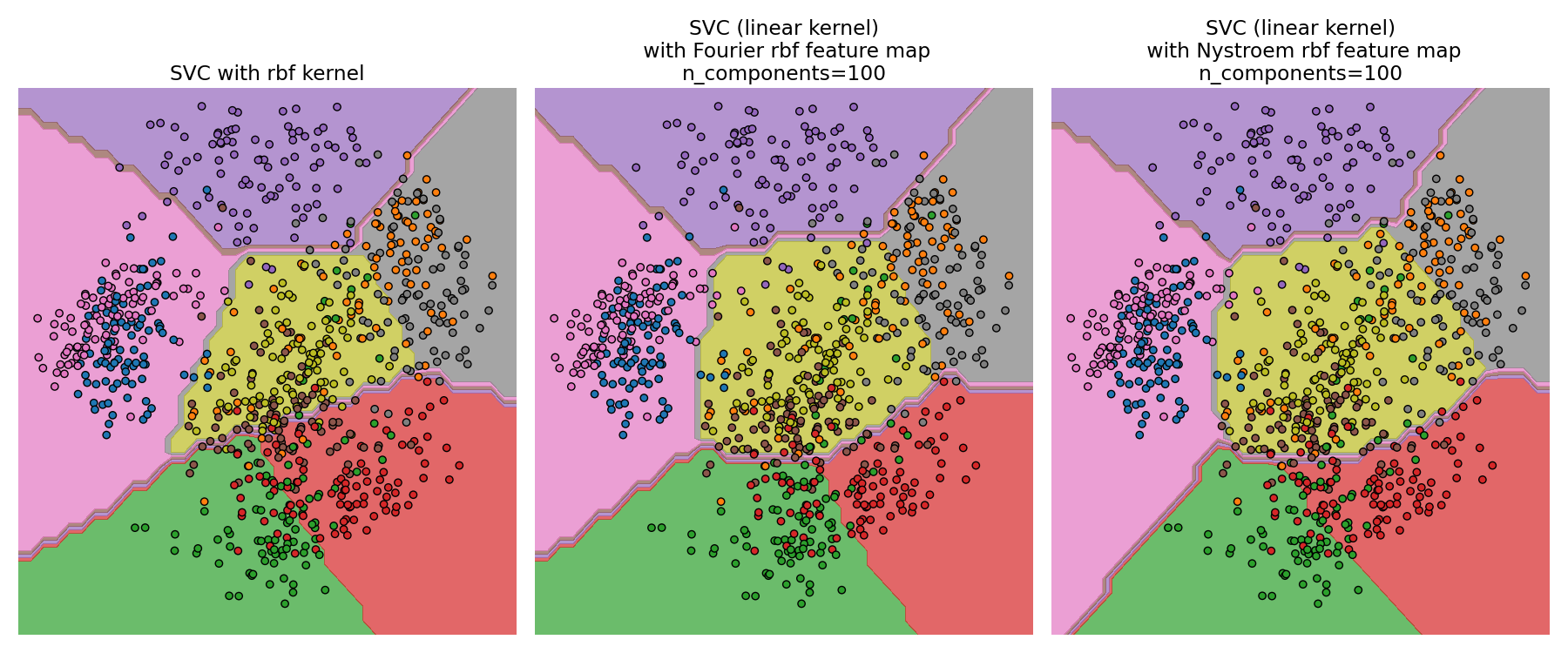
Vergleich eines exakten RBF-Kernels (links) mit der Approximation (rechts)

Beispiele

• Siehe Approximation expliziter Feature-Maps für RBF-Kernel für einen Vergleich des Nystroem-Kernels mit RBFSampler.

7.7.3. Additiver Chi-Quadrat-Kernel

Der additive Chi-Quadrat-Kernel ist ein Kernel für Histogramme, der häufig in der Computer Vision verwendet wird.

Der hier verwendete additive Chi-Quadrat-Kernel ist gegeben durch

\[k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}\]

Dies ist nicht exakt dasselbe wie sklearn.metrics.pairwise.additive_chi2_kernel. Die Autoren von [VZ2010] bevorzugen die obige Version, da sie immer positiv definit ist. Da der Kernel additiv ist, ist es möglich, alle Komponenten \(x_i\) separat für die Einbettung zu behandeln. Dies ermöglicht das Abtasten der Fourier-Transformation in regelmäßigen Intervallen anstelle der Approximation mittels Monte-Carlo-Sampling.

Die Klasse AdditiveChi2Sampler implementiert dieses komponentenweise deterministische Sampling. Jede Komponente wird \(n\) Mal abgetastet, was zu \(2n+1\) Dimensionen pro Eingabedimension führt (der Faktor zwei ergibt sich aus dem realen und imaginären Teil der Fourier-Transformation). In der Literatur wird \(n\) üblicherweise auf 1 oder 2 gesetzt, wodurch der Datensatz auf die Größe n_samples * 5 * n_features transformiert wird (im Fall von \(n=2\)).

Die von AdditiveChi2Sampler bereitgestellte approximierte Feature-Map kann mit der von RBFSampler bereitgestellten approximierten Feature-Map kombiniert werden, um eine approximierte Feature-Map für den exponentierten Chi-Quadrat-Kernel zu erhalten. Details hierzu finden Sie in [VZ2010] und zur Kombination mit RBFSampler in [VVZ2010].

7.7.4. Schiefer Chi-Quadrat-Kernel

Der schiefe Chi-Quadrat-Kernel ist gegeben durch

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

Er hat Eigenschaften, die dem exponentierten Chi-Quadrat-Kernel, der häufig in der Computer Vision verwendet wird, ähneln, ermöglicht aber eine einfache Monte-Carlo-Approximation der Feature-Map.

Die Verwendung von SkewedChi2Sampler ist dieselbe wie die oben für RBFSampler beschriebene Verwendung. Der einzige Unterschied liegt im freien Parameter, der \(c\) genannt wird. Eine Begründung für diese Abbildung und die mathematischen Details finden Sie in [LS2010].

7.7.5. Approximation des Polynom-Kernels mittels Tensor Sketch

Der Polynom-Kernel ist eine beliebte Art von Kernel-Funktion, gegeben durch

\[k(x, y) = (\gamma x^\top y +c_0)^d\]

wobei

• x, y sind die Eingabevektoren

• d ist der Grad des Kernels

Intuitiv besteht der Feature-Raum des Polynom-Kernels vom Grad d aus allen möglichen Produkten vom Grad d zwischen den Eingabe-Features, was es Lernalgorithmen, die diesen Kernel verwenden, ermöglicht, Wechselwirkungen zwischen Features zu berücksichtigen.

Die TensorSketch [PP2013]-Methode, wie sie in PolynomialCountSketch implementiert ist, ist eine skalierbare, datenunabhängige Methode zur Approximation von Polynom-Kernels. Sie basiert auf dem Konzept des Count Sketch [WIKICS] [CCF2002], einer Dimensionsreduktionstechnik, die der Feature-Hashing-Technik ähnelt, jedoch stattdessen mehrere unabhängige Hash-Funktionen verwendet. TensorSketch erhält einen Count Sketch des äußeren Produkts zweier Vektoren (oder eines Vektors mit sich selbst), der als Approximation des Polynom-Kernel-Feature-Raums dienen kann. Insbesondere berechnet TensorSketch anstatt das äußere Produkt explizit zu berechnen, den Count Sketch der Vektoren und verwendet dann Polynom-Multiplikation über die Fast Fourier Transform, um den Count Sketch ihres äußeren Produkts zu berechnen.

Praktischerweise besteht die Trainingsphase von TensorSketch lediglich darin, einige Zufallsvariablen zu initialisieren. Sie ist daher unabhängig von den Eingabedaten, d.h. sie hängt nur von der Anzahl der Eingabe-Features ab, aber nicht von den Datenwerten. Darüber hinaus kann diese Methode Stichproben in \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\) Zeit transformieren, wobei \(n_{\text{components}}\) die gewünschte Ausgabedimension ist, die durch n_components bestimmt wird.

Beispiele

• Skalierbares Lernen mit Polynom-Kernel-Approximation

7.7.6. Mathematische Details

Kernel-Methoden wie Support Vector Machines oder kernelisierte PCA basieren auf einer Eigenschaft von Reproducing Kernel Hilbert Spaces. Für jede positiv definite Kernel-Funktion \(k\) (ein sogenannter Mercer-Kernel) ist garantiert, dass eine Abbildung \(\phi\) in einen Hilbert-Raum \(\mathcal{H}\) existiert, so dass

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

wobei \(\langle \cdot, \cdot \rangle\) das Skalarprodukt im Hilbert-Raum bezeichnet.

Wenn ein Algorithmus, wie eine lineare Support Vector Machine oder PCA, nur vom Skalarprodukt der Datenpunkte \(x_i\) abhängt, kann der Wert von \(k(x_i, x_j)\) verwendet werden, was der Anwendung des Algorithmus auf die abgebildeten Datenpunkte \(\phi(x_i)\) entspricht. Der Vorteil der Verwendung von \(k\) besteht darin, dass die Abbildung \(\phi\) nie explizit berechnet werden muss, was beliebig große Features (sogar unendlich große) ermöglicht.

Ein Nachteil von Kernel-Methoden ist, dass es bei der Optimierung notwendig sein kann, viele Kernel-Werte \(k(x_i, x_j)\) zu speichern. Wenn ein kernelisierter Klassifikator auf neue Daten \(y_j\) angewendet wird, muss \(k(x_i, y_j)\) berechnet werden, um Vorhersagen zu treffen, möglicherweise für viele verschiedene \(x_i\) aus dem Trainingsdatensatz.

Die Klassen in diesem Untermodul ermöglichen die Approximation der Einbettung \(\phi\), wodurch explizit mit den Darstellungen \(\phi(x_i)\) gearbeitet wird, was die Notwendigkeit der Anwendung des Kernels oder der Speicherung von Trainingsbeispielen überflüssig macht.

Referenzen

[WS2001]

“Using the Nyström method to speed up kernel machines” Williams, C.K.I.; Seeger, M. - 2001.

[RR2007] (1,2)

“Random features for large-scale kernel machines” Rahimi, A. und Recht, B. - Advances in neural information processing 2007,

[LS2010]

“Random Fourier approximations for skewed multiplicative histogram kernels” Li, F., Ionescu, C. und Sminchisescu, C. - Pattern Recognition, DAGM 2010, Lecture Notes in Computer Science.

[VZ2010] (1,2)

“Efficient additive kernels via explicit feature maps” Vedaldi, A. und Zisserman, A. - Computer Vision and Pattern Recognition 2010

[VVZ2010]

“Generalized RBF feature maps for Efficient Detection” Vempati, S. und Vedaldi, A. und Zisserman, A. und Jawahar, CV - 2010

[PP2013]

“Fast and scalable polynomial kernels via explicit feature maps” Pham, N. & Pagh, R. - 2013

[CCF2002]

“Finding frequent items in data streams” Charikar, M., Chen, K. & Farach-Colton - 2002

[WIKICS]

„Wikipedia: Count sketch“