Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel in Ihrem Browser über JupyterLite oder Binder auszuführen.
Zeitbezogenes Feature Engineering#
Dieses Notebook stellt verschiedene Strategien vor, um zeitbezogene Merkmale für eine Fahrradverleih-Nachfrage-Regressionsaufgabe zu nutzen, die stark von Geschäftszyklen (Tage, Wochen, Monate) und jährlichen Saisonzyklen abhängt.
Dabei führen wir ein periodisches Feature Engineering mit der Klasse sklearn.preprocessing.SplineTransformer und ihrer Option extrapolation="periodic" ein.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Datenexploration des Bike Sharing Demand Datensatzes#
Wir beginnen mit dem Laden der Daten aus dem OpenML-Repository.
from sklearn.datasets import fetch_openml
bike_sharing = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
df = bike_sharing.frame
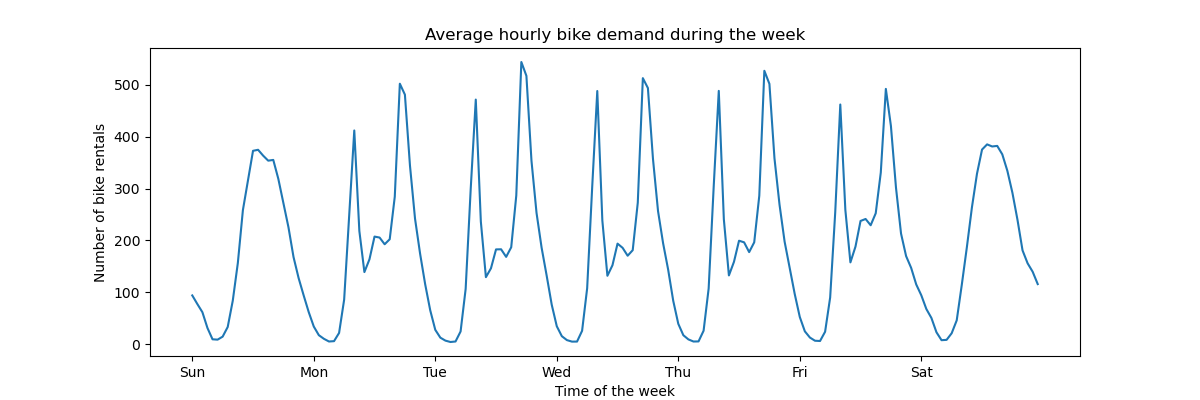
Um ein schnelles Verständnis der periodischen Muster der Daten zu bekommen, betrachten wir die durchschnittliche Nachfrage pro Stunde während einer Woche.
Beachten Sie, dass die Woche am Sonntag beginnt, am Wochenende. Wir können die Pendelmuster am Morgen und Abend der Arbeitstage sowie die Freizeitnutzung der Fahrräder am Wochenende mit einer breiteren Spitzenverfügbarkeit um die Tagesmitte klar unterscheiden.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="Average hourly bike demand during the week",
xticks=[i * 24 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week",
ylabel="Number of bike rentals",
)
Das Ziel des Vorhersageproblems ist die absolute Anzahl der stündlichen Fahrradverleihungen.
df["count"].max()
np.int64(977)
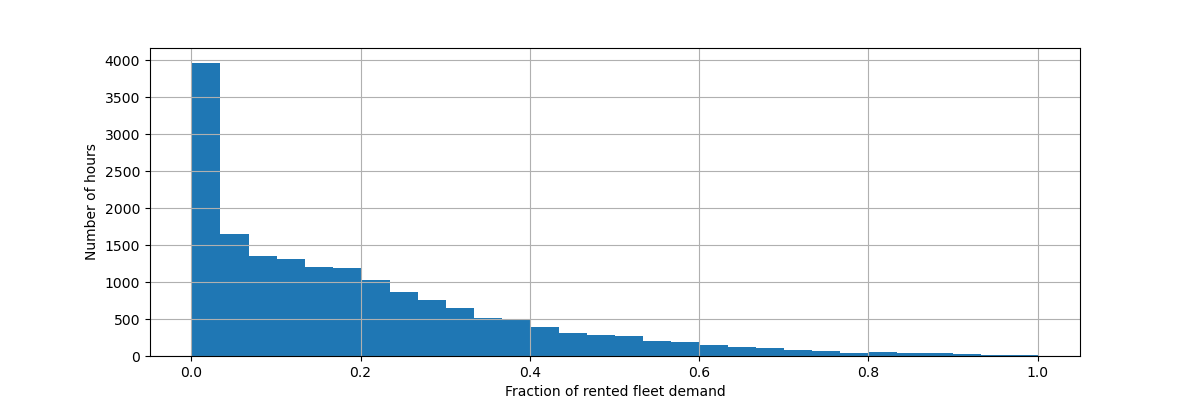
Wir skalieren die Zielvariable (Anzahl der stündlichen Fahrradverleihungen) neu, um eine relative Nachfrage vorherzusagen, so dass der mittlere absolute Fehler leichter als Bruchteil der maximalen Nachfrage interpretiert werden kann.
Hinweis
Die `fit`-Methode der in diesem Notebook verwendeten Modelle minimiert alle den mittleren quadratischen Fehler zur Schätzung des bedingten Mittelwerts. Der absolute Fehler würde jedoch den bedingten Median schätzen.
Nichtsdestotrotz konzentrieren wir uns bei der Berichterstattung von Leistungsmaßen auf dem Testdatensatz in der Diskussion auf den mittleren absoluten Fehler anstelle des (Wurzel-) mittleren quadratischen Fehlers, da dieser intuitiver zu interpretieren ist. Beachten Sie jedoch, dass in dieser Studie die besten Modelle für die eine Metrik auch die besten Modelle in Bezug auf die andere Metrik sind.
y = df["count"] / df["count"].max()
fig, ax = plt.subplots(figsize=(12, 4))
y.hist(bins=30, ax=ax)
_ = ax.set(
xlabel="Fraction of rented fleet demand",
ylabel="Number of hours",
)
Der Eingabemerkmal-Datenrahmen ist ein zeitgestempeltes stündliches Protokoll von Variablen, die die Wetterbedingungen beschreiben. Er enthält sowohl numerische als auch kategoriale Variablen. Beachten Sie, dass die Zeitinformationen bereits in mehrere ergänzende Spalten erweitert wurden.
X = df.drop("count", axis="columns")
X
| saison | jahr | monat | stunde | feiertag | wochentag | arbeitstag | wetter | temp | gefuehlte_temp | feuchtigkeit | windgeschwindigkeit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | fruehling | 0 | 1 | 0 | False | 6 | False | klar | 9.84 | 14.395 | 0.81 | 0.0000 |
| 1 | fruehling | 0 | 1 | 1 | False | 6 | False | klar | 9.02 | 13.635 | 0.80 | 0.0000 |
| 2 | fruehling | 0 | 1 | 2 | False | 6 | False | klar | 9.02 | 13.635 | 0.80 | 0.0000 |
| 3 | fruehling | 0 | 1 | 3 | False | 6 | False | klar | 9.84 | 14.395 | 0.75 | 0.0000 |
| 4 | fruehling | 0 | 1 | 4 | False | 6 | False | klar | 9.84 | 14.395 | 0.75 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | fruehling | 1 | 12 | 19 | False | 1 | True | neblig | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | fruehling | 1 | 12 | 20 | False | 1 | True | neblig | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | fruehling | 1 | 12 | 21 | False | 1 | True | klar | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | fruehling | 1 | 12 | 22 | False | 1 | True | klar | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | fruehling | 1 | 12 | 23 | False | 1 | True | klar | 10.66 | 13.635 | 0.65 | 8.9981 |
17379 Zeilen × 12 Spalten
Hinweis
Wenn die Zeitinformationen nur als Datums- oder `datetime`-Spalte vorhanden wären, hätten wir sie mit Pandas in Stunde-des-Tages, Tag-der-Woche, Tag-des-Monats, Monat-des-Jahres erweitern können: https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#time-date-components
Nun untersuchen wir die Verteilung der kategorialen Variablen, beginnend mit "wetter"
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1419
heavy_rain 3
Name: count, dtype: int64
Da es nur 3 "starker_regen"-Ereignisse gibt, können wir diese Kategorie nicht zum Trainieren von Machine-Learning-Modellen mit Kreuzvalidierung verwenden. Stattdessen vereinfachen wir die Darstellung, indem wir diese mit der Kategorie "regen" zusammenfassen.
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1422
Name: count, dtype: int64
Wie erwartet, ist die Variable "saison" gut ausbalanciert
X["season"].value_counts()
season
fall 4496
summer 4409
spring 4242
winter 4232
Name: count, dtype: int64
Zeitbasierte Kreuzvalidierung#
Da der Datensatz ein zeitlich geordnetes Ereignisprotokoll (stündliche Nachfrage) ist, werden wir einen zeitsensiblen Kreuzvalidierungs-Splitter verwenden, um unser Nachfrageprognosemodell so realistisch wie möglich zu bewerten. Wir verwenden eine Lücke von 2 Tagen zwischen Trainings- und Testseite der Splits. Wir begrenzen auch die Größe des Trainingsdatensatzes, um die Leistung der CV-Folds stabiler zu machen.
1000 Testdatenpunkte sollten ausreichen, um die Leistung des Modells zu quantifizieren. Dies entspricht etwas weniger als eineinhalb Monaten zusammenhängender Testdaten.
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=5,
gap=48,
max_train_size=10000,
test_size=1000,
)
Lassen Sie uns die verschiedenen Splits manuell inspizieren, um zu überprüfen, ob TimeSeriesSplit wie erwartet funktioniert, beginnend mit dem ersten Split
all_splits = list(ts_cv.split(X, y))
train_0, test_0 = all_splits[0]
X.iloc[test_0]
| saison | jahr | monat | stunde | feiertag | wochentag | arbeitstag | wetter | temp | gefuehlte_temp | feuchtigkeit | windgeschwindigkeit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12379 | sommer | 1 | 6 | 0 | False | 2 | True | klar | 22.14 | 25.760 | 0.68 | 27.9993 |
| 12380 | sommer | 1 | 6 | 1 | False | 2 | True | neblig | 21.32 | 25.000 | 0.77 | 22.0028 |
| 12381 | sommer | 1 | 6 | 2 | False | 2 | True | regen | 21.32 | 25.000 | 0.72 | 19.9995 |
| 12382 | sommer | 1 | 6 | 3 | False | 2 | True | regen | 20.50 | 24.240 | 0.82 | 12.9980 |
| 12383 | sommer | 1 | 6 | 4 | False | 2 | True | regen | 20.50 | 24.240 | 0.82 | 12.9980 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 13374 | herbst | 1 | 7 | 11 | False | 1 | True | klar | 34.44 | 40.150 | 0.53 | 15.0013 |
| 13375 | herbst | 1 | 7 | 12 | False | 1 | True | klar | 34.44 | 39.395 | 0.49 | 8.9981 |
| 13376 | herbst | 1 | 7 | 13 | False | 1 | True | klar | 34.44 | 39.395 | 0.49 | 19.0012 |
| 13377 | herbst | 1 | 7 | 14 | False | 1 | True | klar | 36.08 | 40.910 | 0.42 | 7.0015 |
| 13378 | herbst | 1 | 7 | 15 | False | 1 | True | klar | 35.26 | 40.150 | 0.47 | 16.9979 |
1000 Zeilen × 12 Spalten
X.iloc[train_0]
| saison | jahr | monat | stunde | feiertag | wochentag | arbeitstag | wetter | temp | gefuehlte_temp | feuchtigkeit | windgeschwindigkeit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2331 | sommer | 0 | 4 | 1 | False | 2 | True | neblig | 25.42 | 31.060 | 0.50 | 6.0032 |
| 2332 | sommer | 0 | 4 | 2 | False | 2 | True | neblig | 24.60 | 31.060 | 0.53 | 8.9981 |
| 2333 | sommer | 0 | 4 | 3 | False | 2 | True | neblig | 23.78 | 27.275 | 0.56 | 8.9981 |
| 2334 | sommer | 0 | 4 | 4 | False | 2 | True | neblig | 22.96 | 26.515 | 0.64 | 8.9981 |
| 2335 | sommer | 0 | 4 | 5 | False | 2 | True | neblig | 22.14 | 25.760 | 0.68 | 8.9981 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 12326 | sommer | 1 | 6 | 19 | False | 6 | False | klar | 26.24 | 31.060 | 0.36 | 11.0014 |
| 12327 | sommer | 1 | 6 | 20 | False | 6 | False | klar | 25.42 | 31.060 | 0.35 | 19.0012 |
| 12328 | sommer | 1 | 6 | 21 | False | 6 | False | klar | 24.60 | 31.060 | 0.40 | 7.0015 |
| 12329 | sommer | 1 | 6 | 22 | False | 6 | False | klar | 23.78 | 27.275 | 0.46 | 8.9981 |
| 12330 | sommer | 1 | 6 | 23 | False | 6 | False | klar | 22.96 | 26.515 | 0.52 | 7.0015 |
10000 Zeilen × 12 Spalten
Wir inspizieren nun den letzten Split
train_4, test_4 = all_splits[4]
X.iloc[test_4]
| saison | jahr | monat | stunde | feiertag | wochentag | arbeitstag | wetter | temp | gefuehlte_temp | feuchtigkeit | windgeschwindigkeit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16379 | winter | 1 | 11 | 5 | False | 2 | True | neblig | 13.94 | 16.665 | 0.66 | 8.9981 |
| 16380 | winter | 1 | 11 | 6 | False | 2 | True | neblig | 13.94 | 16.665 | 0.71 | 11.0014 |
| 16381 | winter | 1 | 11 | 7 | False | 2 | True | klar | 13.12 | 16.665 | 0.76 | 6.0032 |
| 16382 | winter | 1 | 11 | 8 | False | 2 | True | klar | 13.94 | 16.665 | 0.71 | 8.9981 |
| 16383 | winter | 1 | 11 | 9 | False | 2 | True | neblig | 14.76 | 18.940 | 0.71 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | fruehling | 1 | 12 | 19 | False | 1 | True | neblig | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | fruehling | 1 | 12 | 20 | False | 1 | True | neblig | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | fruehling | 1 | 12 | 21 | False | 1 | True | klar | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | fruehling | 1 | 12 | 22 | False | 1 | True | klar | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | fruehling | 1 | 12 | 23 | False | 1 | True | klar | 10.66 | 13.635 | 0.65 | 8.9981 |
1000 Zeilen × 12 Spalten
X.iloc[train_4]
| saison | jahr | monat | stunde | feiertag | wochentag | arbeitstag | wetter | temp | gefuehlte_temp | feuchtigkeit | windgeschwindigkeit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6331 | winter | 0 | 9 | 9 | False | 1 | True | neblig | 26.24 | 28.790 | 0.89 | 12.9980 |
| 6332 | winter | 0 | 9 | 10 | False | 1 | True | neblig | 26.24 | 28.790 | 0.89 | 12.9980 |
| 6333 | winter | 0 | 9 | 11 | False | 1 | True | klar | 27.88 | 31.820 | 0.79 | 15.0013 |
| 6334 | winter | 0 | 9 | 12 | False | 1 | True | neblig | 27.88 | 31.820 | 0.79 | 11.0014 |
| 6335 | winter | 0 | 9 | 13 | False | 1 | True | neblig | 28.70 | 33.335 | 0.74 | 11.0014 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 16326 | winter | 1 | 11 | 0 | False | 0 | False | neblig | 12.30 | 15.150 | 0.70 | 11.0014 |
| 16327 | winter | 1 | 11 | 1 | False | 0 | False | klar | 12.30 | 14.395 | 0.70 | 12.9980 |
| 16328 | winter | 1 | 11 | 2 | False | 0 | False | klar | 11.48 | 14.395 | 0.81 | 7.0015 |
| 16329 | winter | 1 | 11 | 3 | False | 0 | False | neblig | 12.30 | 15.150 | 0.81 | 11.0014 |
| 16330 | winter | 1 | 11 | 4 | False | 0 | False | neblig | 12.30 | 14.395 | 0.81 | 12.9980 |
10000 Zeilen × 12 Spalten
Alles bestens. Wir sind nun bereit, einige Vorhersagemodelle zu erstellen!
Gradient Boosting#
Gradient Boosting Regression mit Entscheidungsbäumen ist oft flexibel genug, um heterogene tabellarische Daten mit einer Mischung aus kategorialen und numerischen Merkmalen effizient zu verarbeiten, solange die Anzahl der Stichproben groß genug ist.
Hier verwenden wir den modernen HistGradientBoostingRegressor mit nativer Unterstützung für kategoriale Merkmale. Daher müssen wir nur categorical_features="from_dtype" setzen, damit Merkmale mit kategorialem `dtype` als kategoriale Merkmale betrachtet werden. Zur Referenz extrahieren wir die kategorialen Merkmale aus dem DataFrame basierend auf dem `dtype`. Die internen Bäume verwenden eine dedizierte Baumaufteilungsregel für diese Merkmale.
Die numerischen Variablen benötigen keine Vorverarbeitung und wir versuchen der Einfachheit halber nur die Standard-Hyperparameter für dieses Modell.
from sklearn.compose import ColumnTransformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import cross_validate
from sklearn.pipeline import make_pipeline
gbrt = HistGradientBoostingRegressor(categorical_features="from_dtype", random_state=42)
categorical_columns = X.columns[X.dtypes == "category"]
print("Categorical features:", categorical_columns.tolist())
Categorical features: ['season', 'holiday', 'workingday', 'weather']
Lassen Sie uns unser Gradient Boosting Modell mit dem mittleren absoluten Fehler der relativen Nachfrage bewerten, gemittelt über unsere 5 zeitbasierten Kreuzvalidierungs-Splits.
import numpy as np
def evaluate(model, X, y, cv, model_prop=None, model_step=None):
cv_results = cross_validate(
model,
X,
y,
cv=cv,
scoring=["neg_mean_absolute_error", "neg_root_mean_squared_error"],
return_estimator=model_prop is not None,
)
if model_prop is not None:
if model_step is not None:
values = [
getattr(m[model_step], model_prop) for m in cv_results["estimator"]
]
else:
values = [getattr(m, model_prop) for m in cv_results["estimator"]]
print(f"Mean model.{model_prop} = {np.mean(values)}")
mae = -cv_results["test_neg_mean_absolute_error"]
rmse = -cv_results["test_neg_root_mean_squared_error"]
print(
f"Mean Absolute Error: {mae.mean():.3f} +/- {mae.std():.3f}\n"
f"Root Mean Squared Error: {rmse.mean():.3f} +/- {rmse.std():.3f}"
)
evaluate(gbrt, X, y, cv=ts_cv, model_prop="n_iter_")
Mean model.n_iter_ = 100.0
Mean Absolute Error: 0.044 +/- 0.003
Root Mean Squared Error: 0.068 +/- 0.005
Wir sehen, dass wir max_iter groß genug gewählt haben, so dass ein frühes Stoppen stattgefunden hat.
Dieses Modell hat einen durchschnittlichen Fehler von etwa 4 bis 5 % der maximalen Nachfrage. Das ist ziemlich gut für einen ersten Versuch ohne Hyperparameter-Tuning! Wir mussten lediglich die kategorialen Merkmale explizit machen. Beachten Sie, dass die zeitbezogenen Merkmale unverändert übergeben werden, d.h. ohne Verarbeitung. Dies ist jedoch für baumartige Modelle kein großes Problem, da sie eine nicht-monotone Beziehung zwischen ordinalen Eingabemerkmalen und dem Ziel lernen können.
Dies ist bei linearen Regressionsmodellen nicht der Fall, wie wir im Folgenden sehen werden.
Naive lineare Regression#
Wie üblich für lineare Modelle müssen kategoriale Variablen One-Hot-enkodiert werden. Zur Konsistenz skalieren wir die numerischen Merkmale auf denselben 0-1-Bereich mit MinMaxScaler, obwohl dies in diesem Fall die Ergebnisse nicht stark beeinflusst, da sie bereits auf vergleichbaren Skalen liegen.
from sklearn.linear_model import RidgeCV
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
one_hot_encoder = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
alphas = np.logspace(-6, 6, 25)
naive_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(
naive_linear_pipeline, X, y, cv=ts_cv, model_prop="alpha_", model_step="ridgecv"
)
Mean model.alpha_ = 2.7298221281347037
Mean Absolute Error: 0.142 +/- 0.014
Root Mean Squared Error: 0.184 +/- 0.020
Es ist bestätigend zu sehen, dass das ausgewählte alpha_ in unserem angegebenen Bereich liegt.
Die Leistung ist nicht gut: Der durchschnittliche Fehler beträgt etwa 14 % der maximalen Nachfrage. Das ist mehr als dreimal so hoch wie der durchschnittliche Fehler des Gradient Boosting-Modells. Wir können vermuten, dass die naive ursprüngliche Kodierung (lediglich Min-Max-skaliert) der periodischen zeitbezogenen Merkmale das lineare Regressionsmodell daran hindert, die Zeitinformationen richtig zu nutzen: Die lineare Regression modelliert nicht automatisch nicht-monotone Beziehungen zwischen den Eingabemerkmalen und dem Ziel. Nichtlineare Terme müssen im Eingang konstruiert werden.
Zum Beispiel verhindert die rohe numerische Kodierung des Merkmals "stunde", dass das lineare Modell erkennt, dass eine Erhöhung der Stunde am Morgen von 6 auf 8 eine starke positive Auswirkung auf die Anzahl der Fahrradverleihungen haben sollte, während eine Erhöhung ähnlicher Größe am Abend von 18 auf 20 eine starke negative Auswirkung auf die vorhergesagte Anzahl der Fahrradverleihungen haben sollte.
Zeitpunkte als Kategorien#
Da die Zeitmerkmale diskret in ganzen Zahlen kodiert sind (24 eindeutige Werte im Merkmal "Stunden"), könnten wir uns entscheiden, diese als kategoriale Variablen mit One-Hot-Kodierung zu behandeln und dadurch jede Annahme zu ignorieren, die durch die Reihenfolge der Stundenwerte impliziert wird.
Die Verwendung von One-Hot-Kodierung für die Zeitmerkmale gibt dem linearen Modell viel mehr Flexibilität, da wir pro diskretem Zeitniveau ein zusätzliches Merkmal einführen.
one_hot_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.099 +/- 0.011
Root Mean Squared Error: 0.131 +/- 0.011
Die durchschnittliche Fehlerrate dieses Modells beträgt 10 %, was deutlich besser ist als die Verwendung der ursprünglichen (ordinalen) Kodierung des Zeitmerkmals. Dies bestätigt unsere Intuition, dass das lineare Regressionsmodell von der zusätzlichen Flexibilität profitiert, den Zeitverlauf nicht monoton zu behandeln.
Dies führt jedoch zu einer sehr großen Anzahl neuer Merkmale. Wenn die Tageszeit in Minuten seit Tagesbeginn anstelle von Stunden dargestellt würde, hätte die One-Hot-Kodierung 1440 Merkmale anstelle von 24 eingeführt. Dies könnte zu signifikanten Überanpassungen führen. Um dies zu vermeiden, könnten wir stattdessen sklearn.preprocessing.KBinsDiscretizer verwenden, um die Anzahl der Niveaus von fein-körnigen ordinalen oder numerischen Variablen neu zu binning, während wir dennoch von den nicht-monotonen Ausdrucksvorteilen der One-Hot-Kodierung profitieren.
Schließlich stellen wir auch fest, dass die One-Hot-Kodierung die Reihenfolge der Stundenstufen vollständig ignoriert, obwohl dies eine interessante induktive Voreingenommenheit sein könnte, die bis zu einem gewissen Grad beibehalten werden sollte. Im Folgenden versuchen wir, glatte, nicht-monotone Kodierungen zu untersuchen, die die relative Reihenfolge von Zeitmerkmalen lokal bewahren.
Trigonometrische Merkmale#
Als erster Versuch können wir versuchen, jedes dieser periodischen Merkmale mit einer Sinus- und Kosinustransformation mit der passenden Periode zu kodieren.
Jedes ordinale Zeitmerkmal wird in 2 Merkmale transformiert, die zusammen äquivalente Informationen auf nicht-monotone Weise kodieren, und was noch wichtiger ist, ohne Sprünge zwischen dem ersten und dem letzten Wert des periodischen Bereichs.
from sklearn.preprocessing import FunctionTransformer
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
Visualisieren wir die Auswirkung dieser Merkmalserweiterung auf synthetische Stundendaten mit etwas Extrapolation über Stunde=23 hinaus.
import pandas as pd
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("Trigonometric encoding for the 'hour' feature")
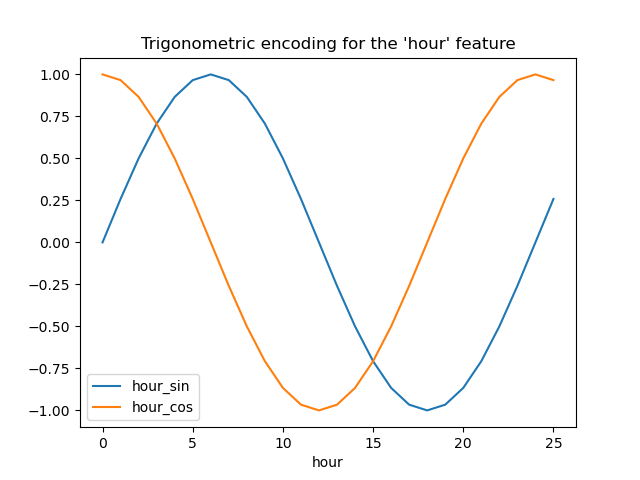
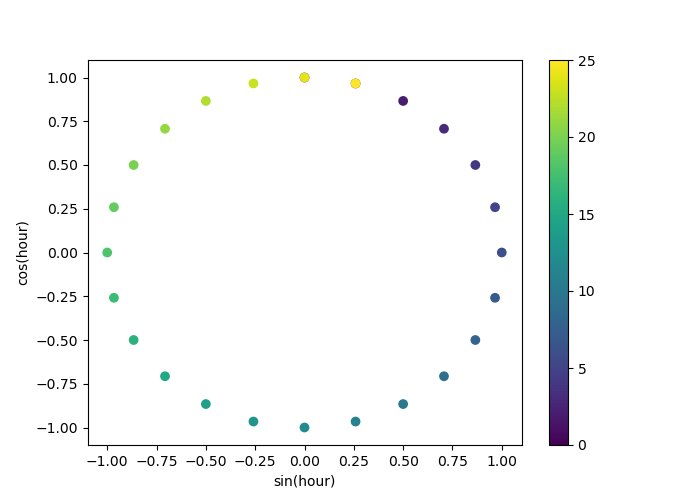
Verwenden wir ein 2D-Streudiagramm, bei dem die Stunden als Farben kodiert sind, um besser zu sehen, wie diese Darstellung die 24 Stunden des Tages in einem 2D-Raum abbildet, ähnlich einer Art 24-Stunden-Version einer Analoguhr. Beachten Sie, dass die "25." Stunde aufgrund der periodischen Natur der Sinus-/Kosinusdarstellung auf die 1. Stunde zurückgebildet wird.
fig, ax = plt.subplots(figsize=(7, 5))
sp = ax.scatter(hour_df["hour_sin"], hour_df["hour_cos"], c=hour_df["hour"])
ax.set(
xlabel="sin(hour)",
ylabel="cos(hour)",
)
_ = fig.colorbar(sp)
Wir können nun eine Pipeline zur Merkmalsextraktion mit dieser Strategie erstellen.
cyclic_cossin_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("month_sin", sin_transformer(12), ["month"]),
("month_cos", cos_transformer(12), ["month"]),
("weekday_sin", sin_transformer(7), ["weekday"]),
("weekday_cos", cos_transformer(7), ["weekday"]),
("hour_sin", sin_transformer(24), ["hour"]),
("hour_cos", cos_transformer(24), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_cossin_linear_pipeline = make_pipeline(
cyclic_cossin_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_cossin_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.125 +/- 0.014
Root Mean Squared Error: 0.166 +/- 0.020
Die Leistung unseres linearen Regressionsmodells mit diesem einfachen Feature Engineering ist etwas besser als bei der Verwendung der ursprünglichen ordinalen Zeitmerkmale, aber schlechter als bei der Verwendung der One-Hot-enkodierten Zeitmerkmale. Wir werden mögliche Gründe für dieses enttäuschende Ergebnis am Ende dieses Notebooks weiter analysieren.
Periodische Spline-Merkmale#
Wir können eine alternative Kodierung der periodischen zeitbezogenen Merkmale mit Spline-Transformationen mit einer ausreichend großen Anzahl von Splines versuchen, und als Ergebnis eine größere Anzahl von erweiterten Merkmalen im Vergleich zur Sinus/Kosinus-Transformation.
from sklearn.preprocessing import SplineTransformer
def periodic_spline_transformer(period, n_splines=None, degree=3):
if n_splines is None:
n_splines = period
n_knots = n_splines + 1 # periodic and include_bias is True
return SplineTransformer(
degree=degree,
n_knots=n_knots,
knots=np.linspace(0, period, n_knots).reshape(n_knots, 1),
extrapolation="periodic",
include_bias=True,
)
Visualisieren wir erneut die Auswirkung dieser Merkmalserweiterung auf synthetische Stundendaten mit etwas Extrapolation über Stunde=23 hinaus.
hour_df = pd.DataFrame(
np.linspace(0, 26, 1000).reshape(-1, 1),
columns=["hour"],
)
splines = periodic_spline_transformer(24, n_splines=12).fit_transform(hour_df)
splines_df = pd.DataFrame(
splines,
columns=[f"spline_{i}" for i in range(splines.shape[1])],
)
pd.concat([hour_df, splines_df], axis="columns").plot(x="hour", cmap=plt.cm.tab20b)
_ = plt.title("Periodic spline-based encoding for the 'hour' feature")
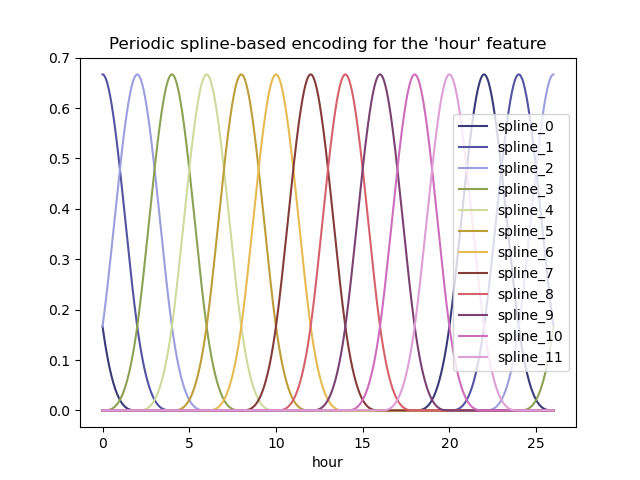
Dank der Verwendung des Parameters extrapolation="periodic" beobachten wir, dass die Merkmalskodierung bei der Extrapolation über Mitternacht hinaus glatt bleibt.
Wir können nun eine Vorhersagepipeline mit dieser alternativen periodischen Feature-Engineering-Strategie erstellen.
Es ist möglich, weniger Splines als diskrete Stufen für diese ordinalen Werte zu verwenden. Dies macht die Spline-basierte Kodierung effizienter als die One-Hot-Kodierung, während die meiste Ausdrucksstärke erhalten bleibt.
cyclic_spline_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("cyclic_month", periodic_spline_transformer(12, n_splines=6), ["month"]),
("cyclic_weekday", periodic_spline_transformer(7, n_splines=3), ["weekday"]),
("cyclic_hour", periodic_spline_transformer(24, n_splines=12), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_spline_linear_pipeline = make_pipeline(
cyclic_spline_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.097 +/- 0.011
Root Mean Squared Error: 0.132 +/- 0.013
Spline-Merkmale ermöglichen es dem linearen Modell, die periodischen zeitbezogenen Merkmale erfolgreich zu nutzen und den Fehler von ~14 % auf ~10 % der maximalen Nachfrage zu reduzieren, was dem ähnelt, was wir bei den One-Hot-enkodierten Merkmalen beobachtet haben.
Qualitative Analyse des Einflusses von Merkmalen auf lineare Modellvorhersagen#
Hier möchten wir den Einfluss der Feature-Engineering-Entscheidungen auf die zeitbezogene Form der Vorhersagen visualisieren.
Dazu betrachten wir einen beliebigen zeitbasierten Split, um die Vorhersagen auf einem Bereich von zurückgehaltenen Datenpunkten zu vergleichen.
naive_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
naive_linear_predictions = naive_linear_pipeline.predict(X.iloc[test_0])
one_hot_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_linear_predictions = one_hot_linear_pipeline.predict(X.iloc[test_0])
cyclic_cossin_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_cossin_linear_predictions = cyclic_cossin_linear_pipeline.predict(X.iloc[test_0])
cyclic_spline_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_linear_predictions = cyclic_spline_linear_pipeline.predict(X.iloc[test_0])
Wir visualisieren diese Vorhersagen, indem wir auf die letzten 96 Stunden (4 Tage) des Testdatensatzes zoomen, um qualitative Einblicke zu gewinnen.
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by linear models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(naive_linear_predictions[last_hours], "x-", label="Ordinal time features")
ax.plot(
cyclic_cossin_linear_predictions[last_hours],
"x-",
label="Trigonometric time features",
)
ax.plot(
cyclic_spline_linear_predictions[last_hours],
"x-",
label="Spline-based time features",
)
ax.plot(
one_hot_linear_predictions[last_hours],
"x-",
label="One-hot time features",
)
_ = ax.legend()
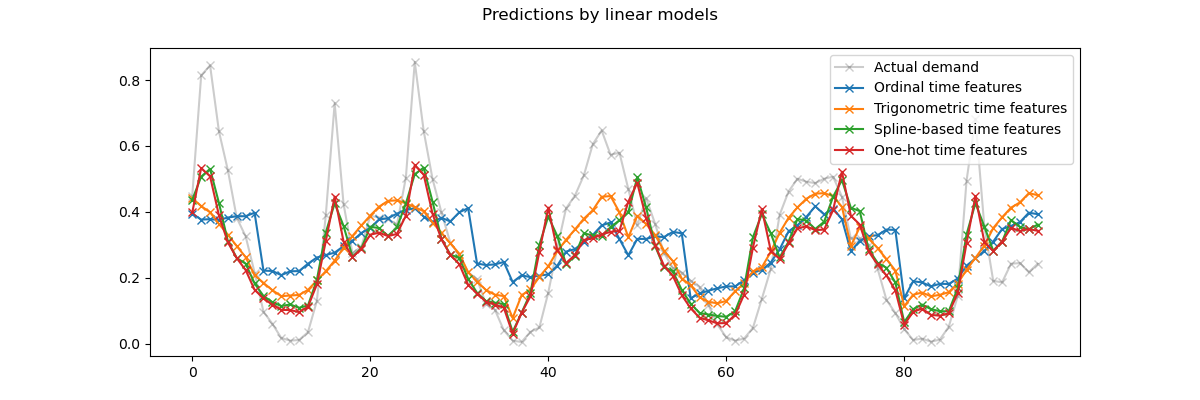
Aus der obigen Abbildung können wir folgende Schlussfolgerungen ziehen:
Die rohen ordinalen zeitbezogenen Merkmale sind problematisch, da sie die natürliche Periodizität nicht erfassen: Wir beobachten einen großen Sprung in den Vorhersagen am Ende jedes Tages, wenn die Stundenmerkmale von 23 auf 0 wechseln. Wir können ähnliche Artefakte am Ende jeder Woche oder jedes Jahres erwarten.
Wie erwartet, haben die trigonometrischen Merkmale (Sinus und Kosinus) keine solchen Diskontinuitäten um Mitternacht, aber das lineare Regressionsmodell versagt dabei, diese Merkmale zu nutzen, um Tagesvariationen richtig zu modellieren. Die Verwendung trigonometrischer Merkmale für höhere Harmonische oder zusätzliche trigonometrische Merkmale für die natürliche Periode mit unterschiedlichen Phasen könnte dieses Problem potenziell beheben.
Die periodischen Spline-basierten Merkmale beheben diese beiden Probleme gleichzeitig: Sie verleihen dem linearen Modell mehr Ausdrucksstärke, indem sie es ermöglichen, sich dank der Verwendung von 12 Splines auf bestimmte Stunden zu konzentrieren. Darüber hinaus erzwingt die Option
extrapolation="periodic"eine glatte Darstellung zwischenStunde=23undStunde=0.Die One-Hot-enkodierten Merkmale verhalten sich ähnlich wie die periodischen Spline-basierten Merkmale, sind aber spitzer: Sie können beispielsweise den Morgenansturm an Arbeitstagen besser modellieren, da dieser Anstieg kürzer als eine Stunde dauert. Wir werden jedoch im Folgenden sehen, dass das, was für lineare Modelle ein Vorteil sein kann, nicht unbedingt auch für ausdrucksstärkere Modelle gilt.
Wir können auch die Anzahl der Merkmale vergleichen, die von jeder Feature-Engineering-Pipeline extrahiert werden.
naive_linear_pipeline[:-1].transform(X).shape
(17379, 19)
one_hot_linear_pipeline[:-1].transform(X).shape
(17379, 59)
cyclic_cossin_linear_pipeline[:-1].transform(X).shape
(17379, 22)
cyclic_spline_linear_pipeline[:-1].transform(X).shape
(17379, 37)
Dies bestätigt, dass die One-Hot-Kodierungs- und die Spline-Kodierungsstrategien viel mehr Merkmale für die Zeitrepräsentation erzeugen als die Alternativen, was dem nachgeschalteten linearen Modell mehr Flexibilität (Freiheitsgrade) zur Vermeidung von Unteranpassung gibt.
Abschließend stellen wir fest, dass keines der linearen Modelle die tatsächliche Fahrradverleihnachfrage annähern kann, insbesondere bei Spitzen, die zu Stoßzeiten an Arbeitstagen sehr scharf sein können, an Wochenenden jedoch viel flacher sind: Die genauesten linearen Modelle, die auf Splines oder One-Hot-Kodierung basieren, neigen dazu, Spitzen von Pendlerfahrradverleihungen auch an Wochenenden vorherzusagen und Pendlerereignisse an Arbeitstagen zu unterschätzen.
Diese systematischen Vorhersagefehler deuten auf eine Form der Unteranpassung hin und können durch das Fehlen von Interaktionstermen zwischen Merkmalen erklärt werden, z.B. „Arbeitstag“ und Merkmale, die aus „Stunden“ abgeleitet sind. Dieses Problem wird im folgenden Abschnitt behandelt.
Modellierung von paarweisen Interaktionen mit Splines und Polynom-Merkmalen#
Lineare Modelle erfassen keine Interaktionseffekte zwischen Eingabemerkmalen automatisch. Es hilft nicht, dass einige Merkmale marginal nichtlinear sind, wie es bei Merkmalen der Fall ist, die von SplineTransformer (oder One-Hot-Kodierung oder Binning) konstruiert werden.
Es ist jedoch möglich, die Klasse PolynomialFeatures auf grob körnig Spline-enkodierten Stunden anzuwenden, um die Interaktion „Arbeitstag“/„Stunden“ explizit zu modellieren, ohne zu viele neue Variablen einzuführen.
from sklearn.pipeline import FeatureUnion
from sklearn.preprocessing import PolynomialFeatures
hour_workday_interaction = make_pipeline(
ColumnTransformer(
[
("cyclic_hour", periodic_spline_transformer(24, n_splines=8), ["hour"]),
("workingday", FunctionTransformer(lambda x: x == "True"), ["workingday"]),
]
),
PolynomialFeatures(degree=2, interaction_only=True, include_bias=False),
)
Diese Merkmale werden dann mit den bereits in der vorherigen Spline-basierten Pipeline berechneten kombiniert. Wir können eine schöne Leistungsverbesserung beobachten, indem wir diese paarweise Interaktion explizit modellieren.
cyclic_spline_interactions_pipeline = make_pipeline(
FeatureUnion(
[
("marginal", cyclic_spline_transformer),
("interactions", hour_workday_interaction),
]
),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_interactions_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.078 +/- 0.009
Root Mean Squared Error: 0.104 +/- 0.009
Modellierung nichtlinearer Merkmalsinteraktionen mit Kerneln#
Die vorherige Analyse hob die Notwendigkeit hervor, die Interaktionen zwischen "arbeitstag" und "stunden" zu modellieren. Ein weiteres Beispiel für eine solche nichtlineare Interaktion, die wir modellieren möchten, könnte der Einfluss von Regen sein, der sich beispielsweise an Arbeitstagen und an Wochenenden und Feiertagen unterscheiden könnte.
Um all solche Interaktionen zu modellieren, könnten wir entweder eine polynomische Expansion auf alle marginalen Merkmale auf einmal anwenden, nachdem sie Spline-basiert erweitert wurden. Dies würde jedoch eine quadratische Anzahl von Merkmalen erzeugen, was zu Überanpassung und Problemen bei der rechnerischen Handhabbarkeit führen kann.
Alternativ können wir die Nyström-Methode verwenden, um eine ungefähre polynomische Kernel-Expansion zu berechnen. Versuchen wir Letzteres.
from sklearn.kernel_approximation import Nystroem
cyclic_spline_poly_pipeline = make_pipeline(
cyclic_spline_transformer,
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.053 +/- 0.002
Root Mean Squared Error: 0.076 +/- 0.004
Wir beobachten, dass dieses Modell der Leistung von Gradient-Boosted Trees mit einem durchschnittlichen Fehler von etwa 5 % der maximalen Nachfrage fast ebenbürtig ist.
Beachten Sie, dass, obwohl der letzte Schritt dieser Pipeline ein lineares Regressionsmodell ist, die Zwischenschritte wie die Spline-Merkmalsextraktion und die Nyström-Kernel-Approximation hochgradig nichtlinear sind. Infolgedessen ist die kombinierte Pipeline ausdrucksstärker als ein einfaches lineares Regressionsmodell mit Rohmerkmalen.
Zur Vollständigkeit bewerten wir auch die Kombination von One-Hot-Kodierung und Kernel-Approximation.
one_hot_poly_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder="passthrough",
),
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.082 +/- 0.006
Root Mean Squared Error: 0.111 +/- 0.011
Während One-Hot-enkodierte Merkmale bei der Verwendung linearer Modelle wettbewerbsfähig mit Spline-basierten Merkmalen waren, ist dies bei Verwendung einer Rang-niedrigen Approximation eines nichtlinearen Kernels nicht mehr der Fall: Dies kann erklärt werden, indem Spline-Merkmale glatter sind und der Kernel-Approximation ermöglichen, eine ausdrucksstärkere Entscheidungsfunktion zu finden.
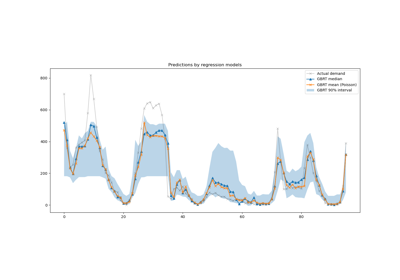
Betrachten wir nun qualitativ die Vorhersagen der Kernel-Modelle und der Gradient-Boosted Trees, die in der Lage sein sollten, nichtlineare Interaktionen zwischen Merkmalen besser zu modellieren.
gbrt.fit(X.iloc[train_0], y.iloc[train_0])
gbrt_predictions = gbrt.predict(X.iloc[test_0])
one_hot_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_poly_predictions = one_hot_poly_pipeline.predict(X.iloc[test_0])
cyclic_spline_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_poly_predictions = cyclic_spline_poly_pipeline.predict(X.iloc[test_0])
Auch hier zoomen wir auf die letzten 4 Tage des Testdatensatzes.
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by non-linear regression models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
gbrt_predictions[last_hours],
"x-",
label="Gradient Boosted Trees",
)
ax.plot(
one_hot_poly_predictions[last_hours],
"x-",
label="One-hot + polynomial kernel",
)
ax.plot(
cyclic_spline_poly_predictions[last_hours],
"x-",
label="Splines + polynomial kernel",
)
_ = ax.legend()
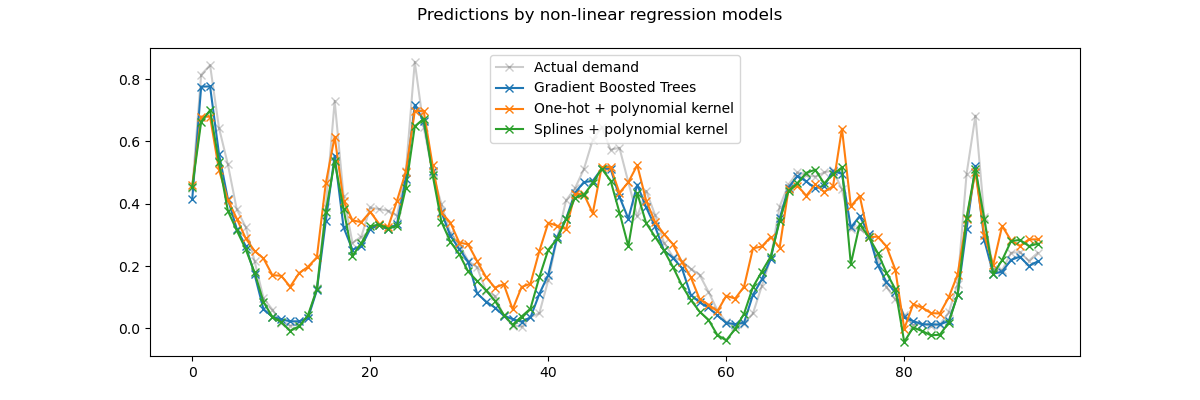
Erstens, beachten Sie, dass Bäume nichtlineare Merkmalsinteraktionen natürlich modellieren können, da Entscheidungsbäume standardmäßig über eine Tiefe von 2 Ebenen hinaus wachsen dürfen.
Hier können wir beobachten, dass die Kombination von Spline-Merkmalen und nichtlinearen Kerneln recht gut funktioniert und fast an die Genauigkeit von Gradient Boosting-Regressionsbäumen heranreicht.
Im Gegensatz dazu schneiden One-Hot-enkodierte Zeitmerkmale mit dem Rang-niedrigen Kernel-Modell nicht so gut ab. Insbesondere überschätzen sie die geringe Nachfrage stundenlang deutlich stärker als konkurrierende Modelle.
Wir stellen auch fest, dass keines der Modelle einige der Spitzen-Mietpreise zu den Stoßzeiten an Arbeitstagen erfolgreich vorhersagen kann. Möglicherweise wären zusätzliche Merkmale erforderlich, um die Genauigkeit der Vorhersagen weiter zu verbessern. Beispielsweise könnte es nützlich sein, Zugang zur geografischen Verteilung der Flotte zu jeder Zeit zu haben oder zum Anteil der Fahrräder, die aufgrund von Wartungsbedarf immobilisiert sind.
Werfen wir schließlich einen quantitativeren Blick auf die Vorhersagefehler dieser drei Modelle mithilfe der Scatterplots von tatsächlicher vs. vorhergesagter Nachfrage.
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(13, 7), sharex=True, sharey="row")
fig.suptitle("Non-linear regression models", y=1.0)
predictions = [
one_hot_poly_predictions,
cyclic_spline_poly_predictions,
gbrt_predictions,
]
labels = [
"One hot +\npolynomial kernel",
"Splines +\npolynomial kernel",
"Gradient Boosted\nTrees",
]
plot_kinds = ["actual_vs_predicted", "residual_vs_predicted"]
for axis_idx, kind in enumerate(plot_kinds):
for ax, pred, label in zip(axes[axis_idx], predictions, labels):
disp = PredictionErrorDisplay.from_predictions(
y_true=y.iloc[test_0],
y_pred=pred,
kind=kind,
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set_xticks(np.linspace(0, 1, num=5))
if axis_idx == 0:
ax.set_yticks(np.linspace(0, 1, num=5))
ax.legend(
["Best model", label],
loc="upper center",
bbox_to_anchor=(0.5, 1.3),
ncol=2,
)
ax.set_aspect("equal", adjustable="box")
plt.show()
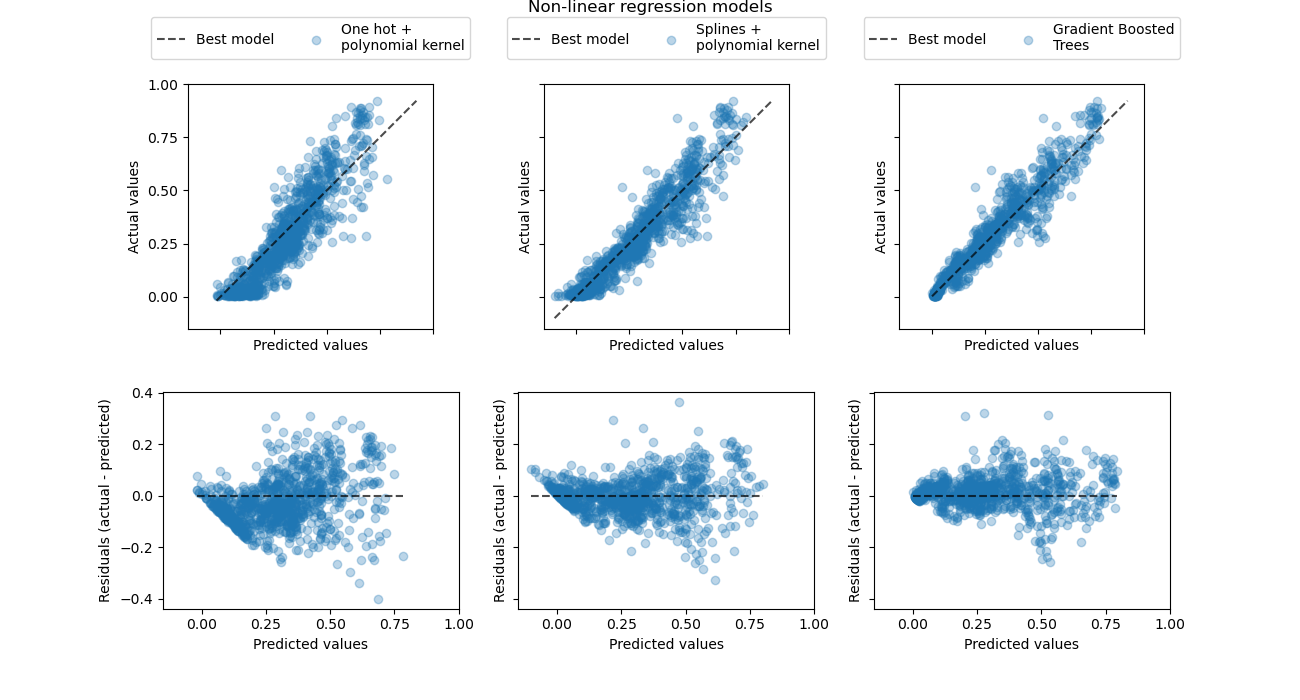
Diese Visualisierung bestätigt die Schlussfolgerungen, die wir aus der vorherigen Abbildung gezogen haben.
Alle Modelle unterschätzen die Ereignisse mit hoher Nachfrage (Stoßzeiten an Arbeitstagen), aber Gradient Boosting etwas weniger. Die Ereignisse mit geringer Nachfrage werden im Durchschnitt gut von Gradient Boosting vorhergesagt, während die One-Hot-Polynomial-Regression-Pipeline in diesem Bereich systematisch die Nachfrage überschätzt. Insgesamt sind die Vorhersagen der Gradient-Boosted Trees näher an der Diagonalen als bei den Kernel-Modellen.
Schlussbemerkungen#
Wir stellen fest, dass wir für Kernel-Modelle geringfügig bessere Ergebnisse erzielen könnten, indem wir mehr Komponenten (höherrangige Kernel-Approximation) verwenden, auf Kosten längerer Anpassungs- und Vorhersagezeiten. Bei großen Werten von n_components würde die Leistung der One-Hot-enkodierten Merkmale sogar die Spline-Merkmale erreichen.
Der Regressor Nystroem + RidgeCV könnte auch durch MLPRegressor mit einem oder zwei versteckten Schichten ersetzt werden und wir hätten ziemlich ähnliche Ergebnisse erzielt.
Der in diesem Fall verwendete Datensatz wird stündlich erfasst. Zyklische Spline-basierte Merkmale könnten jedoch die Tageszeit oder die Wochezeitt sehr effizient mit feinkörnigeren Zeitauflösungen (z. B. mit Messungen alle Minute anstelle jeder Stunde) modellieren, ohne mehr Merkmale einzuführen. One-Hot-Kodierungszeitrepräsentationen würden diese Flexibilität nicht bieten.
Schließlich haben wir in diesem Notebook RidgeCV verwendet, da es rechnerisch sehr effizient ist. Es modelliert jedoch die Zielvariable als eine Gaußsche Zufallsvariable mit konstanter Varianz. Bei positiven Regressionsproblemen ist es wahrscheinlich sinnvoller, eine Poisson- oder Gamma-Verteilung zu verwenden. Dies könnte durch die Verwendung von GridSearchCV(TweedieRegressor(power=2), param_grid({"alpha": alphas})) anstelle von RidgeCV erreicht werden.
Gesamte Laufzeit des Skripts: (0 Minuten 15,109 Sekunden)
Verwandte Beispiele

Unterstützung für kategorische Merkmale in Gradient Boosting