Receiver Operating Characteristic (ROC) mit Kreuzvalidierung

Dieses Beispiel zeigt, wie die Varianz der Receiver Operating Characteristic (ROC)-Metrik mithilfe der Kreuzvalidierung geschätzt und visualisiert werden kann.

ROC-Kurven stellen typischerweise die True Positive Rate (TPR) auf der Y-Achse und die False Positive Rate (FPR) auf der X-Achse dar. Das bedeutet, dass die obere linke Ecke des Plots der „ideale“ Punkt ist – eine FPR von Null und eine TPR von Eins. Dies ist nicht sehr realistisch, bedeutet aber, dass eine größere Fläche unter der Kurve (AUC) normalerweise besser ist. Die „Steilheit“ von ROC-Kurven ist ebenfalls wichtig, da es ideal ist, die TPR zu maximieren und gleichzeitig die FPR zu minimieren.

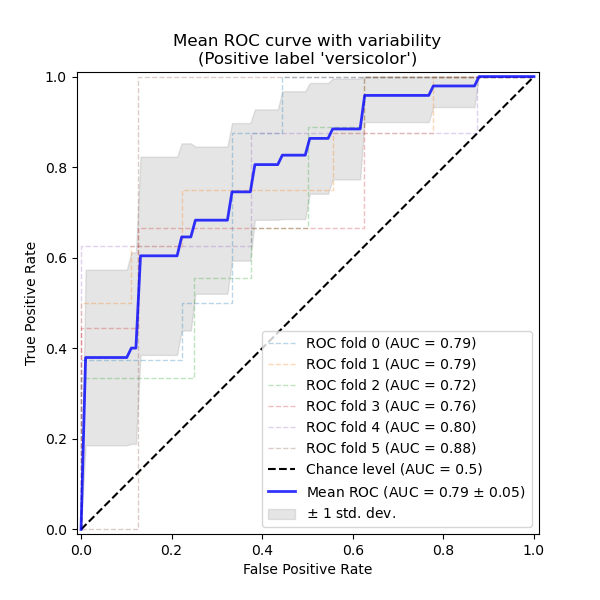
Dieses Beispiel zeigt die ROC-Antwort verschiedener Datensätze, die aus K-Fold-Kreuzvalidierung erstellt wurden. Aus all diesen Kurven ist es möglich, die mittlere AUC zu berechnen und die Varianz der Kurve zu sehen, wenn der Trainingssatz in verschiedene Teilmengen aufgeteilt wird. Dies zeigt grob, wie die Klassifikatorausgabe durch Änderungen in den Trainingsdaten beeinflusst wird und wie unterschiedlich die durch K-Fold-Kreuzvalidierung erzeugten Teilungen voneinander sind.

Hinweis

Siehe Multiklassen Receiver Operating Characteristic (ROC) für eine Ergänzung dieses Beispiels, die die Durchschnittsstrategien zur Verallgemeinerung der Metriken für Multiklassen-Klassifikatoren erklärt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Daten laden und vorbereiten

Wir importieren den Iris-Datensatz, der 3 Klassen enthält, die jeweils einem Typ von Iris-Pflanze entsprechen. Eine Klasse ist linear von den anderen 2 trennbar; die letzteren sind nicht linear voneinander trennbar.

Im Folgenden binarisieren wir den Datensatz, indem wir die Klasse „virginica“ (class_id=2) verwerfen. Dies bedeutet, dass die Klasse „versicolor“ (class_id=1) als positive Klasse und „setosa“ als negative Klasse (class_id=0) betrachtet wird.

import numpy as np

from sklearn.datasets import load_iris

iris = load_iris()
target_names = iris.target_names
X, y = iris.data, iris.target
X, y = X[y != 2], y[y != 2]
n_samples, n_features = X.shape

Wir fügen auch verrauschte Merkmale hinzu, um das Problem zu erschweren.

random_state = np.random.RandomState(0)
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)

Klassifizierung und ROC-Analyse

Hier führen wir cross_validate auf einem SVC-Klassifikator aus und verwenden dann die berechneten Kreuzvalidierungsergebnisse, um die ROC-Kurven fold-weise zu plotten. Beachten Sie, dass die Basislinie zur Definition des Zufallsniveaus (gestrichelte ROC-Kurve) ein Klassifikator ist, der immer die häufigste Klasse vorhersagen würde.

import matplotlib.pyplot as plt

from sklearn import svm
from sklearn.metrics import RocCurveDisplay, auc
from sklearn.model_selection import StratifiedKFold, cross_validate

n_splits = 6
cv = StratifiedKFold(n_splits=n_splits)
classifier = svm.SVC(kernel="linear", probability=True, random_state=random_state)
cv_results = cross_validate(
    classifier, X, y, cv=cv, return_estimator=True, return_indices=True
)

prop_cycle = plt.rcParams["axes.prop_cycle"]
colors = prop_cycle.by_key()["color"]
curve_kwargs_list = [
    dict(alpha=0.3, lw=1, color=colors[fold % len(colors)]) for fold in range(n_splits)
]
names = [f"ROC fold {idx}" for idx in range(n_splits)]

mean_fpr = np.linspace(0, 1, 100)
interp_tprs = []

_, ax = plt.subplots(figsize=(6, 6))
viz = RocCurveDisplay.from_cv_results(
    cv_results,
    X,
    y,
    ax=ax,
    name=names,
    curve_kwargs=curve_kwargs_list,
    plot_chance_level=True,
)

for idx in range(n_splits):
    interp_tpr = np.interp(mean_fpr, viz.fpr[idx], viz.tpr[idx])
    interp_tpr[0] = 0.0
    interp_tprs.append(interp_tpr)

mean_tpr = np.mean(interp_tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(viz.roc_auc)

ax.plot(
    mean_fpr,
    mean_tpr,
    color="b",
    label=r"Mean ROC (AUC = %0.2f $\pm$ %0.2f)" % (mean_auc, std_auc),
    lw=2,
    alpha=0.8,
)

std_tpr = np.std(interp_tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
ax.fill_between(
    mean_fpr,
    tprs_lower,
    tprs_upper,
    color="grey",
    alpha=0.2,
    label=r"$\pm$ 1 std. dev.",
)

ax.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title=f"Mean ROC curve with variability\n(Positive label '{target_names[1]}')",
)
ax.legend(loc="lower right")
plt.show()

Verwandte Beispiele

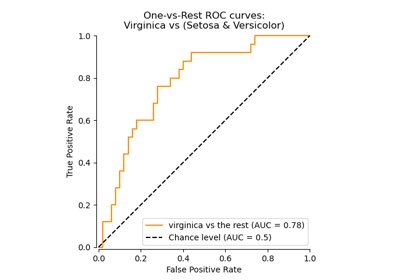
Multiklassen-Receiver Operating Characteristic (ROC)

Multiklassen-Receiver Operating Characteristic (ROC)

ROC-Kurve mit Visualisierungs-API

ROC-Kurve mit Visualisierungs-API

Detection Error Tradeoff (DET) Kurve

Detection Error Tradeoff (DET) Kurve

Multi-Klassen SGD auf dem Iris-Datensatz plotten

Multi-Klassen SGD auf dem Iris-Datensatz plotten