Vergleich der Kalibrierung von Klassifikatoren

Gut kalibrierte Klassifikatoren sind probabilistische Klassifikatoren, bei denen die Ausgabe von predict_proba direkt als Konfidenzniveau interpretiert werden kann. Ein gut kalibrierter (binärer) Klassifikator sollte beispielsweise die Samples so klassifizieren, dass für die Samples, denen er einen predict_proba-Wert nahe 0,8 zuweist, tatsächlich etwa 80 % zur positiven Klasse gehören.

In diesem Beispiel vergleichen wir die Kalibrierung von vier verschiedenen Modellen: Logistische Regression, Gaussian Naive Bayes, Random Forest Classifier und Linear SVM.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatz

Wir verwenden ein synthetisches binäres Klassifizierungsdatenset mit 100.000 Samples und 20 Merkmalen. Von den 20 Merkmalen sind nur 2 informativ, 2 sind redundant (zufällige Kombinationen der informativen Merkmale) und die restlichen 16 sind uninteressant (zufällige Zahlen).

Von den 100.000 Samples werden 100 zur Modell-Anpassung und die restlichen zum Testen verwendet. Beachten Sie, dass diese Aufteilung recht ungewöhnlich ist: Ziel ist es, stabile Kalibrierungskurven-Schätzungen für Modelle zu erhalten, die potenziell zu Überanpassung neigen. In der Praxis sollte man eher eine Kreuzvalidierung mit ausgewogeneren Aufteilungen verwenden, aber das würde den Code dieses Beispiels komplizierter machen.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100_000, n_features=20, n_informative=2, n_redundant=2, random_state=42
)

train_samples = 100  # Samples used for training the models
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    shuffle=False,
    test_size=100_000 - train_samples,
)

Kalibrierungskurven

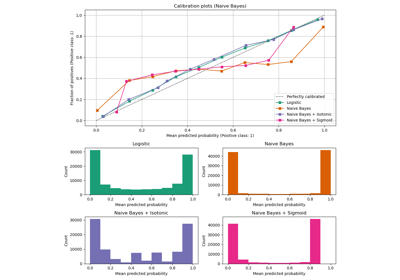
Unten trainieren wir jedes der vier Modelle mit dem kleinen Trainingsdatenset und plottet dann Kalibrierungskurven (auch Zuverlässigkeitsdiagramme genannt) unter Verwendung der vorhergesagten Wahrscheinlichkeiten des Testdatensets. Kalibrierungskurven werden erstellt, indem die vorhergesagten Wahrscheinlichkeiten in Bins eingeteilt werden, dann die mittlere vorhergesagte Wahrscheinlichkeit in jedem Bin gegen die beobachtete Häufigkeit („Anteil der positiven Fälle“) geplottet wird. Unter der Kalibrierungskurve plotten wir ein Histogramm, das die Verteilung der vorhergesagten Wahrscheinlichkeiten zeigt, oder genauer gesagt, die Anzahl der Samples in jedem Bin der vorhergesagten Wahrscheinlichkeit.

import numpy as np

from sklearn.svm import LinearSVC


class NaivelyCalibratedLinearSVC(LinearSVC):
    """LinearSVC with `predict_proba` method that naively scales
    `decision_function` output."""

    def fit(self, X, y):
        super().fit(X, y)
        df = self.decision_function(X)
        self.df_min_ = df.min()
        self.df_max_ = df.max()

    def predict_proba(self, X):
        """Min-max scale output of `decision_function` to [0,1]."""
        df = self.decision_function(X)
        calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
        proba_pos_class = np.clip(calibrated_df, 0, 1)
        proba_neg_class = 1 - proba_pos_class
        proba = np.c_[proba_neg_class, proba_pos_class]
        return proba

from sklearn.calibration import CalibrationDisplay
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegressionCV
from sklearn.naive_bayes import GaussianNB

# Define the classifiers to be compared in the study.
#
# Note that we use a variant of the logistic regression model that can
# automatically tune its regularization parameter.
#
# For a fair comparison, we should run a hyper-parameter search for all the
# classifiers but we don't do it here for the sake of keeping the example code
# concise and fast to execute.
lr = LogisticRegressionCV(
    Cs=np.logspace(-6, 6, 101),
    cv=10,
    l1_ratios=(0,),
    scoring="neg_log_loss",
    max_iter=1_000,
    use_legacy_attributes=False,
)
gnb = GaussianNB()
svc = NaivelyCalibratedLinearSVC(C=1.0)
rfc = RandomForestClassifier(random_state=42)

clf_list = [
    (lr, "Logistic Regression"),
    (gnb, "Naive Bayes"),
    (svc, "SVC"),
    (rfc, "Random forest"),
]

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
markers = ["^", "v", "s", "o"]
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
        marker=markers[i],
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots")

# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")

plt.tight_layout()
plt.show()

Analyse der Ergebnisse

LogisticRegressionCV liefert trotz der kleinen Trainingsdatensatzgröße einigermaßen gut kalibrierte Vorhersagen: Ihre Zuverlässigkeitskurve liegt am nächsten zur Diagonalen unter den vier Modellen.

Die logistische Regression wird durch Minimierung des Log-Loss trainiert, was eine strikt richtige Bewertungsregel ist: Im Grenzfall unendlich vieler Trainingsdaten werden strikt richtige Bewertungsregeln durch das Modell minimiert, das die wahren bedingten Wahrscheinlichkeiten vorhersagt. Dieses (hypothetische) Modell wäre daher perfekt kalibriert. Die Verwendung einer richtigen Bewertungsregel als Trainingsziel reicht jedoch nicht aus, um ein gut kalibriertes Modell zu garantieren: Selbst mit einem sehr großen Trainingsdatensatz kann die logistische Regression schlecht kalibriert bleiben, wenn sie zu stark regularisiert wurde oder wenn die Wahl und Vorverarbeitung der Eingabemerkmale dieses Modell falsch spezifizierte (z. B. wenn die wahre Entscheidungsgrenze des Datensatzes eine stark nichtlineare Funktion der Eingabemerkmale ist).

In diesem Beispiel wurde der Trainingsdatensatz absichtlich sehr klein gehalten. In dieser Situation kann die Optimierung des Log-Loss aufgrund von Überanpassung immer noch zu schlecht kalibrierten Modellen führen. Um dem entgegenzuwirken, wurde die Klasse LogisticRegressionCV so konfiguriert, dass der C-Regularisierungsparameter optimiert wird, um den Log-Loss auch über innere Kreuzvalidierung zu minimieren, um den besten Kompromiss für dieses Modell in der Umgebung mit kleinen Trainingsdatensätzen zu finden.

Aufgrund der endlichen Größe des Trainingsdatensatzes und des Fehlens einer Garantie für eine korrekte Spezifikation beobachten wir, dass die Kalibrierungskurve des Modells der logistischen Regression nahe an der Diagonalen liegt, aber nicht perfekt darauf. Die Form der Kalibrierungskurve dieses Modells kann als leicht unterkonfident interpretiert werden: Die vorhergesagten Wahrscheinlichkeiten liegen etwas zu nahe bei 0,5 im Vergleich zum tatsächlichen Anteil der positiven Samples.

Die anderen Methoden geben alle weniger gut kalibrierte Wahrscheinlichkeiten aus

• GaussianNB neigt dazu, Wahrscheinlichkeiten auf 0 oder 1 zu verschieben (siehe Histogramm) bei diesem speziellen Datensatz (Überkonfidenz). Dies liegt hauptsächlich daran, dass die Naive Bayes-Gleichung nur dann korrekte Wahrscheinlichkeits-Schätzungen liefert, wenn die Annahme der bedingten Unabhängigkeit der Merkmale gilt [2]. Merkmale können jedoch korreliert sein, und das ist bei diesem Datensatz der Fall, der 2 Merkmale enthält, die als zufällige Linearkombinationen der informativen Merkmale generiert wurden. Diese korrelierten Merkmale werden effektiv „doppelt gezählt“, was dazu führt, dass die vorhergesagten Wahrscheinlichkeiten in Richtung 0 und 1 verschoben werden [3]. Beachten Sie jedoch, dass das Ändern des für die Generierung des Datensatzes verwendeten Seeds zu weitgehend unterschiedlichen Ergebnissen für den Naive Bayes-Schätzer führen kann.

• LinearSVC ist kein natürlicher probabilistischer Klassifikator. Um seine Vorhersage als solche interpretieren zu können, haben wir die Ausgabe der decision_function naiv in [0, 1] skaliert, indem wir Min-Max-Skalierung in der oben definierten Wrapper-Klasse NaivelyCalibratedLinearSVC angewendet haben. Dieser Schätzer zeigt auf diesen Daten eine typische sigmoidförmige Kalibrierungskurve: Vorhersagen größer als 0,5 entsprechen Samples mit einem noch größeren effektiven positiven Klassenanteil (oberhalb der Diagonalen), während Vorhersagen unter 0,5 sogar noch geringeren positiven Klassenanteilen entsprechen (unterhalb der Diagonalen). Diese unterkonfidenten Vorhersagen sind typisch für Maximum-Margin-Methoden [1].

• RandomForestClassifiers Vorhersagehistogramm zeigt Spitzen bei ca. 0,2 und 0,9 Wahrscheinlichkeit, während Wahrscheinlichkeiten nahe 0 oder 1 sehr selten sind. Eine Erklärung dafür gibt [1]: „Methoden wie Bagging und Random Forests, die Vorhersagen von einer Basismenge von Modellen mitteln, können Schwierigkeiten haben, Vorhersagen nahe 0 und 1 zu treffen, da die Varianz in den zugrunde liegenden Basismodellen Vorhersagen, die nahe Null oder Eins sein sollten, von diesen Werten weg verschieben kann. Da die Vorhersagen auf das Intervall [0, 1] beschränkt sind, sind Fehler, die durch Varianz verursacht werden, nahe Null und Eins tendenziell einseitig. Wenn beispielsweise ein Modell für einen Fall p = 0 vorhersagen sollte, kann Bagging dies nur erreichen, wenn alle Bagging-Bäume Null vorhersagen. Wenn wir Rauschen zu den Bäumen hinzufügen, über die Bagging mittelt, führt dieses Rauschen dazu, dass einige Bäume für diesen Fall Werte größer als 0 vorhersagen, wodurch die durchschnittliche Vorhersage des Bagging-Ensembles von Null weg verschoben wird. Wir beobachten diesen Effekt am stärksten bei Random Forests, da die Bäume der Basisebene, die mit Random Forests trainiert werden, aufgrund der Merkmalsunterteilung eine relativ hohe Varianz aufweisen.“ Dieser Effekt kann Random Forests unterkonfident machen. Trotz dieser möglichen Verzerrung ist zu beachten, dass die Bäume selbst durch Minimierung des Gini- oder Entropiekriteriums angepasst werden, was beides zu Splits führt, die korrekte Bewertungsregeln minimieren: den Brier-Score bzw. den Log-Loss. Weitere Details finden Sie im Benutzerhandbuch. Dies kann erklären, warum dieses Modell bei diesem speziellen Beispiel-Datensatz eine ausreichend gute Kalibrierungskurve aufweist. Tatsächlich ist das Random Forest-Modell nicht signifikant unterkonfidenter als das Logistische Regression-Modell.

Führen Sie dieses Beispiel gerne mit verschiedenen Zufallssamen und anderen Parametern zur Datensatzgenerierung erneut aus, um zu sehen, wie unterschiedlich die Kalibrierungsdiagramme aussehen können. Im Allgemeinen tendieren logistische Regression und Random Forest dazu, die am besten kalibrierten Klassifikatoren zu sein, während SVC oft die typische unterkonfidente Fehlkalibrierung aufweist. Das Naive Bayes-Modell ist ebenfalls oft schlecht kalibriert, aber die allgemeine Form seiner Kalibrierungskurve kann je nach Datensatz stark variieren.

Beachten Sie abschließend, dass bei einigen Datensatz-Seeds alle Modelle schlecht kalibriert sind, selbst wenn die Regularisierungsparameter wie oben optimiert werden. Dies ist unvermeidlich, wenn die Trainingsgröße zu klein ist oder das Modell stark fehlspezifiziert ist.

Referenzen

[1] (1,2)

Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005

[2]

Beyond independence: Conditions for the optimality of the simple Bayesian classifier Domingos, P., & Pazzani, M., Proc. 13th Intl. Conf. Machine Learning. 1996.

[3]

Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers Zadrozny, Bianca, and Charles Elkan. Icml. Vol. 1. 2001.

Verwandte Beispiele

Wahrscheinlichkeitskalibrierungskurven

Wahrscheinlichkeitskalibrierungskurven

Wahrscheinlichkeitskalibrierung von Klassifikatoren

Wahrscheinlichkeitskalibrierung von Klassifikatoren

Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation

Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation

Klassifikationswahrscheinlichkeit plotten

Klassifikationswahrscheinlichkeit plotten