Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Lasso-Modellauswahl: AIC-BIC / Kreuzvalidierung#
Dieses Beispiel konzentriert sich auf die Modellauswahl für Lasso-Modelle, die lineare Modelle mit L1-Strafe für Regressionsprobleme sind.
Tatsächlich können mehrere Strategien verwendet werden, um den Wert des Regularisierungsparameters auszuwählen: über Kreuzvalidierung oder unter Verwendung eines Informationskriteriums, nämlich AIC oder BIC.
Im Folgenden werden die verschiedenen Strategien im Detail besprochen.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Datensatz#
In diesem Beispiel verwenden wir den Diabetes-Datensatz.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
X.head()
Zusätzlich fügen wir einige zufällige Merkmale zu den ursprünglichen Daten hinzu, um die Merkmalsauswahl durch das Lasso-Modell besser zu veranschaulichen.
import numpy as np
import pandas as pd
rng = np.random.RandomState(42)
n_random_features = 14
X_random = pd.DataFrame(
rng.randn(X.shape[0], n_random_features),
columns=[f"random_{i:02d}" for i in range(n_random_features)],
)
X = pd.concat([X, X_random], axis=1)
# Show only a subset of the columns
X[X.columns[::3]].head()
Lasso-Auswahl über ein Informationskriterium#
LassoLarsIC bietet einen Lasso-Schätzer, der das Akaike Information Criterion (AIC) oder das Bayes Information Criterion (BIC) verwendet, um den optimalen Wert des Regularisierungsparameters alpha auszuwählen.
Vor dem Anpassen des Modells werden die Daten mit einem StandardScaler standardisiert. Darüber hinaus wird die Zeit für das Anpassen und Abstimmen des Hyperparameters alpha gemessen, um sie mit der Kreuzvalidierungsstrategie zu vergleichen.
Wir werden zunächst ein Lasso-Modell mit dem AIC-Kriterium anpassen.
import time
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
start_time = time.time()
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
fit_time = time.time() - start_time
Wir speichern die AIC-Metrik für jeden Wert von alpha, der während fit verwendet wurde.
results = pd.DataFrame(
{
"alphas": lasso_lars_ic[-1].alphas_,
"AIC criterion": lasso_lars_ic[-1].criterion_,
}
).set_index("alphas")
alpha_aic = lasso_lars_ic[-1].alpha_
Nun führen wir die gleiche Analyse unter Verwendung des BIC-Kriteriums durch.
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
results["BIC criterion"] = lasso_lars_ic[-1].criterion_
alpha_bic = lasso_lars_ic[-1].alpha_
Wir können überprüfen, welcher Wert von alpha zum minimalen AIC und BIC führt.
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results.style.apply(highlight_min)
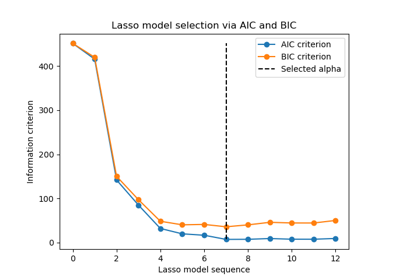
Schließlich können wir die AIC- und BIC-Werte für die verschiedenen alpha-Werte darstellen. Die vertikalen Linien in der Darstellung entsprechen dem für jedes Kriterium ausgewählten alpha. Das ausgewählte alpha entspricht dem Minimum des AIC- oder BIC-Kriteriums.
ax = results.plot()
ax.vlines(
alpha_aic,
results["AIC criterion"].min(),
results["AIC criterion"].max(),
label="alpha: AIC estimate",
linestyles="--",
color="tab:blue",
)
ax.vlines(
alpha_bic,
results["BIC criterion"].min(),
results["BIC criterion"].max(),
label="alpha: BIC estimate",
linestyle="--",
color="tab:orange",
)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel("criterion")
ax.set_xscale("log")
ax.legend()
_ = ax.set_title(
f"Information-criterion for model selection (training time {fit_time:.2f}s)"
)

Die Modellauswahl anhand eines Informationskriteriums ist sehr schnell. Sie basiert auf der Berechnung des Kriteriums auf dem In-Sample-Set, das an fit übergeben wird. Beide Kriterien schätzen den Generalisierungsfehler des Modells basierend auf dem Trainingsset-Fehler und bestrafen diesen übermäßig optimistischen Fehler. Diese Strafe hängt jedoch von einer korrekten Schätzung der Freiheitsgrade und der Rauschvarianz ab. Beide werden für große Stichproben (asymptotische Ergebnisse) abgeleitet und gehen davon aus, dass das Modell korrekt ist, d.h. dass die Daten tatsächlich von diesem Modell generiert werden.
Diese Modelle neigen auch dazu, zusammenzubrechen, wenn das Problem schlecht konditioniert ist (mehr Merkmale als Stichproben). Dann ist es erforderlich, eine Schätzung der Rauschvarianz bereitzustellen.
Lasso-Auswahl über Kreuzvalidierung#
Der Lasso-Schätzer kann mit verschiedenen Lösungsmethoden implementiert werden: Coordinate Descent und Least Angle Regression. Sie unterscheiden sich hinsichtlich ihrer Ausführungsgeschwindigkeit und der Quellen numerischer Fehler.
In scikit-learn stehen zwei verschiedene Schätzer mit integrierter Kreuzvalidierung zur Verfügung: LassoCV und LassoLarsCV, die das Problem jeweils mit Coordinate Descent und Least Angle Regression lösen.
Im Rest dieses Abschnitts werden wir beide Ansätze vorstellen. Für beide Algorithmen verwenden wir eine 20-fache Kreuzvalidierungsstrategie.
Lasso mittels Coordinate Descent#
Beginnen wir mit der Hyperparameter-Abstimmung mithilfe von LassoCV.
from sklearn.linear_model import LassoCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
import matplotlib.pyplot as plt
ymin, ymax = 2300, 3800
lasso = model[-1]
plt.semilogx(lasso.alphas_, lasso.mse_path_, linestyle=":")
plt.plot(
lasso.alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha: CV estimate")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(
f"Mean square error on each fold: coordinate descent (train time: {fit_time:.2f}s)"
)

Lasso mittels Least Angle Regression#
Beginnen wir mit der Hyperparameter-Abstimmung mithilfe von LassoLarsCV.
from sklearn.linear_model import LassoLarsCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoLarsCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
lasso = model[-1]
plt.semilogx(lasso.cv_alphas_, lasso.mse_path_, ":")
plt.semilogx(
lasso.cv_alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha CV")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(f"Mean square error on each fold: Lars (train time: {fit_time:.2f}s)")

Zusammenfassung des Kreuzvalidierungsansatzes#
Beide Algorithmen liefern annähernd die gleichen Ergebnisse.
Lars berechnet einen Lösungspfad nur für jede Biegung im Pfad. Daher ist er sehr effizient, wenn es nur wenige Biegungen gibt, was der Fall ist, wenn es wenige Merkmale oder Stichproben gibt. Außerdem kann er den vollständigen Pfad ohne die Einstellung eines Hyperparameters berechnen. Im Gegensatz dazu berechnet Coordinate Descent die Pfadpunkte auf einem vordefinierten Gitter (hier verwenden wir die Standardeinstellung). Daher ist er effizienter, wenn die Anzahl der Gitterpunkte kleiner ist als die Anzahl der Biegungen im Pfad. Eine solche Strategie kann interessant sein, wenn die Anzahl der Merkmale wirklich groß ist und genügend Stichproben vorhanden sind, um in jede der Kreuzvalidierungs-Falten aufgenommen zu werden. In Bezug auf numerische Fehler wird Lars bei stark korrelierten Variablen mehr Fehler akkumulieren, während der Coordinate-Descent-Algorithmus den Pfad nur auf einem Gitter abtastet.
Beachten Sie, wie der optimale Wert von alpha für jede Falte variiert. Dies veranschaulicht, warum die verschachtelte Kreuzvalidierung eine gute Strategie ist, wenn versucht wird, die Leistung einer Methode zu bewerten, für die ein Parameter mittels Kreuzvalidierung gewählt wird: Diese Wahl des Parameters ist möglicherweise nicht optimal für eine endgültige Bewertung auf einem ausschließlich unbekannten Testdatensatz.
Schlussfolgerung#
In diesem Tutorial wurden zwei Ansätze zur Auswahl des besten Hyperparameters alpha vorgestellt: Eine Strategie findet den optimalen Wert von alpha nur unter Verwendung des Trainingsdatensatzes und eines Informationskriteriums, und eine andere Strategie basiert auf Kreuzvalidierung.
In diesem Beispiel funktionieren beide Ansätze ähnlich. Die In-Sample-Hyperparameter-Auswahl zeigt sogar ihre Effizienz in Bezug auf die Rechenleistung. Sie kann jedoch nur verwendet werden, wenn die Anzahl der Stichproben im Vergleich zur Anzahl der Merkmale ausreichend groß ist.
Deshalb ist die Hyperparameter-Optimierung mittels Kreuzvalidierung eine sichere Strategie: Sie funktioniert in verschiedenen Szenarien.
Gesamtlaufzeit des Skripts: (0 Minuten 0,813 Sekunden)
Verwandte Beispiele