Dimensionsreduktion mit Neighborhood Components Analysis

Beispielanwendung von Neighborhood Components Analysis zur Dimensionsreduktion.

Dieses Beispiel vergleicht verschiedene (lineare) Dimensionsreduktionsmethoden, die auf dem Digits-Datensatz angewendet werden. Der Datensatz enthält Bilder von Ziffern von 0 bis 9 mit ungefähr 180 Stichproben pro Klasse. Jedes Bild hat eine Dimension von 8x8 = 64 und wird auf einen zweidimensionalen Datenpunkt reduziert.

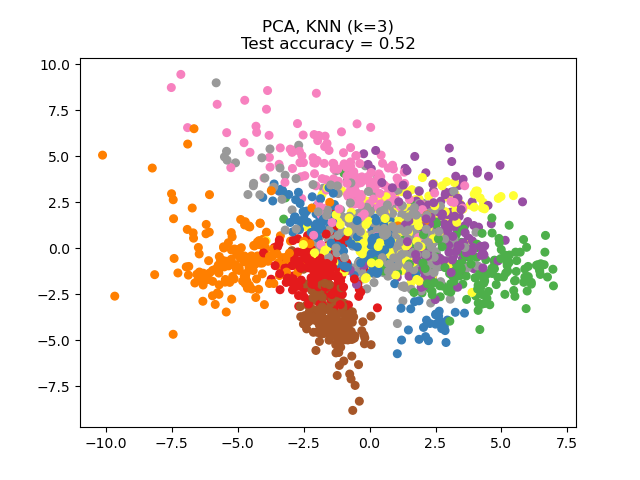
Die auf diesen Datensatz angewendete Hauptkomponentenanalyse (PCA) identifiziert die Kombination von Attributen (Hauptkomponenten oder Richtungen im Merkmalsraum), die die meiste Varianz in den Daten erklären. Hier werden die verschiedenen Stichproben auf den 2 ersten Hauptkomponenten dargestellt.

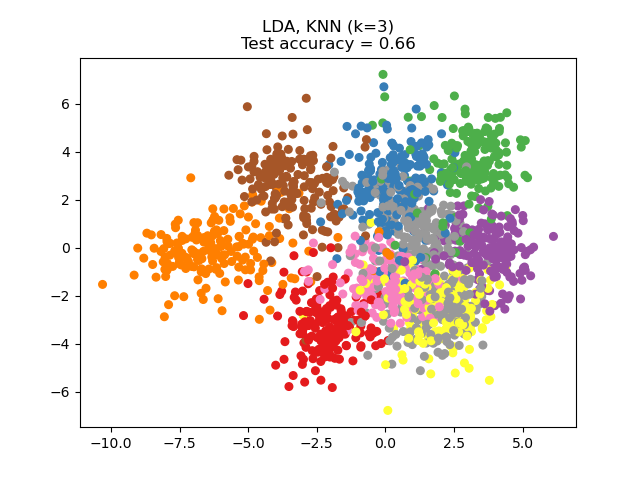
Die Lineare Diskriminanzanalyse (LDA) versucht, Attribute zu identifizieren, die die meiste Varianz *zwischen den Klassen* erklären. Insbesondere ist LDA im Gegensatz zu PCA eine überwachte Methode, die bekannte Klassenbezeichnungen verwendet.

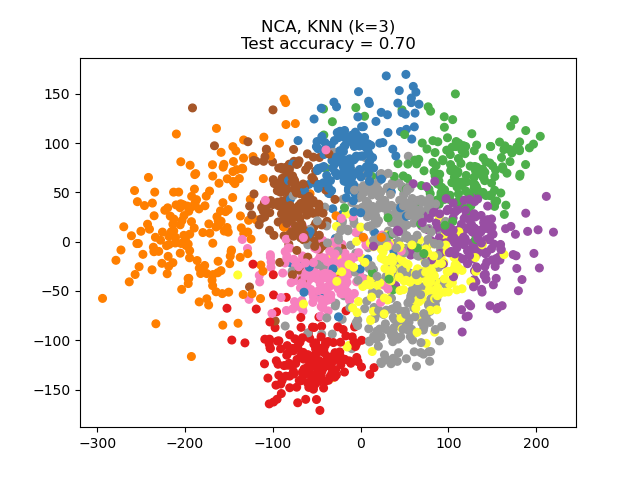
Die Neighborhood Components Analysis (NCA) versucht, einen Merkmalsraum zu finden, mit dem ein stochastischer nächster Nachbar-Algorithmus die beste Genauigkeit erzielt. Wie LDA ist sie eine überwachte Methode.

Man kann sehen, dass NCA eine Gruppierung der Daten erzwingt, die trotz der starken Dimensionsreduktion visuell sinnvoll ist.

• 
• 
• 

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier, NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

n_neighbors = 3
random_state = 0

# Load Digits dataset
X, y = datasets.load_digits(return_X_y=True)

# Split into train/test
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.5, stratify=y, random_state=random_state
)

dim = len(X[0])
n_classes = len(np.unique(y))

# Reduce dimension to 2 with PCA
pca = make_pipeline(StandardScaler(), PCA(n_components=2, random_state=random_state))

# Reduce dimension to 2 with LinearDiscriminantAnalysis
lda = make_pipeline(StandardScaler(), LinearDiscriminantAnalysis(n_components=2))

# Reduce dimension to 2 with NeighborhoodComponentAnalysis
nca = make_pipeline(
    StandardScaler(),
    NeighborhoodComponentsAnalysis(n_components=2, random_state=random_state),
)

# Use a nearest neighbor classifier to evaluate the methods
knn = KNeighborsClassifier(n_neighbors=n_neighbors)

# Make a list of the methods to be compared
dim_reduction_methods = [("PCA", pca), ("LDA", lda), ("NCA", nca)]

# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
    plt.figure()
    # plt.subplot(1, 3, i + 1, aspect=1)

    # Fit the method's model
    model.fit(X_train, y_train)

    # Fit a nearest neighbor classifier on the embedded training set
    knn.fit(model.transform(X_train), y_train)

    # Compute the nearest neighbor accuracy on the embedded test set
    acc_knn = knn.score(model.transform(X_test), y_test)

    # Embed the data set in 2 dimensions using the fitted model
    X_embedded = model.transform(X)

    # Plot the projected points and show the evaluation score
    plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap="Set1")
    plt.title(
        "{}, KNN (k={})\nTest accuracy = {:.2f}".format(name, n_neighbors, acc_knn)
    )
plt.show()

Verwandte Beispiele

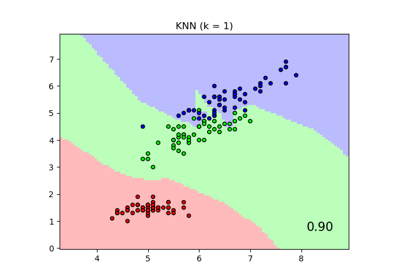
Vergleich von Nächsten Nachbarn mit und ohne Neighborhood Components Analysis

Vergleich von Nächsten Nachbarn mit und ohne Neighborhood Components Analysis

Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

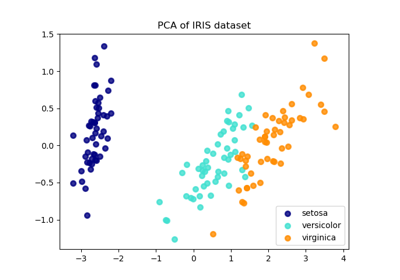
Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

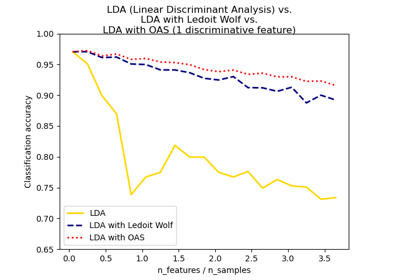
Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Neighborhood Components Analysis Illustration

Neighborhood Components Analysis Illustration