Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
GMM-Initialisierungsmethoden#
Beispiele für die verschiedenen Initialisierungsmethoden in Gaußschen Mischmodellen
Weitere Informationen zum Schätzer finden Sie unter Gaußsche Mischmodelle.
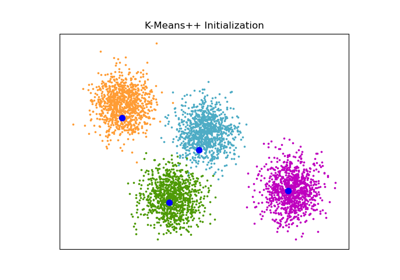
Hier generieren wir einige Beispieldaten mit vier leicht zu identifizierenden Clustern. Der Zweck dieses Beispiels ist die Demonstration der vier verschiedenen Methoden für den Initialisierungsparameter init_param.
Die vier Initialisierungen sind kmeans (Standard), random, random_from_data und k-means++.
Orangefarbene Diamanten stellen die Initialisierungszentren für das durch init_param generierte GMM dar. Die restlichen Daten werden als Kreuze dargestellt und die Farbgebung repräsentiert die endgültige zugeordnete Klassifizierung, nachdem das GMM abgeschlossen ist.
Die Zahlen in der oberen rechten Ecke jedes Unterplots stellen die Anzahl der Iterationen dar, die für die Konvergenz des GaussianMixture benötigt wurden, und die relative Zeit, die für den Initialisierungsteil des Algorithmus benötigt wurde. Kürzere Initialisierungszeiten erfordern tendenziell eine größere Anzahl von Iterationen zur Konvergenz.
Die Initialisierungszeit ist das Verhältnis der für diese Methode benötigten Zeit zur Zeit, die für die Standardmethode kmeans benötigt wurde. Wie Sie sehen können, benötigen alle drei alternativen Methoden weniger Zeit für die Initialisierung im Vergleich zu kmeans.
In diesem Beispiel benötigt das Modell bei Initialisierung mit random_from_data oder random mehr Iterationen zur Konvergenz. Hier leistet k-means++ gute Arbeit, sowohl hinsichtlich der kurzen Initialisierungszeit als auch der geringen Anzahl von Iterationen des GaussianMixture zur Konvergenz.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
from timeit import default_timer as timer
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets._samples_generator import make_blobs
from sklearn.mixture import GaussianMixture
from sklearn.utils.extmath import row_norms
# Generate some data
X, y_true = make_blobs(n_samples=4000, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1]
n_samples = 4000
n_components = 4
x_squared_norms = row_norms(X, squared=True)
def get_initial_means(X, init_params, r):
# Run a GaussianMixture with max_iter=0 to output the initialization means
gmm = GaussianMixture(
n_components=4, init_params=init_params, tol=1e-9, max_iter=0, random_state=r
).fit(X)
return gmm.means_
methods = ["kmeans", "random_from_data", "k-means++", "random"]
colors = ["navy", "turquoise", "cornflowerblue", "darkorange"]
times_init = {}
relative_times = {}
plt.figure(figsize=(4 * len(methods) // 2, 6))
plt.subplots_adjust(
bottom=0.1, top=0.9, hspace=0.15, wspace=0.05, left=0.05, right=0.95
)
for n, method in enumerate(methods):
r = np.random.RandomState(seed=1234)
plt.subplot(2, len(methods) // 2, n + 1)
start = timer()
ini = get_initial_means(X, method, r)
end = timer()
init_time = end - start
gmm = GaussianMixture(
n_components=4, means_init=ini, tol=1e-9, max_iter=2000, random_state=r
).fit(X)
times_init[method] = init_time
for i, color in enumerate(colors):
data = X[gmm.predict(X) == i]
plt.scatter(data[:, 0], data[:, 1], color=color, marker="x")
plt.scatter(
ini[:, 0], ini[:, 1], s=75, marker="D", c="orange", lw=1.5, edgecolors="black"
)
relative_times[method] = times_init[method] / times_init[methods[0]]
plt.xticks(())
plt.yticks(())
plt.title(method, loc="left", fontsize=12)
plt.title(
"Iter %i | Init Time %.2fx" % (gmm.n_iter_, relative_times[method]),
loc="right",
fontsize=10,
)
plt.suptitle("GMM iterations and relative time taken to initialize")
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 0,634 Sekunden)
Verwandte Beispiele
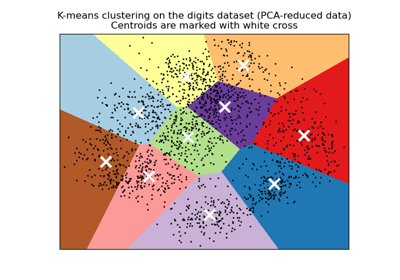
Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten