Sparsere Schätzung der inversen Kovarianz

Verwendung des GraphicalLasso-Schätzers, um eine Kovarianz und eine sparsere Präzision aus einer kleinen Anzahl von Stichproben zu lernen.

Um ein probabilistisches Modell (z.B. ein Gaußsches Modell) zu schätzen, ist die Schätzung der Präzisionsmatrix, d.h. der inversen Kovarianzmatrix, ebenso wichtig wie die Schätzung der Kovarianzmatrix. Tatsächlich wird ein Gaußsches Modell durch die Präzisionsmatrix parametrisiert.

Um günstige Wiederherstellungsbedingungen zu haben, werden die Daten aus einem Modell mit einer sparsen inversen Kovarianzmatrix abgetastet. Zusätzlich stellen wir sicher, dass die Daten nicht zu stark korreliert sind (was den größten Koeffizienten der Präzisionsmatrix begrenzt) und dass keine kleinen Koeffizienten in der Präzisionsmatrix vorhanden sind, die nicht wiederhergestellt werden können. Darüber hinaus ist es bei einer kleinen Anzahl von Beobachtungen einfacher, eine Korrelationsmatrix anstelle einer Kovarianz wiederherzustellen, daher skalieren wir die Zeitreihen.

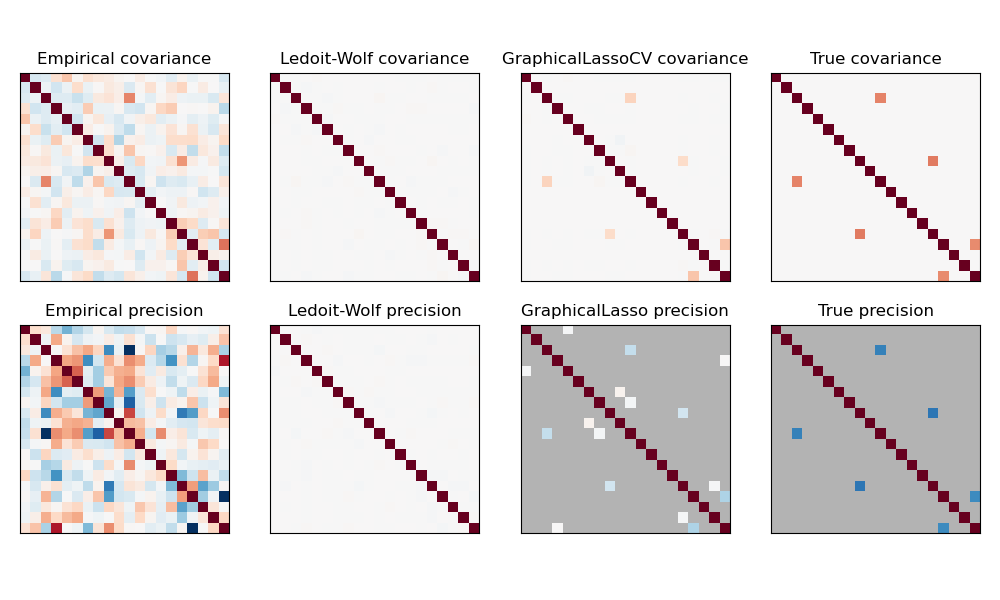
Hier ist die Anzahl der Stichproben etwas größer als die Anzahl der Dimensionen, daher ist die empirische Kovarianz noch invertierbar. Da die Beobachtungen jedoch stark korreliert sind, ist die empirische Kovarianzmatrix schlecht konditioniert und folglich ist ihre Inverse – die empirische Präzisionsmatrix – sehr weit von der Grundwahrheit entfernt.

Wenn wir L2-Shrinkage verwenden, wie beim Ledoit-Wolf-Schätzer, müssen wir, da die Anzahl der Stichproben klein ist, stark schrumpfen. Infolgedessen ist die Ledoit-Wolf-Präzision ziemlich nahe an der tatsächlichen Präzision, die nicht weit davon entfernt ist, diagonal zu sein, aber die Struktur der Nicht-Diagonale geht verloren.

Der L1-penalisierte Schätzer kann einen Teil dieser Nicht-Diagonalstruktur wiederherstellen. Er lernt eine sparsere Präzision. Er ist nicht in der Lage, das exakte Sparsity-Muster wiederherzustellen: Er erkennt zu viele Nicht-Null-Koeffizienten. Die höchsten Nicht-Null-Koeffizienten der L1-Schätzung entsprechen jedoch den Nicht-Null-Koeffizienten in der Grundwahrheit. Schließlich sind die Koeffizienten der L1-Präzisionsschätzung gegen Null verzerrt: Aufgrund der Strafe sind sie alle kleiner als der entsprechende Wert der Grundwahrheit, wie in der Abbildung zu sehen ist.

Beachten Sie, dass der Farbbereich der Präzisionsmatrizen zur besseren Lesbarkeit der Abbildung angepasst wurde. Der gesamte Wertebereich der empirischen Präzision wird nicht angezeigt.

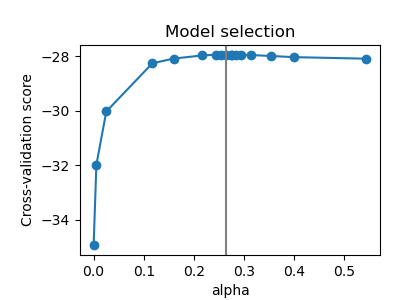
Der Alpha-Parameter von GraphicalLasso, der die Sparsity des Modells festlegt, wird durch interne Kreuzvalidierung in GraphicalLassoCV festgelegt. Wie in Abbildung 2 zu sehen ist, wird das Gitter zur Berechnung des Kreuzvalidierungs-Scores iterativ in der Nähe des Maximums verfeinert.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Generieren Sie die Daten

import numpy as np
from scipy import linalg

from sklearn.datasets import make_sparse_spd_matrix

n_samples = 60
n_features = 20

prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(
    n_features, alpha=0.98, smallest_coef=0.4, largest_coef=0.7, random_state=prng
)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)

Schätzen Sie die Kovarianz

from sklearn.covariance import GraphicalLassoCV, ledoit_wolf

emp_cov = np.dot(X.T, X) / n_samples

model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_

lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)

Ergebnisse plotten

import matplotlib.pyplot as plt

plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)

# plot the covariances
covs = [
    ("Empirical", emp_cov),
    ("Ledoit-Wolf", lw_cov_),
    ("GraphicalLassoCV", cov_),
    ("True", cov),
]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
    plt.subplot(2, 4, i + 1)
    plt.imshow(
        this_cov, interpolation="nearest", vmin=-vmax, vmax=vmax, cmap=plt.cm.RdBu_r
    )
    plt.xticks(())
    plt.yticks(())
    plt.title("%s covariance" % name)


# plot the precisions
precs = [
    ("Empirical", linalg.inv(emp_cov)),
    ("Ledoit-Wolf", lw_prec_),
    ("GraphicalLasso", prec_),
    ("True", prec),
]
vmax = 0.9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
    ax = plt.subplot(2, 4, i + 5)
    plt.imshow(
        np.ma.masked_equal(this_prec, 0),
        interpolation="nearest",
        vmin=-vmax,
        vmax=vmax,
        cmap=plt.cm.RdBu_r,
    )
    plt.xticks(())
    plt.yticks(())
    plt.title("%s precision" % name)
    if hasattr(ax, "set_facecolor"):
        ax.set_facecolor(".7")
    else:
        ax.set_axis_bgcolor(".7")

# plot the model selection metric
plt.figure(figsize=(4, 3))
plt.axes([0.2, 0.15, 0.75, 0.7])
plt.plot(model.cv_results_["alphas"], model.cv_results_["mean_test_score"], "o-")
plt.axvline(model.alpha_, color=".5")
plt.title("Model selection")
plt.ylabel("Cross-validation score")
plt.xlabel("alpha")

plt.show()

Verwandte Beispiele

Präzisions-Rückruf

Präzisions-Rückruf

Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood

Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood

Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid

Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid

Ledoit-Wolf vs OAS Schätzung

Ledoit-Wolf vs OAS Schätzung