Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes

Der Iris-Datensatz repräsentiert 3 Arten von Irisblumen (Setosa, Versicolour und Virginica) mit 4 Attributen: Kelchblattlänge, Kelchblattbreite, Blütenblattlänge und Blütenblattbreite.

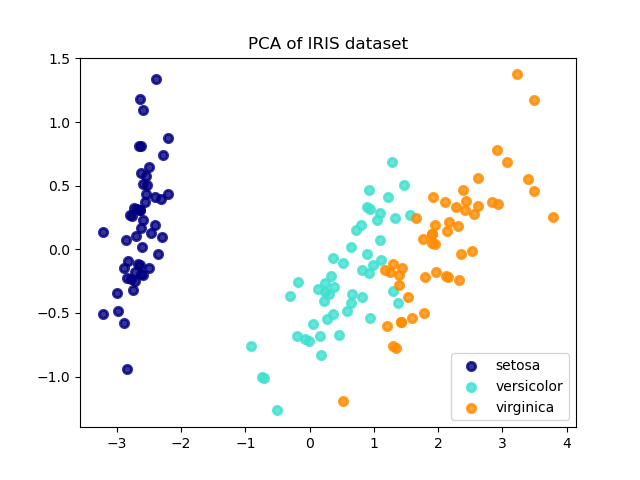
Die Hauptkomponentenanalyse (PCA), die auf diese Daten angewendet wird, identifiziert die Kombination von Attributen (Hauptkomponenten oder Richtungen im Merkmalsraum), die die meiste Varianz in den Daten erklären. Hier werden die verschiedenen Stichproben auf den 2 ersten Hauptkomponenten dargestellt.

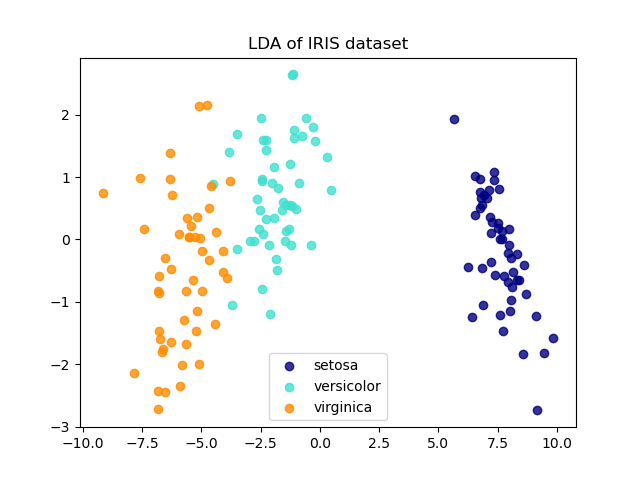
Die Lineare Diskriminanzanalyse (LDA) versucht, Attribute zu identifizieren, die die meiste Varianz zwischen den Klassen erklären. Insbesondere ist LDA im Gegensatz zur PCA eine überwachte Methode, die bekannte Klassenbezeichnungen verwendet.

• 
• 

explained variance ratio (first two components): [0.92461872 0.05306648]

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)

lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)

# Percentage of variance explained for each components
print(
    "explained variance ratio (first two components): %s"
    % str(pca.explained_variance_ratio_)
)

plt.figure()
colors = ["navy", "turquoise", "darkorange"]
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(
        X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=0.8, lw=lw, label=target_name
    )
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("PCA of IRIS dataset")

plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(
        X_r2[y == i, 0], X_r2[y == i, 1], alpha=0.8, color=color, label=target_name
    )
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("LDA of IRIS dataset")

plt.show()

Verwandte Beispiele

Principal Component Analysis (PCA) auf dem Iris-Datensatz

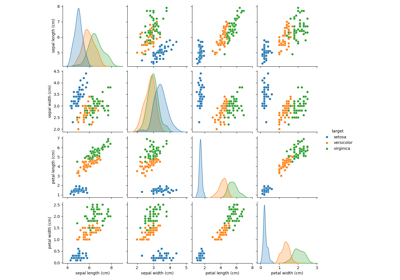
Principal Component Analysis (PCA) auf dem Iris-Datensatz

Dimensionsreduktion mit Neighborhood Components Analysis

Dimensionsreduktion mit Neighborhood Components Analysis

Inkrementelles PCA

Inkrementelles PCA

Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten

Entscheidungsfläche von Entscheidungsbäumen, trainiert auf dem Iris-Datensatz, plotten