Hinweis
Gehe zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Auswertung von Ausreißererkennungs-Schätzern#
Dieses Beispiel vergleicht zwei Algorithmen zur Ausreißererkennung, nämlich Local Outlier Factor (LOF) und Isolation Forest (IForest), auf realen Datensätzen, die in sklearn.datasets verfügbar sind. Ziel ist es zu zeigen, dass verschiedene Algorithmen auf verschiedenen Datensätzen gut funktionieren und ihre Trainingsgeschwindigkeit und Empfindlichkeit gegenüber Hyperparametern zu kontrastieren.
Die Algorithmen werden (ohne Labels) auf dem gesamten Datensatz trainiert, von dem angenommen wird, dass er Ausreißer enthält.
Die ROC-Kurven werden mithilfe des Wissens über die Ground-Truth-Labels berechnet und mithilfe von
RocCurveDisplayangezeigt.Die Leistung wird in Bezug auf den ROC-AUC bewertet.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Datenvorverarbeitung und Modelltraining#
Verschiedene Modelle zur Ausreißererkennung erfordern eine unterschiedliche Vorverarbeitung. Bei kategorialen Variablen ist OrdinalEncoder oft eine gute Strategie für baumbasierte Modelle wie IsolationForest, während nachbarschaftsbasierte Modelle wie LocalOutlierFactor durch die durch die ordinale Kodierung induzierte Reihenfolge beeinflusst würden. Um eine Reihenfolge zu vermeiden, sollte stattdessen OneHotEncoder verwendet werden.
Nachbarschaftsbasierte Modelle können auch eine Skalierung der numerischen Merkmale erfordern (siehe z. B. Auswirkung der Skalierung auf ein k-Nachbarschaftsmodell). In Anwesenheit von Ausreißern ist eine gute Option die Verwendung eines RobustScaler.
from sklearn.compose import ColumnTransformer
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
OneHotEncoder,
OrdinalEncoder,
RobustScaler,
)
def make_estimator(name, categorical_columns=None, iforest_kw=None, lof_kw=None):
"""Create an outlier detection estimator based on its name."""
if name == "LOF":
outlier_detector = LocalOutlierFactor(**(lof_kw or {}))
if categorical_columns is None:
preprocessor = RobustScaler()
else:
preprocessor = ColumnTransformer(
transformers=[("categorical", OneHotEncoder(), categorical_columns)],
remainder=RobustScaler(),
)
else: # name == "IForest"
outlier_detector = IsolationForest(**(iforest_kw or {}))
if categorical_columns is None:
preprocessor = None
else:
ordinal_encoder = OrdinalEncoder(
handle_unknown="use_encoded_value", unknown_value=-1
)
preprocessor = ColumnTransformer(
transformers=[
("categorical", ordinal_encoder, categorical_columns),
],
remainder="passthrough",
)
return make_pipeline(preprocessor, outlier_detector)
Die folgende Funktion fit_predict gibt den durchschnittlichen Ausreißer-Score von X zurück.
from time import perf_counter
def fit_predict(estimator, X):
tic = perf_counter()
if estimator[-1].__class__.__name__ == "LocalOutlierFactor":
estimator.fit(X)
y_score = estimator[-1].negative_outlier_factor_
else: # "IsolationForest"
y_score = estimator.fit(X).decision_function(X)
toc = perf_counter()
print(f"Duration for {model_name}: {toc - tic:.2f} s")
return y_score
Im Rest des Beispiels verarbeiten wir einen Datensatz pro Abschnitt. Nach dem Laden der Daten werden die Zielwerte so modifiziert, dass sie aus zwei Klassen bestehen: 0 steht für Inlier und 1 für Ausreißer. Aufgrund von Rechenbeschränkungen der Dokumentation von scikit-learn wird die Stichprobengröße einiger Datensätze mithilfe eines stratifizierten train_test_split reduziert.
Darüber hinaus setzen wir n_neighbors so, dass er der erwarteten Anzahl von Anomalien entspricht: expected_n_anomalies = n_samples * expected_anomaly_fraction. Dies ist eine gute Heuristik, solange der Anteil der Ausreißer nicht sehr gering ist, da n_neighbors mindestens größer als die Anzahl der Samples im schwächer besiedelten Cluster sein sollte (siehe Ausreißererkennung mit Local Outlier Factor (LOF)).
KDDCup99 - SA-Datensatz#
Der Kddcup 99 Datensatz wurde mit einem geschlossenen Netzwerk und manuell eingefügten Angriffen generiert. Der SA-Datensatz ist eine Teilmenge davon, die durch einfaches Auswählen aller normalen Daten und einem Anomalieanteil von etwa 3 % erhalten wurde.
import numpy as np
from sklearn.datasets import fetch_kddcup99
from sklearn.model_selection import train_test_split
X, y = fetch_kddcup99(
subset="SA", percent10=True, random_state=42, return_X_y=True, as_frame=True
)
y = (y != b"normal.").astype(np.int32)
X, _, y, _ = train_test_split(X, y, train_size=0.1, stratify=y, random_state=42)
n_samples, anomaly_frac = X.shape[0], y.mean()
print(f"{n_samples} datapoints with {y.sum()} anomalies ({anomaly_frac:.02%})")
10065 datapoints with 338 anomalies (3.36%)
Der SA-Datensatz enthält 41 Merkmale, von denen 3 kategorial sind: „protocol_type“, „service“ und „flag“.
y_true = {}
y_score = {"LOF": {}, "IForest": {}}
model_names = ["LOF", "IForest"]
cat_columns = ["protocol_type", "service", "flag"]
y_true["KDDCup99 - SA"] = y
for model_name in model_names:
model = make_estimator(
name=model_name,
categorical_columns=cat_columns,
lof_kw={"n_neighbors": int(n_samples * anomaly_frac)},
iforest_kw={"random_state": 42},
)
y_score[model_name]["KDDCup99 - SA"] = fit_predict(model, X)
Duration for LOF: 2.15 s
Duration for IForest: 0.27 s
Forest Covertypes-Datensatz#
Die Forest Covertypes sind ein Multiklassen-Datensatz, bei dem das Ziel die dominante Baumart in einem Waldgebiet ist. Er enthält 54 Merkmale, von denen einige („Wilderness_Area“ und „Soil_Type“) bereits binär kodiert sind. Obwohl ursprünglich als Klassifizierungsaufgabe gedacht, kann man Inlier als Samples mit dem Label 2 und Ausreißer als Samples mit dem Label 4 betrachten.
from sklearn.datasets import fetch_covtype
X, y = fetch_covtype(return_X_y=True, as_frame=True)
s = (y == 2) + (y == 4)
X = X.loc[s]
y = y.loc[s]
y = (y != 2).astype(np.int32)
X, _, y, _ = train_test_split(X, y, train_size=0.05, stratify=y, random_state=42)
X_forestcover = X # save X for later use
n_samples, anomaly_frac = X.shape[0], y.mean()
print(f"{n_samples} datapoints with {y.sum()} anomalies ({anomaly_frac:.02%})")
14302 datapoints with 137 anomalies (0.96%)
y_true["forestcover"] = y
for model_name in model_names:
model = make_estimator(
name=model_name,
lof_kw={"n_neighbors": int(n_samples * anomaly_frac)},
iforest_kw={"random_state": 42},
)
y_score[model_name]["forestcover"] = fit_predict(model, X)
Duration for LOF: 1.96 s
Duration for IForest: 0.22 s
Ames Housing-Datensatz#
Der Ames Housing Datensatz ist ursprünglich ein Regressionsdatensatz, bei dem das Ziel die Verkaufspreise von Häusern in Ames, Iowa, sind. Hier wandeln wir ihn in ein Ausreißererkennungsproblem um, indem wir Häuser mit einem Preis über 70 USD/Quadratfuß betrachten. Um das Problem zu vereinfachen, lassen wir die Zwischenpreise zwischen 40 und 70 USD/Quadratfuß weg.
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
X, y = fetch_openml(name="ames_housing", version=1, return_X_y=True, as_frame=True)
y = y.div(X["Lot_Area"])
# None values in pandas 1.5.1 were mapped to np.nan in pandas 2.0.1
X["Misc_Feature"] = X["Misc_Feature"].cat.add_categories("NoInfo").fillna("NoInfo")
X["Mas_Vnr_Type"] = X["Mas_Vnr_Type"].cat.add_categories("NoInfo").fillna("NoInfo")
X.drop(columns="Lot_Area", inplace=True)
mask = (y < 40) | (y > 70)
X = X.loc[mask]
y = y.loc[mask]
y.hist(bins=20, edgecolor="black")
plt.xlabel("House price in USD/sqft")
_ = plt.title("Distribution of house prices in Ames")
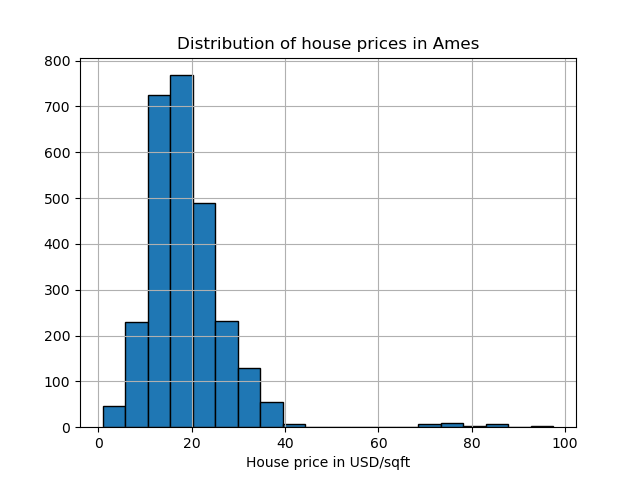
y = (y > 70).astype(np.int32)
n_samples, anomaly_frac = X.shape[0], y.mean()
print(f"{n_samples} datapoints with {y.sum()} anomalies ({anomaly_frac:.02%})")
2714 datapoints with 30 anomalies (1.11%)
Der Datensatz enthält 46 kategoriale Merkmale. In diesem Fall ist es einfacher, einen make_column_selector zu verwenden, um diese zu finden, anstatt eine handerstellte Liste zu übergeben.
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include="category")
cat_columns = categorical_columns_selector(X)
y_true["ames_housing"] = y
for model_name in model_names:
model = make_estimator(
name=model_name,
categorical_columns=cat_columns,
lof_kw={"n_neighbors": int(n_samples * anomaly_frac)},
iforest_kw={"random_state": 42},
)
y_score[model_name]["ames_housing"] = fit_predict(model, X)
Duration for LOF: 0.85 s
Duration for IForest: 0.21 s
Cardiotocography-Datensatz#
Der Cardiotocography Datensatz ist ein Multiklassen-Datensatz von fetalen Kardiotokogrammen, wobei die Klassen das fetale Herzfrequenzmuster (FHR) sind, das mit Labels von 1 bis 10 kodiert ist. Hier setzen wir Klasse 3 (die Minderheitsklasse) als Ausreißer. Er enthält 30 numerische Merkmale, von denen einige binär kodiert und einige kontinuierlich sind.
X, y = fetch_openml(name="cardiotocography", version=1, return_X_y=True, as_frame=False)
X_cardiotocography = X # save X for later use
s = y == "3"
y = s.astype(np.int32)
n_samples, anomaly_frac = X.shape[0], y.mean()
print(f"{n_samples} datapoints with {y.sum()} anomalies ({anomaly_frac:.02%})")
2126 datapoints with 53 anomalies (2.49%)
y_true["cardiotocography"] = y
for model_name in model_names:
model = make_estimator(
name=model_name,
lof_kw={"n_neighbors": int(n_samples * anomaly_frac)},
iforest_kw={"random_state": 42},
)
y_score[model_name]["cardiotocography"] = fit_predict(model, X)
Duration for LOF: 0.06 s
Duration for IForest: 0.14 s
Ergebnisse plotten und interpretieren#
Die Leistung des Algorithmus bezieht sich darauf, wie gut die Rate der wahren positiven Fälle (TPR) bei geringen Werten der Rate der falsch positiven Fälle (FPR) ist. Die besten Algorithmen haben die Kurve oben links im Diagramm und die Fläche unter der Kurve (AUC) nahe 1. Die diagonale gestrichelte Linie repräsentiert eine zufällige Klassifizierung von Ausreißern und Inliern.
import math
from sklearn.metrics import RocCurveDisplay
cols = 2
pos_label = 0 # mean 0 belongs to positive class
datasets_names = y_true.keys()
rows = math.ceil(len(datasets_names) / cols)
fig, axs = plt.subplots(nrows=rows, ncols=cols, squeeze=False, figsize=(10, rows * 4))
for ax, dataset_name in zip(axs.ravel(), datasets_names):
for model_idx, model_name in enumerate(model_names):
display = RocCurveDisplay.from_predictions(
y_true[dataset_name],
y_score[model_name][dataset_name],
pos_label=pos_label,
name=model_name,
ax=ax,
plot_chance_level=(model_idx == len(model_names) - 1),
chance_level_kw={"linestyle": ":"},
)
ax.set_title(dataset_name)
_ = plt.tight_layout(pad=2.0) # spacing between subplots
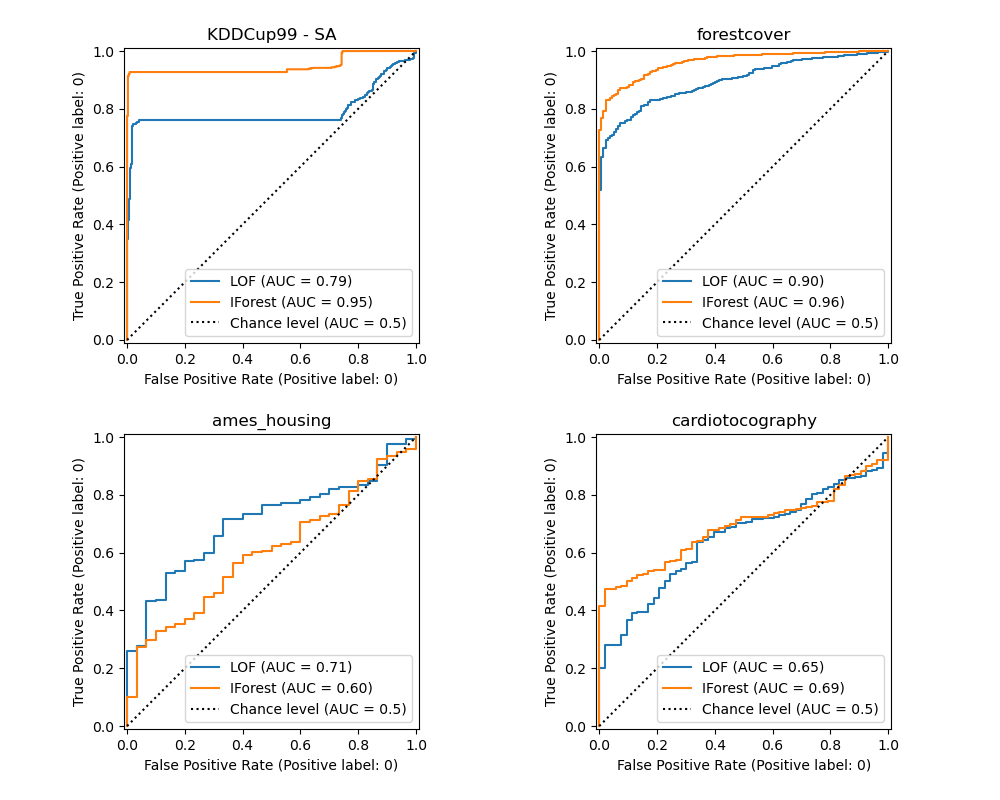
Wir beobachten, dass LOF und IForest, sobald die Anzahl der Nachbarn optimiert ist, in Bezug auf den ROC-AUC für die Datensätze Forestcover und Cardiotocography ähnlich gut abschneiden. Der Score für IForest ist für den SA-Datensatz geringfügig besser und LOF schneidet auf dem Ames Housing Datensatz deutlich besser ab als IForest.
Beachten Sie jedoch, dass Isolation Forest auf Datensätzen mit einer großen Anzahl von Samples tendenziell viel schneller trainiert als LOF. LOF muss paarweise Distanzen berechnen, um die nächsten Nachbarn zu finden, was eine quadratische Komplexität in Bezug auf die Anzahl der Beobachtungen hat. Dies kann diese Methode auf großen Datensätzen unerschwinglich machen.
Ablationsstudie#
In diesem Abschnitt untersuchen wir den Einfluss des Hyperparameters n_neighbors und der Wahl der Skalierung der numerischen Variablen auf das LOF-Modell. Hier verwenden wir den Forest Covertypes-Datensatz, da die binär kodierten Kategorien eine natürliche Skala für euklidische Distanzen zwischen 0 und 1 einführen. Wir möchten dann eine Skalierungsmethode verwenden, um zu vermeiden, dass nicht-binären Merkmalen ein Vorrang eingeräumt wird, und die robust genug gegen Ausreißer ist, damit die Aufgabe, diese zu finden, nicht zu schwierig wird.
X = X_forestcover
y = y_true["forestcover"]
n_samples = X.shape[0]
n_neighbors_list = (n_samples * np.array([0.2, 0.02, 0.01, 0.001])).astype(np.int32)
model = make_pipeline(RobustScaler(), LocalOutlierFactor())
linestyles = ["solid", "dashed", "dashdot", ":", (5, (10, 3))]
fig, ax = plt.subplots()
for model_idx, (linestyle, n_neighbors) in enumerate(zip(linestyles, n_neighbors_list)):
model.set_params(localoutlierfactor__n_neighbors=n_neighbors)
model.fit(X)
y_score = model[-1].negative_outlier_factor_
display = RocCurveDisplay.from_predictions(
y,
y_score,
pos_label=pos_label,
name=f"n_neighbors = {n_neighbors}",
ax=ax,
plot_chance_level=(model_idx == len(n_neighbors_list) - 1),
chance_level_kw={"linestyle": (0, (1, 10))},
curve_kwargs=dict(linestyle=linestyle, linewidth=2),
)
_ = ax.set_title("RobustScaler with varying n_neighbors\non forestcover dataset")
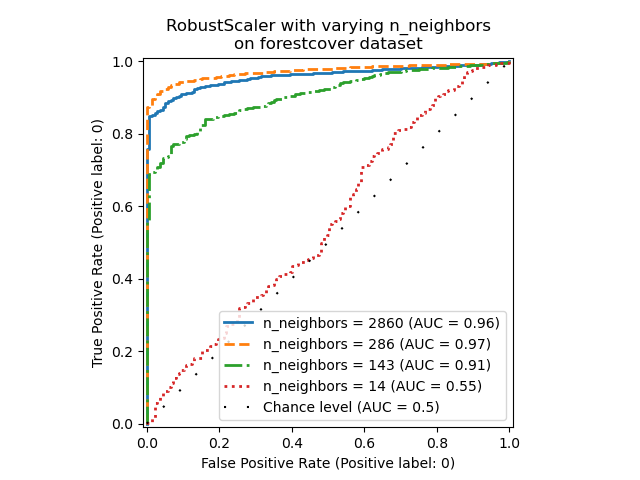
Wir beobachten, dass die Anzahl der Nachbarn einen großen Einfluss auf die Leistung des Modells hat. Wenn man Zugriff auf (zumindest einige) Ground-Truth-Labels hat, ist es wichtig, n_neighbors entsprechend zu optimieren. Eine bequeme Möglichkeit, dies zu tun, ist die Untersuchung von Werten für n_neighbors, die in der Größenordnung der erwarteten Kontamination liegen.
from sklearn.preprocessing import MinMaxScaler, SplineTransformer, StandardScaler
preprocessor_list = [
None,
RobustScaler(),
StandardScaler(),
MinMaxScaler(),
SplineTransformer(),
]
expected_anomaly_fraction = 0.02
lof = LocalOutlierFactor(n_neighbors=int(n_samples * expected_anomaly_fraction))
fig, ax = plt.subplots()
for model_idx, (linestyle, preprocessor) in enumerate(
zip(linestyles, preprocessor_list)
):
model = make_pipeline(preprocessor, lof)
model.fit(X)
y_score = model[-1].negative_outlier_factor_
display = RocCurveDisplay.from_predictions(
y,
y_score,
pos_label=pos_label,
name=str(preprocessor).split("(")[0],
ax=ax,
plot_chance_level=(model_idx == len(preprocessor_list) - 1),
chance_level_kw={"linestyle": (0, (1, 10))},
curve_kwargs=dict(linestyle=linestyle, linewidth=2),
)
_ = ax.set_title("Fixed n_neighbors with varying preprocessing\non forestcover dataset")
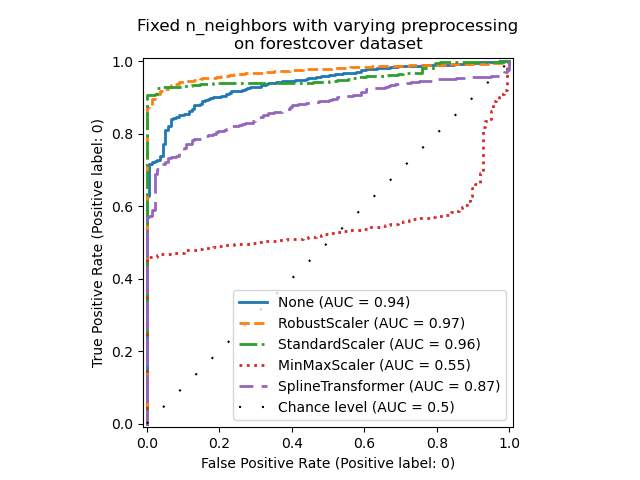
Einerseits skaliert RobustScaler jedes Merkmal unabhängig, indem standardmäßig der Interquartilsabstand (IQR) verwendet wird, der den Bereich zwischen dem 25. und 75. Perzentil der Daten darstellt. Er zentriert die Daten, indem der Median abgezogen wird, und skaliert sie dann durch Division durch den IQR. Der IQR ist robust gegenüber Ausreißern: Der Median und der Interquartilsabstand werden von extremen Werten weniger beeinflusst als der Bereich, der Mittelwert und die Standardabweichung. Darüber hinaus quetscht RobustScaler marginale Ausreißerwerte nicht, im Gegensatz zu StandardScaler.
Andererseits skaliert MinMaxScaler jedes Merkmal einzeln so, dass sein Bereich in den Bereich zwischen Null und Eins abgebildet wird. Wenn Ausreißer in den Daten vorhanden sind, können sie diese zu den minimalen oder maximalen Werten hin verschieben, was zu einer völlig anderen Verteilung der Daten mit großen marginalen Ausreißern führt: Alle Nicht-Ausreißerwerte können dadurch fast zusammenfallen.
Wir haben auch keine Vorverarbeitung (durch Übergabe von None an die Pipeline), StandardScaler und SplineTransformer ausgewertet. Bitte beachten Sie deren jeweilige Dokumentation für weitere Details.
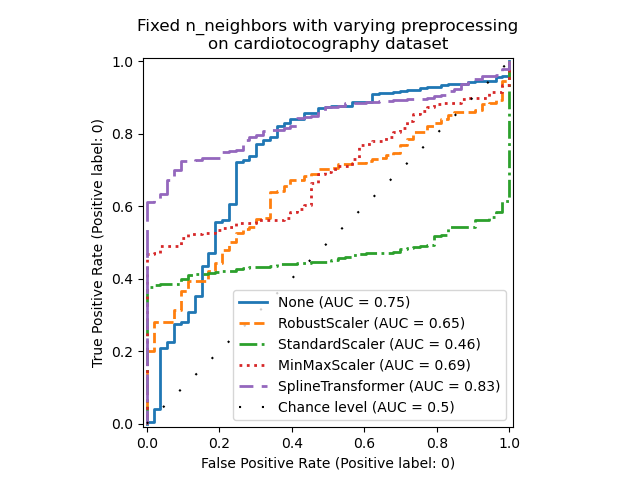
Beachten Sie, dass die optimale Vorverarbeitung vom Datensatz abhängt, wie unten gezeigt
X = X_cardiotocography
y = y_true["cardiotocography"]
n_samples, expected_anomaly_fraction = X.shape[0], 0.025
lof = LocalOutlierFactor(n_neighbors=int(n_samples * expected_anomaly_fraction))
fig, ax = plt.subplots()
for model_idx, (linestyle, preprocessor) in enumerate(
zip(linestyles, preprocessor_list)
):
model = make_pipeline(preprocessor, lof)
model.fit(X)
y_score = model[-1].negative_outlier_factor_
display = RocCurveDisplay.from_predictions(
y,
y_score,
pos_label=pos_label,
name=str(preprocessor).split("(")[0],
ax=ax,
plot_chance_level=(model_idx == len(preprocessor_list) - 1),
chance_level_kw={"linestyle": (0, (1, 10))},
curve_kwargs=dict(linestyle=linestyle, linewidth=2),
)
ax.set_title(
"Fixed n_neighbors with varying preprocessing\non cardiotocography dataset"
)
plt.show()
Gesamte Laufzeit des Skripts: (1 Minuten 5.097 Sekunden)
Verwandte Beispiele
Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen

Vergleich der Auswirkungen verschiedener Skalierer auf Daten mit Ausreißern

Neuartigkeitserkennung mit Local Outlier Factor (LOF)