Kurvenanpassung mit Bayes'scher Ridge-Regression

Berechnet eine Bayes'sche Ridge-Regression von Sinusoiden.

Weitere Informationen zur Regressionsmethode finden Sie unter Bayes'sche Ridge-Regression.

Im Allgemeinen kann bei der Anpassung einer Kurve mit einem Polynom durch Bayes'sche Ridge-Regression die Auswahl der Anfangswerte der Regularisierungsparameter (alpha, lambda) wichtig sein. Dies liegt daran, dass die Regularisierungsparameter durch ein iteratives Verfahren bestimmt werden, das von den Anfangswerten abhängt.

In diesem Beispiel wird die Sinusoide mithilfe verschiedener Paare von Anfangswerten durch ein Polynom approximiert.

Wenn man von den Standardwerten (alpha_init = 1.90, lambda_init = 1.) ausgeht, ist der Bias der resultierenden Kurve groß und die Varianz klein. Daher sollte lambda_init relativ klein (1.e-3) sein, um den Bias zu reduzieren.

Durch die Auswertung der logarithmischen marginalen Likelihood (L) dieser Modelle können wir auch bestimmen, welches besser ist. Es kann daraus geschlossen werden, dass das Modell mit größerem L wahrscheinlicher ist.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Generieren von Sinusoid-Daten mit Rauschen

import numpy as np


def func(x):
    return np.sin(2 * np.pi * x)


size = 25
rng = np.random.RandomState(1234)
x_train = rng.uniform(0.0, 1.0, size)
y_train = func(x_train) + rng.normal(scale=0.1, size=size)
x_test = np.linspace(0.0, 1.0, 100)

Anpassung durch kubisches Polynom

from sklearn.linear_model import BayesianRidge

n_order = 3
X_train = np.vander(x_train, n_order + 1, increasing=True)
X_test = np.vander(x_test, n_order + 1, increasing=True)
reg = BayesianRidge(tol=1e-6, fit_intercept=False, compute_score=True)

Plot der wahren und vorhergesagten Kurven mit logarithmischer marginaler Likelihood (L)

import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for i, ax in enumerate(axes):
    # Bayesian ridge regression with different initial value pairs
    if i == 0:
        init = [1 / np.var(y_train), 1.0]  # Default values
    elif i == 1:
        init = [1.0, 1e-3]
        reg.set_params(alpha_init=init[0], lambda_init=init[1])
    reg.fit(X_train, y_train)
    ymean, ystd = reg.predict(X_test, return_std=True)

    ax.plot(x_test, func(x_test), color="blue", label="sin($2\\pi x$)")
    ax.scatter(x_train, y_train, s=50, alpha=0.5, label="observation")
    ax.plot(x_test, ymean, color="red", label="predict mean")
    ax.fill_between(
        x_test, ymean - ystd, ymean + ystd, color="pink", alpha=0.5, label="predict std"
    )
    ax.set_ylim(-1.3, 1.3)
    ax.legend()
    title = "$\\alpha$_init$={:.2f},\\ \\lambda$_init$={}$".format(init[0], init[1])
    if i == 0:
        title += " (Default)"
    ax.set_title(title, fontsize=12)
    text = "$\\alpha={:.1f}$\n$\\lambda={:.3f}$\n$L={:.1f}$".format(
        reg.alpha_, reg.lambda_, reg.scores_[-1]
    )
    ax.text(0.05, -1.0, text, fontsize=12)

plt.tight_layout()
plt.show()

Verwandte Beispiele

Vergleich von linearen Bayes'schen Regressoren

Vergleich von linearen Bayes'schen Regressoren

Verwendung von KBinsDiscretizer zur Diskretisierung kontinuierlicher Merkmale

Verwendung von KBinsDiscretizer zur Diskretisierung kontinuierlicher Merkmale

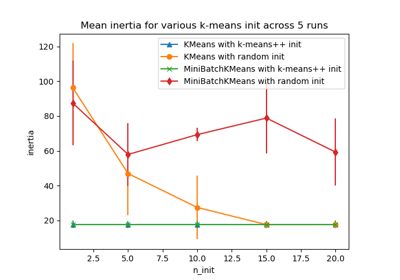
Empirische Auswertung des Einflusses der K-Means Initialisierung

Empirische Auswertung des Einflusses der K-Means Initialisierung

Gradient Boosting Regression

Gradient Boosting Regression