Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Verzögerte Merkmale für Zeitreihenprognosen#
Dieses Beispiel zeigt, wie durch Polars erstellte verzögerte Merkmale für die Zeitreihenprognose mit HistGradientBoostingRegressor auf dem Bike Sharing Demand Datensatz verwendet werden können.
Sehen Sie sich das Beispiel für Zeitbezogene Merkmalserstellung an, um einige Datenexplorationen zu diesem Datensatz und eine Demonstration der periodischen Merkmalserstellung zu erhalten.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Analyse des Bike Sharing Demand Datensatzes#
Wir beginnen mit dem Laden der Daten aus dem OpenML Repository als Roh-Parquet-Datei, um zu veranschaulichen, wie mit einer beliebigen Parquet-Datei gearbeitet wird, anstatt diesen Schritt in einem Komfort-Tool wie sklearn.datasets.fetch_openml zu verbergen.
Die URL der Parquet-Datei finden Sie in der JSON-Beschreibung des Bike Sharing Demand Datensatzes mit der ID 44063 auf openml.org (https://openml.org/search?type=data&status=active&id=44063).
Der sha256-Hash der Datei wird ebenfalls bereitgestellt, um die Integrität der heruntergeladenen Datei sicherzustellen.
import numpy as np
import polars as pl
from sklearn.datasets import fetch_file
pl.Config.set_fmt_str_lengths(20)
bike_sharing_data_file = fetch_file(
"https://data.openml.org/datasets/0004/44063/dataset_44063.pq",
sha256="d120af76829af0d256338dc6dd4be5df4fd1f35bf3a283cab66a51c1c6abd06a",
)
bike_sharing_data_file
PosixPath('/home/circleci/scikit_learn_data/data.openml.org/datasets_0004_44063/dataset_44063.pq')
Wir laden die Parquet-Datei mit Polars für die Merkmalserstellung. Polars speichert gängige Teilausdrücke, die in mehreren Ausdrücken wiederverwendet werden (wie pl.col("count").shift(1) unten), automatisch im Cache. Weitere Informationen finden Sie unter https://docs.pola.rs/user-guide/lazy/optimizations/.
df = pl.read_parquet(bike_sharing_data_file)
Als Nächstes betrachten wir die statistische Zusammenfassung des Datensatzes, um die Daten, mit denen wir arbeiten, besser zu verstehen.
import polars.selectors as cs
summary = df.select(cs.numeric()).describe()
summary
Betrachten wir die Anzahl der Jahreszeiten "fall", "spring", "summer" und "winter" im Datensatz, um zu bestätigen, dass sie ausgewogen sind.
import matplotlib.pyplot as plt
df["season"].value_counts()
Generierung von durch Polars erstellten verzögerten Merkmalen#
Betrachten wir das Problem, die Nachfrage in der nächsten Stunde anhand vergangener Nachfragedaten vorherzusagen. Da die Nachfrage eine kontinuierliche Variable ist, könnte man intuitiv jedes Regressionsmodell verwenden. Wir haben jedoch nicht den üblichen (X_train, y_train)-Datensatz. Stattdessen haben wir nur die y_train-Nachfragedaten, die sequenziell nach Zeit geordnet sind.
lagged_df = df.select(
"count",
*[pl.col("count").shift(i).alias(f"lagged_count_{i}h") for i in [1, 2, 3]],
lagged_count_1d=pl.col("count").shift(24),
lagged_count_1d_1h=pl.col("count").shift(24 + 1),
lagged_count_7d=pl.col("count").shift(7 * 24),
lagged_count_7d_1h=pl.col("count").shift(7 * 24 + 1),
lagged_mean_24h=pl.col("count").shift(1).rolling_mean(24),
lagged_max_24h=pl.col("count").shift(1).rolling_max(24),
lagged_min_24h=pl.col("count").shift(1).rolling_min(24),
lagged_mean_7d=pl.col("count").shift(1).rolling_mean(7 * 24),
lagged_max_7d=pl.col("count").shift(1).rolling_max(7 * 24),
lagged_min_7d=pl.col("count").shift(1).rolling_min(7 * 24),
)
lagged_df.tail(10)
Vorsicht jedoch, die ersten Zeilen haben undefinierte Werte, da ihre eigene Vergangenheit unbekannt ist. Dies hängt davon ab, wie viel Verzögerung wir verwendet haben.
lagged_df.head(10)
Wir können nun die verzögerten Merkmale in einer Matrix X und die Zielvariable (die zu prognostizierenden Anzahlen) in einem Array mit der gleichen ersten Dimension y trennen.
lagged_df = lagged_df.drop_nulls()
X = lagged_df.drop("count")
y = lagged_df["count"]
print("X shape: {}\ny shape: {}".format(X.shape, y.shape))
X shape: (17210, 13)
y shape: (17210,)
Naive Bewertung der Regression der Fahrradnachfrage der nächsten Stunde#
Lassen Sie uns unseren tabellarisierten Datensatz zufällig aufteilen, um ein Gradient Boosting Regression Tree (GBRT)-Modell zu trainieren und es mit dem Mean Absolute Percentage Error (MAPE) zu bewerten. Wenn unser Modell auf Prognose abzielt (d.h. zukünftige Daten aus vergangenen Daten vorhersagt), sollten wir keine Trainingsdaten verwenden, die jünger sind als die Testdaten. Im Zeitreihen-Machine-Learning gilt die "i.i.d." (unabhängig und identisch verteilt) Annahme nicht, da die Datenpunkte nicht unabhängig sind und eine zeitliche Beziehung aufweisen.
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
model = HistGradientBoostingRegressor().fit(X_train, y_train)
Betrachten wir die Leistung des Modells.
from sklearn.metrics import mean_absolute_percentage_error
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.3889873516666431
Korrekte Bewertung der Prognose der nächsten Stunde#
Verwenden wir geeignete Bewertungsstrategien, die die zeitliche Struktur des Datensatzes berücksichtigen, um die Fähigkeit unseres Modells zur Vorhersage von Datenpunkten in der Zukunft zu bewerten (um Betrug durch das Lesen von Werten aus den verzögerten Merkmalen im Trainingssatz zu vermeiden).
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=3, # to keep the notebook fast enough on common laptops
gap=48, # 2 days data gap between train and test
max_train_size=10000, # keep train sets of comparable sizes
test_size=3000, # for 2 or 3 digits of precision in scores
)
all_splits = list(ts_cv.split(X, y))
Training des Modells und Bewertung seiner Leistung anhand von MAPE.
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
model = HistGradientBoostingRegressor().fit(X_train, y_train)
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.44300751539296973
Der Generalisierungsfehler, gemessen durch eine gemischte Trainings-Test-Aufteilung, ist zu optimistisch. Die Generalisierung durch eine zeitbasierte Aufteilung ist wahrscheinlich repräsentativer für die tatsächliche Leistung des Regressionsmodells. Lassen Sie uns diese Variabilität unserer Fehlerauswertung mit einer ordnungsgemäßen Kreuzvalidierung bewerten.
from sklearn.model_selection import cross_val_score
cv_mape_scores = -cross_val_score(
model, X, y, cv=ts_cv, scoring="neg_mean_absolute_percentage_error"
)
cv_mape_scores
array([0.44300752, 0.27772182, 0.3697178 ])
Die Variabilität zwischen den Aufteilungen ist ziemlich groß! In einer realen Situation wäre es ratsam, mehr Aufteilungen zu verwenden, um die Variabilität besser zu bewerten. Lassen Sie uns von nun an die mittleren CV-Scores und ihre Standardabweichung berichten.
print(f"CV MAPE: {cv_mape_scores.mean():.3f} ± {cv_mape_scores.std():.3f}")
CV MAPE: 0.363 ± 0.068
Wir können verschiedene Kombinationen von Bewertungsmetriken und Verlustfunktionen berechnen, die etwas weiter unten aufgeführt sind.
from collections import defaultdict
from sklearn.metrics import (
make_scorer,
mean_absolute_error,
mean_pinball_loss,
root_mean_squared_error,
)
from sklearn.model_selection import cross_validate
def consolidate_scores(cv_results, scores, metric):
if metric == "MAPE":
scores[metric].append(f"{value.mean():.2f} ± {value.std():.2f}")
else:
scores[metric].append(f"{value.mean():.1f} ± {value.std():.1f}")
return scores
scoring = {
"MAPE": make_scorer(mean_absolute_percentage_error),
"RMSE": make_scorer(root_mean_squared_error),
"MAE": make_scorer(mean_absolute_error),
"pinball_loss_05": make_scorer(mean_pinball_loss, alpha=0.05),
"pinball_loss_50": make_scorer(mean_pinball_loss, alpha=0.50),
"pinball_loss_95": make_scorer(mean_pinball_loss, alpha=0.95),
}
loss_functions = ["squared_error", "poisson", "absolute_error"]
scores = defaultdict(list)
for loss_func in loss_functions:
model = HistGradientBoostingRegressor(loss=loss_func)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["loss"].append(loss_func)
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
Modellierung der prädiktiven Unsicherheit durch Quantilregression#
Anstatt den Erwartungswert der Verteilung von \(Y|X\) zu modellieren, wie es die Methode der kleinsten Quadrate und Poisson-Verluste tun, könnte man versuchen, Quantile der bedingten Verteilung zu schätzen.
\(Y|X=x_i\) wird für einen gegebenen Datenpunkt \(x_i\) als Zufallsvariable erwartet, da wir davon ausgehen, dass die Anzahl der Ausleihen nicht zu 100 % genau aus den Merkmalen vorhergesagt werden kann. Sie kann durch andere Variablen beeinflusst werden, die von den vorhandenen verzögerten Merkmalen nicht richtig erfasst werden. Zum Beispiel kann nicht vollständig vorhergesagt werden, ob es in der nächsten Stunde regnen wird, anhand der Fahrradverleihdaten der vergangenen Stunden. Dies nennt man aleatorische Unsicherheit.
Quantilregression ermöglicht eine feinere Beschreibung dieser Verteilung, ohne starke Annahmen über ihre Form zu treffen.
quantile_list = [0.05, 0.5, 0.95]
for quantile in quantile_list:
model = HistGradientBoostingRegressor(loss="quantile", quantile=quantile)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
scores["loss"].append(f"quantile {int(quantile * 100)}")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
scores_df = pl.DataFrame(scores)
scores_df
Werfen wir einen Blick auf die Verluste, die jede Metrik minimieren.
def min_arg(col):
col_split = pl.col(col).str.split(" ")
return pl.arg_sort_by(
col_split.list.get(0).cast(pl.Float64),
col_split.list.get(2).cast(pl.Float64),
).first()
scores_df.select(
pl.col("loss").get(min_arg(col_name)).alias(col_name)
for col_name in scores_df.columns
if col_name != "loss"
)
Auch wenn sich die Score-Verteilungen aufgrund der Varianz im Datensatz überschneiden, ist es richtig, dass der durchschnittliche RMSE niedriger ist, wenn loss="squared_error", während der durchschnittliche MAPE niedriger ist, wenn loss="absolute_error", wie erwartet. Dies gilt auch für den Mean Pinball Loss mit den Quantilen 5 und 95. Der Score, der dem Quantilverlust 50 entspricht, überschneidet sich mit dem Score, der durch die Minimierung anderer Verlustfunktionen erzielt wird, was auch für die MAE gilt.
Qualitativer Blick auf die Vorhersagen#
Wir können nun die Leistung des Modells im Hinblick auf das 5. Perzentil, den Median und das 95. Perzentil visualisieren.
all_splits = list(ts_cv.split(X, y))
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
max_iter = 50
gbrt_mean_poisson = HistGradientBoostingRegressor(loss="poisson", max_iter=max_iter)
gbrt_mean_poisson.fit(X_train, y_train)
mean_predictions = gbrt_mean_poisson.predict(X_test)
gbrt_median = HistGradientBoostingRegressor(
loss="quantile", quantile=0.5, max_iter=max_iter
)
gbrt_median.fit(X_train, y_train)
median_predictions = gbrt_median.predict(X_test)
gbrt_percentile_5 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.05, max_iter=max_iter
)
gbrt_percentile_5.fit(X_train, y_train)
percentile_5_predictions = gbrt_percentile_5.predict(X_test)
gbrt_percentile_95 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.95, max_iter=max_iter
)
gbrt_percentile_95.fit(X_train, y_train)
percentile_95_predictions = gbrt_percentile_95.predict(X_test)
Wir können nun die von den Regressionsmodellen erstellten Vorhersagen betrachten.
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(15, 7))
plt.title("Predictions by regression models")
ax.plot(
y_test[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
median_predictions[last_hours],
"^-",
label="GBRT median",
)
ax.plot(
mean_predictions[last_hours],
"x-",
label="GBRT mean (Poisson)",
)
ax.fill_between(
np.arange(96),
percentile_5_predictions[last_hours],
percentile_95_predictions[last_hours],
alpha=0.3,
label="GBRT 90% interval",
)
_ = ax.legend()
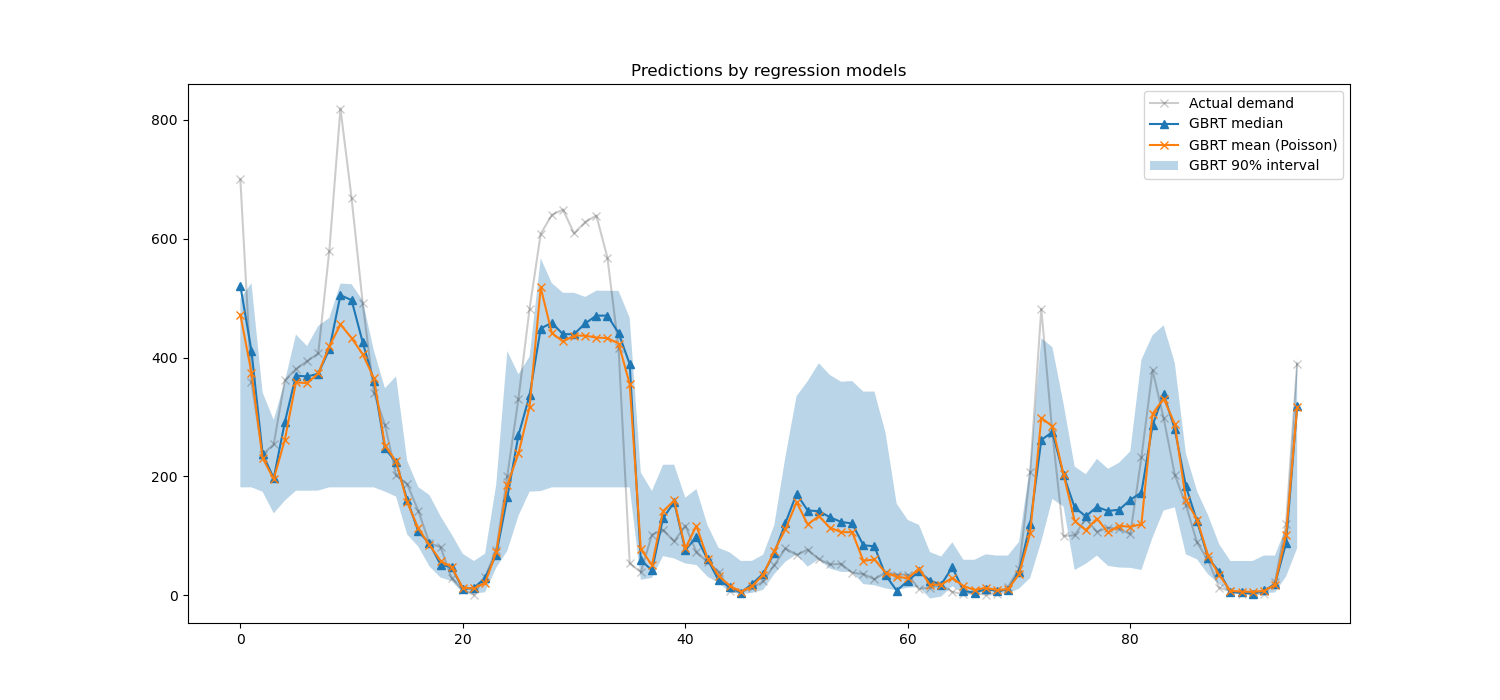
Hier ist es interessant zu bemerken, dass die blaue Fläche zwischen den Schätzern des 5 %- und 95 %-Perzentils eine Breite aufweist, die mit der Tageszeit variiert.
Nachts ist das blaue Band viel enger: Das Modellpaar ist sich ziemlich sicher, dass es eine geringe Anzahl von Fahrradverleihvorgängen geben wird. Und darüber hinaus scheinen diese korrekt zu sein, da die tatsächliche Nachfrage innerhalb dieses blauen Bandes bleibt.
Tagsüber ist das blaue Band viel breiter: Die Unsicherheit wächst, wahrscheinlich aufgrund der Wettervariabilität, die insbesondere an Wochenenden einen sehr großen Einfluss haben kann.
Wir können auch sehen, dass während der Wochentage das Pendelmuster noch im 5% und 95% Schätzer sichtbar ist.
Schließlich ist zu erwarten, dass 10 % der Zeit die tatsächliche Nachfrage nicht zwischen den Schätzungen des 5 %- und 95 %-Perzentils liegt. In dieser Testspanne scheint die tatsächliche Nachfrage höher zu sein, insbesondere während der Stoßzeiten. Dies könnte darauf hindeuten, dass unser 95%-Perzentilschätzer die Nachfragespitzen unterschätzt. Dies könnte quantitativ durch die Berechnung empirischer Abdeckungszahlen bestätigt werden, wie im Abschnitt Kalibrierung von Konfidenzintervallen durchgeführt.
Betrachtung der Leistung von nicht-linearen Regressionsmodellen im Vergleich zu den besten Modellen.
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(ncols=3, figsize=(15, 6), sharey=True)
fig.suptitle("Non-linear regression models")
predictions = [
median_predictions,
percentile_5_predictions,
percentile_95_predictions,
]
labels = [
"Median",
"5th percentile",
"95th percentile",
]
for ax, pred, label in zip(axes, predictions, labels):
PredictionErrorDisplay.from_predictions(
y_true=y_test,
y_pred=pred,
kind="residual_vs_predicted",
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set(xlabel="Predicted demand", ylabel="True demand")
ax.legend(["Best model", label])
plt.show()
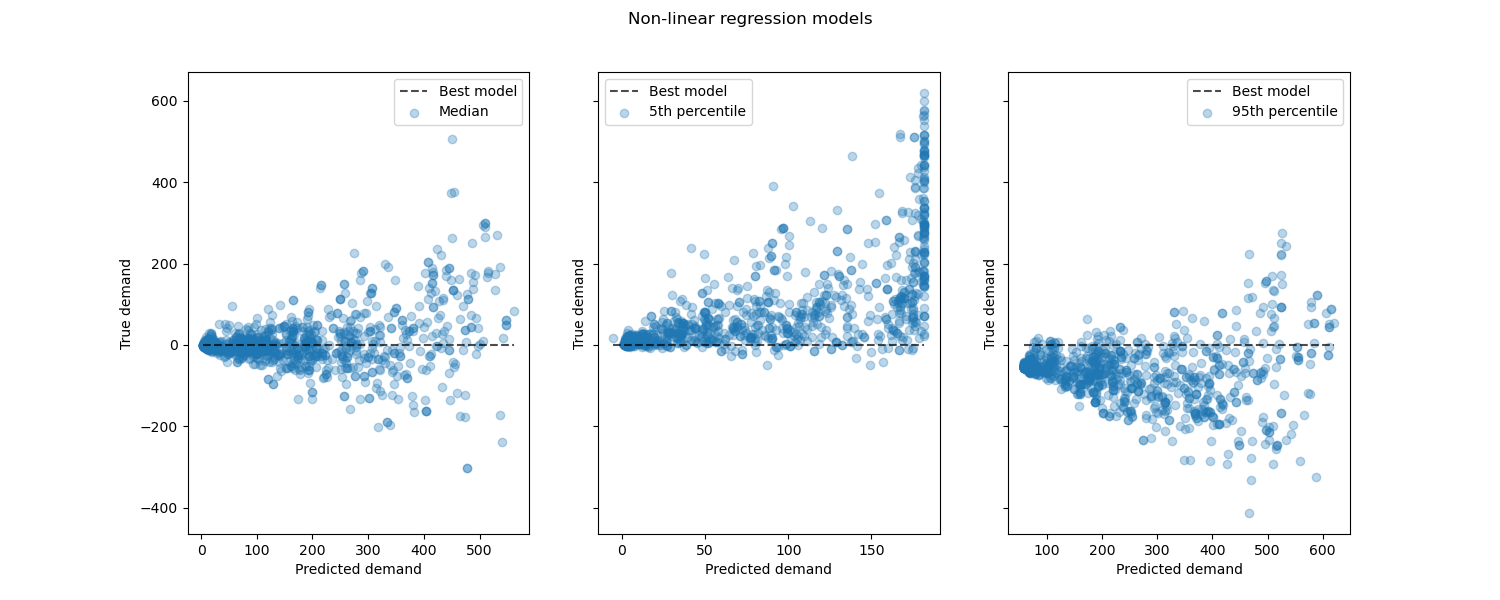
Schlussfolgerung#
In diesem Beispiel haben wir Zeitreihenprognosen mit verzögerten Merkmalen untersucht. Wir verglichen eine naive Regression (mit der standardisierten train_test_split) mit einer ordnungsgemäßen Zeitreihenbewertungsstrategie mit TimeSeriesSplit. Wir beobachteten, dass das mit train_test_split trainierte Modell mit einem Standardwert von shuffle auf True einen übermäßig optimistischen Mean Average Percentage Error (MAPE) ergab. Die Ergebnisse der zeitbasierten Aufteilung stellen die Leistung unseres Zeitreihen-Regressionsmodells besser dar. Wir analysierten auch die prädiktive Unsicherheit unseres Modells durch Quantilregression. Vorhersagen basierend auf dem 5. und 95. Perzentil mit loss="quantile" liefern uns eine quantitative Schätzung der Unsicherheit der Prognosen unseres Zeitreihen-Regressionsmodells. Unsicherheitsschätzungen können auch mit MAPIE durchgeführt werden, das eine Implementierung bietet, die auf neueren Arbeiten zu konformen Vorhersagemethoden basiert und sowohl aleatorische als auch epistemische Unsicherheit gleichzeitig schätzt. Darüber hinaus können Funktionalitäten von sktime verwendet werden, um scikit-learn-Schätzer zu erweitern, indem rekursive Zeitreihenprognosen genutzt werden, die dynamische Vorhersagen zukünftiger Werte ermöglichen.
Gesamtlaufzeit des Skripts: (0 Minuten 8,489 Sekunden)
Verwandte Beispiele
Modellkomplexität und kreuzvalidierter Score ausbalancieren
Vorhersageintervalle für Gradient Boosting Regression