Gewöhnliche kleinste Quadrate und Ridge-Regression

1. Gewöhnliche kleinste Quadrate (OLS): Wir veranschaulichen, wie das OLS-Modell LinearRegression auf einem einzelnen Merkmal des Diabetes-Datensatzes verwendet wird. Wir trainieren auf einem Teildatensatz, werten ihn auf einem Testdatensatz aus und visualisieren die Vorhersagen.

2. Gewöhnliche kleinste Quadrate und Ridge-Regression Varianz: Wir zeigen dann, wie OLS eine hohe Varianz aufweisen kann, wenn die Daten spärlich oder verrauscht sind, indem wir wiederholt auf einer sehr kleinen synthetischen Stichprobe trainieren. Die Ridge-Regression Ridge reduziert diese Varianz, indem sie die Koeffizienten bestraft (schrumpft), was zu stabileren Vorhersagen führt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Daten laden und vorbereiten

Laden Sie den Diabetes-Datensatz. Der Einfachheit halber behalten wir nur ein einzelnes Merkmal in den Daten bei. Dann teilen wir die Daten und das Ziel in Trainings- und Testdatensätze auf.

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split

X, y = load_diabetes(return_X_y=True)
X = X[:, [2]]  # Use only one feature
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, shuffle=False)

Lineares Regressionsmodell

Wir erstellen ein lineares Regressionsmodell und trainieren es auf den Trainingsdaten. Beachten Sie, dass standardmäßig ein Achsenabschnitt zum Modell hinzugefügt wird. Dieses Verhalten können wir durch Setzen des Parameters fit_intercept steuern.

from sklearn.linear_model import LinearRegression

regressor = LinearRegression().fit(X_train, y_train)

Modellevaluierung

Wir bewerten die Leistung des Modells auf dem Testdatensatz anhand des mittleren quadratischen Fehlers und des Bestimmtheitsmaßes.

from sklearn.metrics import mean_squared_error, r2_score

y_pred = regressor.predict(X_test)

print(f"Mean squared error: {mean_squared_error(y_test, y_pred):.2f}")
print(f"Coefficient of determination: {r2_score(y_test, y_pred):.2f}")

Mean squared error: 2548.07
Coefficient of determination: 0.47

Ergebnisse plotten

Schließlich visualisieren wir die Ergebnisse auf den Trainings- und Testdaten.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].scatter(X_train, y_train, label="Train data points")
ax[0].plot(
    X_train,
    regressor.predict(X_train),
    linewidth=3,
    color="tab:orange",
    label="Model predictions",
)
ax[0].set(xlabel="Feature", ylabel="Target", title="Train set")
ax[0].legend()

ax[1].scatter(X_test, y_test, label="Test data points")
ax[1].plot(X_test, y_pred, linewidth=3, color="tab:orange", label="Model predictions")
ax[1].set(xlabel="Feature", ylabel="Target", title="Test set")
ax[1].legend()

fig.suptitle("Linear Regression")

plt.show()

OLS auf dieser Ein-Merkmal-Untermenge lernt eine lineare Funktion, die den mittleren quadratischen Fehler auf den Trainingsdaten minimiert. Wir können sehen, wie gut (oder schlecht) sie generalisiert, indem wir uns den R^2-Score und den mittleren quadratischen Fehler auf dem Testdatensatz ansehen. In höheren Dimensionen neigt reines OLS oft zu Überanpassung, insbesondere wenn die Daten verrauscht sind. Regularisierungstechniken (wie Ridge oder Lasso) können dabei helfen.

Gewöhnliche kleinste Quadrate und Ridge-Regression Varianz

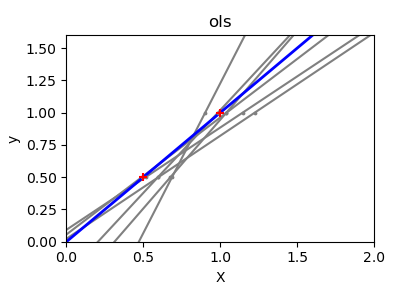
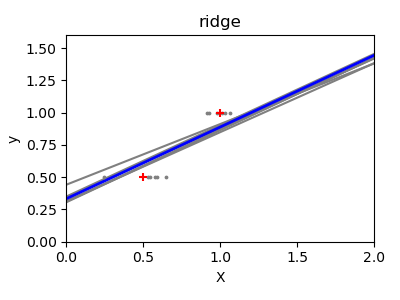
Als Nächstes veranschaulichen wir das Problem der hohen Varianz deutlicher anhand eines winzigen synthetischen Datensatzes. Wir ziehen nur zwei Datenpunkte und fügen ihnen wiederholt kleines Gaußsches Rauschen hinzu und trainieren sowohl OLS als auch Ridge neu. Wir plotten jede neue Linie, um zu sehen, wie stark OLS schwanken kann, während Ridge dank seines Strafterms stabiler bleibt.

import matplotlib.pyplot as plt
import numpy as np

from sklearn import linear_model

X_train = np.c_[0.5, 1].T
y_train = [0.5, 1]
X_test = np.c_[0, 2].T

np.random.seed(0)

classifiers = dict(
    ols=linear_model.LinearRegression(), ridge=linear_model.Ridge(alpha=0.1)
)

for name, clf in classifiers.items():
    fig, ax = plt.subplots(figsize=(4, 3))

    for _ in range(6):
        this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
        clf.fit(this_X, y_train)

        ax.plot(X_test, clf.predict(X_test), color="gray")
        ax.scatter(this_X, y_train, s=3, c="gray", marker="o", zorder=10)

    clf.fit(X_train, y_train)
    ax.plot(X_test, clf.predict(X_test), linewidth=2, color="blue")
    ax.scatter(X_train, y_train, s=30, c="red", marker="+", zorder=10)

    ax.set_title(name)
    ax.set_xlim(0, 2)
    ax.set_ylim((0, 1.6))
    ax.set_xlabel("X")
    ax.set_ylabel("y")

    fig.tight_layout()

plt.show()

• 
• 

Schlussfolgerung

• Im ersten Beispiel haben wir OLS auf einen realen Datensatz angewendet und gezeigt, wie ein einfaches lineares Modell die Daten durch Minimierung des quadrierten Fehlers auf dem Trainingsdatensatz anpassen kann.

• Im zweiten Beispiel schwankten die OLS-Linien jedes Mal drastisch, wenn Rauschen hinzugefügt wurde, was seine hohe Varianz bei spärlichen oder verrauschten Daten widerspiegelt. Im Gegensatz dazu führt die **Ridge**-Regression einen Regularisierungsterm ein, der die Koeffizienten schrumpfen lässt und die Vorhersagen stabilisiert.

Techniken wie Ridge oder Lasso (das eine L1-Strafe anwendet) sind beides gängige Methoden zur Verbesserung der Generalisierung und zur Reduzierung der Überanpassung. Ein gut abgestimmtes Ridge oder Lasso übertrifft reines OLS oft, wenn Merkmale korreliert sind, die Daten verrauscht sind oder die Stichprobengröße klein ist.

Verwandte Beispiele

Nicht-negative kleinste Quadrate

Nicht-negative kleinste Quadrate

Ridge-Koeffizienten als Funktion der Regularisierung plotten

Ridge-Koeffizienten als Funktion der Regularisierung plotten

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

Vergleich von Kernel Ridge und Gauß-Prozess-Regression

Vergleich von Kernel Ridge und Gauß-Prozess-Regression