Hinweis

Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

Ledoit-Wolf vs OAS-Schätzung#

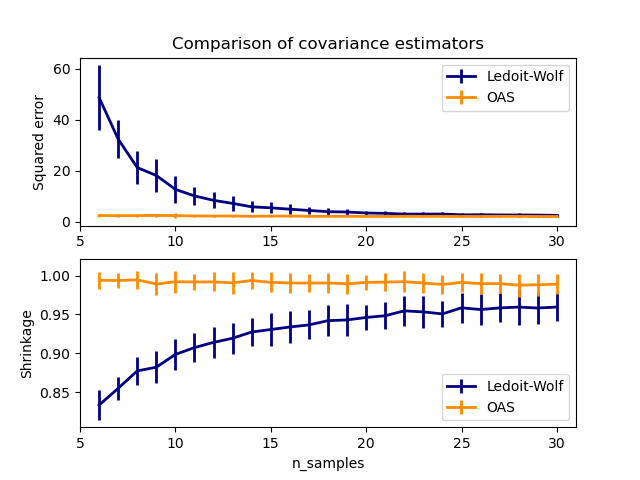
Die übliche Maximum-Likelihood-Schätzung der Kovarianz kann durch Schrumpfung regularisiert werden. Ledoit und Wolf schlugen eine geschlossene Formel vor, um den asymptotisch optimalen Schrumpfungsparameter zu berechnen (der ein MSE-Kriterium minimiert), was zu der Ledoit-Wolf-Kovarianzschätzung führt.

Chen et al. [1] schlugen eine Verbesserung des Ledoit-Wolf-Schrumpfungsparameters vor, den OAS-Koeffizienten, dessen Konvergenz unter der Annahme, dass die Daten Gaußsch verteilt sind, signifikant besser ist.

Dieses Beispiel, inspiriert von Chen's Veröffentlichung [1], zeigt einen Vergleich der geschätzten MSE der LW- und OAS-Methoden unter Verwendung von Gaußsch verteilten Daten.

Referenzen

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from scipy.linalg import cholesky, toeplitz

from sklearn.covariance import OAS, LedoitWolf

np.random.seed(0)

n_features = 100
# simulation covariance matrix (AR(1) process)
r = 0.1
real_cov = toeplitz(r ** np.arange(n_features))
coloring_matrix = cholesky(real_cov)

n_samples_range = np.arange(6, 31, 1)
repeat = 100
lw_mse = np.zeros((n_samples_range.size, repeat))
oa_mse = np.zeros((n_samples_range.size, repeat))
lw_shrinkage = np.zeros((n_samples_range.size, repeat))
oa_shrinkage = np.zeros((n_samples_range.size, repeat))
for i, n_samples in enumerate(n_samples_range):
    for j in range(repeat):
        X = np.dot(np.random.normal(size=(n_samples, n_features)), coloring_matrix.T)

        lw = LedoitWolf(store_precision=False, assume_centered=True)
        lw.fit(X)
        lw_mse[i, j] = lw.error_norm(real_cov, scaling=False)
        lw_shrinkage[i, j] = lw.shrinkage_

        oa = OAS(store_precision=False, assume_centered=True)
        oa.fit(X)
        oa_mse[i, j] = oa.error_norm(real_cov, scaling=False)
        oa_shrinkage[i, j] = oa.shrinkage_

# plot MSE
plt.subplot(2, 1, 1)
plt.errorbar(
    n_samples_range,
    lw_mse.mean(1),
    yerr=lw_mse.std(1),
    label="Ledoit-Wolf",
    color="navy",
    lw=2,
)
plt.errorbar(
    n_samples_range,
    oa_mse.mean(1),
    yerr=oa_mse.std(1),
    label="OAS",
    color="darkorange",
    lw=2,
)
plt.ylabel("Squared error")
plt.legend(loc="upper right")
plt.title("Comparison of covariance estimators")
plt.xlim(5, 31)

# plot shrinkage coefficient
plt.subplot(2, 1, 2)
plt.errorbar(
    n_samples_range,
    lw_shrinkage.mean(1),
    yerr=lw_shrinkage.std(1),
    label="Ledoit-Wolf",
    color="navy",
    lw=2,
)
plt.errorbar(
    n_samples_range,
    oa_shrinkage.mean(1),
    yerr=oa_shrinkage.std(1),
    label="OAS",
    color="darkorange",
    lw=2,
)
plt.xlabel("n_samples")
plt.ylabel("Shrinkage")
plt.legend(loc="lower right")
plt.ylim(plt.ylim()[0], 1.0 + (plt.ylim()[1] - plt.ylim()[0]) / 10.0)
plt.xlim(5, 31)

plt.show()

Gesamtlaufzeit des Skripts: (0 Minuten 2,252 Sekunden)

Verwandte Beispiele

Schrumpfkovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood

Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Robuste vs. Empirische Kovarianzschätzung

Schwachstellen-Inverse Kovarianzschätzung

Galerie generiert von Sphinx-Gallery

Ledoit-Wolf vs OAS-Schätzung#

Diese Seite