Übersicht über Meta-Estimators für Multiklassen-Training

In diesem Beispiel besprechen wir das Problem der Klassifizierung, wenn die Zielvariable aus mehr als zwei Klassen besteht. Dies wird als Multiklassen-Klassifizierung bezeichnet.

In scikit-learn unterstützen alle Estimators Multiklassen-Klassifizierung "out of the box": Die sinnvollste Strategie wurde für den Endbenutzer implementiert. Das Modul sklearn.multiclass implementiert verschiedene Strategien, die man zum Experimentieren oder zur Entwicklung von Drittanbieter-Estimators, die nur Binärklassifizierung unterstützen, verwenden kann.

sklearn.multiclass umfasst OvO/OvR-Strategien, die zum Trainieren eines Multiklassen-Klassifikators durch Anpassen einer Reihe von Binärklassifikatoren (die Meta-Estimators OneVsOneClassifier und OneVsRestClassifier) verwendet werden. Dieses Beispiel wird sie überprüfen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Der Yeast UCI Datensatz

In diesem Beispiel verwenden wir einen UCI-Datensatz [1], der allgemein als Yeast-Datensatz bezeichnet wird. Wir verwenden die Funktion sklearn.datasets.fetch_openml, um den Datensatz von OpenML zu laden.

from sklearn.datasets import fetch_openml

X, y = fetch_openml(data_id=181, as_frame=True, return_X_y=True)

Um die Art des datenwissenschaftlichen Problems zu kennen, mit dem wir es zu tun haben, können wir das Ziel überprüfen, für das wir ein Vorhersagemodell erstellen möchten.

y.value_counts().sort_index()

class_protein_localization
CYT    463
ERL      5
EXC     35
ME1     44
ME2     51
ME3    163
MIT    244
NUC    429
POX     20
VAC     30
Name: count, dtype: int64

Wir sehen, dass das Ziel diskret ist und aus 10 Klassen besteht. Wir haben es daher mit einem Multiklassen-Klassifizierungsproblem zu tun.

Vergleich von Strategien

Im folgenden Experiment verwenden wir einen DecisionTreeClassifier und eine RepeatedStratifiedKFold Kreuzvalidierung mit 3 Splits und 5 Wiederholungen.

Wir vergleichen die folgenden Strategien

• DecisionTreeClassifier kann Multiklassen-Klassifizierung ohne spezielle Anpassungen handhaben. Er funktioniert, indem er die Trainingsdaten in kleinere Teilmengen aufteilt und sich auf die häufigste Klasse in jeder Teilmenge konzentriert. Durch Wiederholung dieses Prozesses kann das Modell Eingabedaten genau in mehrere verschiedene Klassen klassifizieren.

• OneVsOneClassifier trainiert eine Reihe von Binärklassifikatoren, bei denen jeder Klassifikator trainiert wird, um zwischen zwei Klassen zu unterscheiden.

• OneVsRestClassifier: Trainiert eine Reihe von Binärklassifikatoren, bei denen jeder Klassifikator trainiert wird, um eine Klasse von den restlichen Klassen zu unterscheiden.

• OutputCodeClassifier: Trainiert eine Reihe von Binärklassifikatoren, bei denen jeder Klassifikator trainiert wird, um zwischen einer Menge von Klassen und den restlichen Klassen zu unterscheiden. Die Menge der Klassen wird durch ein Codebuch definiert, das in scikit-learn zufällig generiert wird. Diese Methode stellt den Parameter code_size zur Verfügung, um die Größe des Codebuchs zu steuern. Wir setzen ihn über eins, da wir nicht an der Komprimierung der Klassendarstellung interessiert sind.

import pandas as pd

from sklearn.model_selection import RepeatedStratifiedKFold, cross_validate
from sklearn.multiclass import (
    OneVsOneClassifier,
    OneVsRestClassifier,
    OutputCodeClassifier,
)
from sklearn.tree import DecisionTreeClassifier

cv = RepeatedStratifiedKFold(n_splits=3, n_repeats=5, random_state=0)

tree = DecisionTreeClassifier(random_state=0)
ovo_tree = OneVsOneClassifier(tree)
ovr_tree = OneVsRestClassifier(tree)
ecoc = OutputCodeClassifier(tree, code_size=2)

cv_results_tree = cross_validate(tree, X, y, cv=cv, n_jobs=2)
cv_results_ovo = cross_validate(ovo_tree, X, y, cv=cv, n_jobs=2)
cv_results_ovr = cross_validate(ovr_tree, X, y, cv=cv, n_jobs=2)
cv_results_ecoc = cross_validate(ecoc, X, y, cv=cv, n_jobs=2)

Wir können nun die statistische Leistung der verschiedenen Strategien vergleichen. Wir plotten die Ergebnisverteilung der verschiedenen Strategien.

from matplotlib import pyplot as plt

scores = pd.DataFrame(
    {
        "DecisionTreeClassifier": cv_results_tree["test_score"],
        "OneVsOneClassifier": cv_results_ovo["test_score"],
        "OneVsRestClassifier": cv_results_ovr["test_score"],
        "OutputCodeClassifier": cv_results_ecoc["test_score"],
    }
)
ax = scores.plot.kde(legend=True)
ax.set_xlabel("Accuracy score")
ax.set_xlim([0, 0.7])
_ = ax.set_title(
    "Density of the accuracy scores for the different multiclass strategies"
)

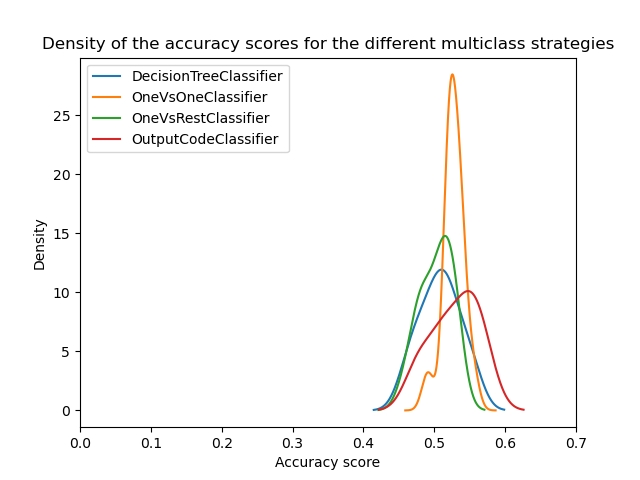
Auf den ersten Blick können wir sehen, dass die integrierte Strategie des Entscheidungsbaum-Klassifikators recht gut funktioniert. One-vs-one und die Fehlerkorrektur-Output-Code-Strategien funktionieren sogar noch besser. Die One-vs-rest-Strategie funktioniert jedoch nicht so gut wie die anderen Strategien.

Tatsächlich reproduzieren diese Ergebnisse etwas, das in der Literatur berichtet wird, wie in [2]. Die Geschichte ist jedoch nicht so einfach, wie sie scheint.

Die Bedeutung der Hyperparameter-Suche

Es wurde später in [3] gezeigt, dass die Multiklassen-Strategien ähnliche Ergebnisse zeigen würden, wenn die Hyperparameter der Basisklassifikatoren zuerst optimiert werden.

Hier versuchen wir, ein solches Ergebnis zu reproduzieren, indem wir zumindest die Tiefe des zugrundeliegenden Entscheidungsbaums optimieren.

from sklearn.model_selection import GridSearchCV

param_grid = {"max_depth": [3, 5, 8]}
tree_optimized = GridSearchCV(tree, param_grid=param_grid, cv=3)
ovo_tree = OneVsOneClassifier(tree_optimized)
ovr_tree = OneVsRestClassifier(tree_optimized)
ecoc = OutputCodeClassifier(tree_optimized, code_size=2)

cv_results_tree = cross_validate(tree_optimized, X, y, cv=cv, n_jobs=2)
cv_results_ovo = cross_validate(ovo_tree, X, y, cv=cv, n_jobs=2)
cv_results_ovr = cross_validate(ovr_tree, X, y, cv=cv, n_jobs=2)
cv_results_ecoc = cross_validate(ecoc, X, y, cv=cv, n_jobs=2)

scores = pd.DataFrame(
    {
        "DecisionTreeClassifier": cv_results_tree["test_score"],
        "OneVsOneClassifier": cv_results_ovo["test_score"],
        "OneVsRestClassifier": cv_results_ovr["test_score"],
        "OutputCodeClassifier": cv_results_ecoc["test_score"],
    }
)
ax = scores.plot.kde(legend=True)
ax.set_xlabel("Accuracy score")
ax.set_xlim([0, 0.7])
_ = ax.set_title(
    "Density of the accuracy scores for the different multiclass strategies"
)

plt.show()

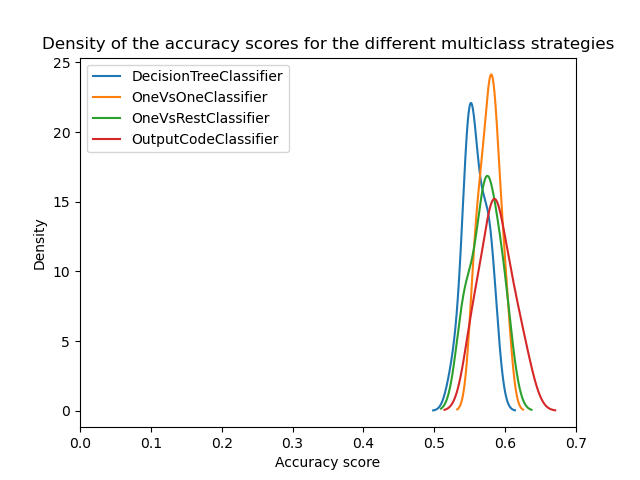
Wir können sehen, dass nach der Optimierung der Hyperparameter alle Multiklassen-Strategien ähnliche Leistungen erbringen, wie in [3] diskutiert.

Schlussfolgerung

Wir können einige Einblicke in diese Ergebnisse gewinnen.

Erstens liegt der Grund dafür, dass One-vs-one und Error-Correcting Output Code den Baum bei nicht optimierten Hyperparametern übertreffen, darin, dass sie eine größere Anzahl von Klassifikatoren aggregieren. Die Aggregation verbessert die Generalisierungsleistung. Dies ähnelt ein wenig dem Grund, warum ein Bagging-Klassifikator im Allgemeinen besser abschneidet als ein einzelner Entscheidungsbaum, wenn nicht auf die Optimierung der Hyperparameter geachtet wird.

Dann sehen wir die Bedeutung der Optimierung der Hyperparameter. Tatsächlich sollte dies regelmäßig bei der Entwicklung von Vorhersagemodellen untersucht werden, auch wenn Techniken wie Aggregation dazu beitragen, diese Auswirkungen zu reduzieren.

Schließlich ist es wichtig zu bedenken, dass die Estimators in scikit-learn mit einer spezifischen Strategie entwickelt werden, um Multiklassen-Klassifizierung "out of the box" zu handhaben. Für diese Estimators bedeutet dies, dass keine Notwendigkeit besteht, unterschiedliche Strategien zu verwenden. Diese Strategien sind hauptsächlich für Drittanbieter-Estimators nützlich, die nur Binärklassifizierung unterstützen. In allen Fällen zeigen wir auch, dass die Hyperparameter optimiert werden sollten.

Referenzen

[1]

https://archive.ics.uci.edu/ml/datasets/Yeast

[2]

„Reducing multiclass to binary: A unifying approach for margin classifiers.“ Allwein, Erin L., Robert E. Schapire, und Yoram Singer. Journal of machine learning research. 1. Dez. (2000): 113-141.

[3] (1,2)

„In defense of one-vs-all classification.“ Journal of Machine Learning Research. 5. Jan. (2004): 101-141.

Verwandte Beispiele

Verschachtelte vs. nicht verschachtelte Kreuzvalidierung

Verschachtelte vs. nicht verschachtelte Kreuzvalidierung

Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion

Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion

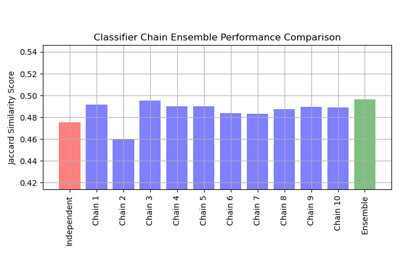
Multilabel-Klassifikation mit einem Klassifikator-Ketten

Multilabel-Klassifikation mit einem Klassifikator-Ketten

Entscheidungsgrenzen von multinomialer und One-vs-Rest Logistischer Regression

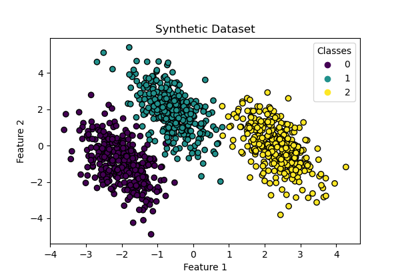
Entscheidungsgrenzen von multinomialer und One-vs-Rest Logistischer Regression