Hinweis
Gehen Sie zum Ende, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Vorhersage des CO2-Gehalts auf dem Mona Loa-Datensatz mit Gaußschem Prozess-Regression (GPR)#
Dieses Beispiel basiert auf Abschnitt 5.4.3 von „Gaussian Processes for Machine Learning“ [1]. Es illustriert ein Beispiel für komplexes Kernel-Engineering und Hyperparameter-Optimierung mittels Gradientenaufstieg auf der Log-Marginal-Likelihood. Die Daten bestehen aus den monatlichen Durchschnittskonzentrationen von atmosphärischem CO2 (in ppm – parts per million by volume), die zwischen 1958 und 2001 im Mauna Loa Observatory auf Hawaii gesammelt wurden. Ziel ist es, die CO2-Konzentration als Funktion der Zeit \(t\) zu modellieren und für die Jahre nach 2001 zu extrapolieren.
Referenzen
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Erstellung des Datensatzes#
Wir leiten einen Datensatz vom Mauna Loa Observatory ab, das Luftproben gesammelt hat. Wir sind daran interessiert, die CO2-Konzentration abzuschätzen und sie für weitere Jahre zu extrapolieren. Zuerst laden wir den ursprünglichen Datensatz, der auf OpenML verfügbar ist, als Pandas-DataFrame. Dieser wird durch Polars ersetzt, sobald fetch_openml native Unterstützung dafür hinzufügt.
from sklearn.datasets import fetch_openml
co2 = fetch_openml(data_id=41187, as_frame=True)
co2.frame.head()
Zuerst verarbeiten wir den ursprünglichen DataFrame, um eine Datumsspalte zu erstellen und diese zusammen mit der CO2-Spalte auszuwählen.
import polars as pl
co2_data = pl.DataFrame(co2.frame[["year", "month", "day", "co2"]]).select(
pl.date("year", "month", "day"), "co2"
)
co2_data.head()
co2_data["date"].min(), co2_data["date"].max()
(datetime.date(1958, 3, 29), datetime.date(2001, 12, 29))
Wir sehen, dass wir für einige Tage von März 1958 bis Dezember 2001 CO2-Konzentrationen erhalten. Wir können die Rohinformationen plotten, um ein besseres Verständnis zu bekommen.
import matplotlib.pyplot as plt
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("date")
plt.ylabel("CO$_2$ concentration (ppm)")
_ = plt.title("Raw air samples measurements from the Mauna Loa Observatory")
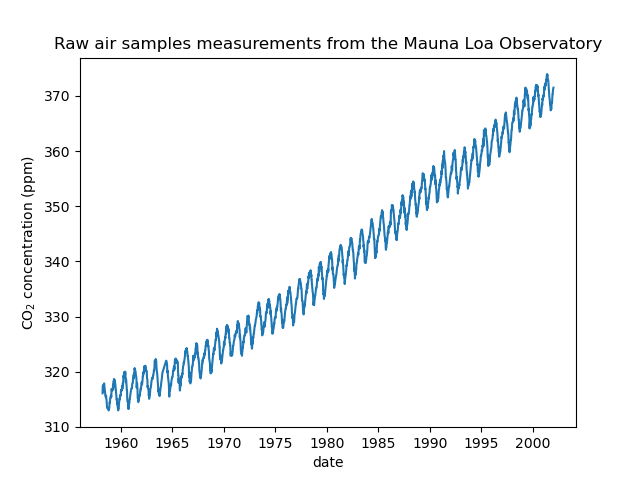
Wir werden den Datensatz vorverarbeiten, indem wir einen Monatsdurchschnitt bilden und Monate löschen, für die keine Messungen gesammelt wurden. Eine solche Verarbeitung hat einen Glättungseffekt auf die Daten.
co2_data = (
co2_data.sort(by="date")
.group_by_dynamic("date", every="1mo")
.agg(pl.col("co2").mean())
.drop_nulls()
)
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("date")
plt.ylabel("Monthly average of CO$_2$ concentration (ppm)")
_ = plt.title(
"Monthly average of air samples measurements\nfrom the Mauna Loa Observatory"
)
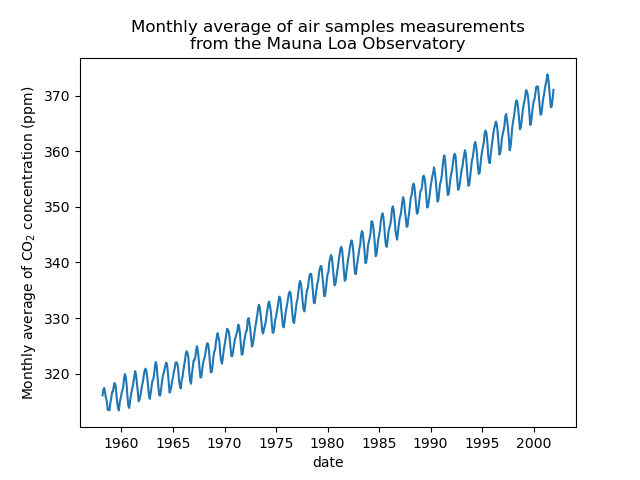
Die Idee in diesem Beispiel wird sein, die CO2-Konzentration in Abhängigkeit vom Datum vorherzusagen. Wir sind außerdem daran interessiert, für kommende Jahre nach 2001 zu extrapolieren.
Als ersten Schritt werden wir die Daten und das zu schätzende Ziel aufteilen. Da die Daten ein Datum sind, werden wir es in ein numerisches Format umwandeln.
X = co2_data.select(
pl.col("date").dt.year() + pl.col("date").dt.month() / 12
).to_numpy()
y = co2_data["co2"].to_numpy()
Gestaltung des passenden Kernels#
Um den Kernel für unseren Gaußschen Prozess zu gestalten, können wir einige Annahmen über die vorliegenden Daten treffen. Wir beobachten, dass sie mehrere Eigenschaften aufweisen: einen langfristigen aufsteigenden Trend, eine ausgeprägte saisonale Schwankung und einige kleinere Unregelmäßigkeiten. Wir können verschiedene geeignete Kernel verwenden, die diese Merkmale erfassen.
Erstens könnte der langfristige aufsteigende Trend mit einem Radial Basis Function (RBF)-Kernel mit einem großen Längenmaßparameter angepasst werden. Der RBF-Kernel mit einem großen Längenmaß erzwingt, dass diese Komponente glatt ist. Ein Trendanstieg wird nicht erzwungen, um unserem Modell einen Freiheitsgrad zu geben. Das spezifische Längenmaß und die Amplitude sind freie Hyperparameter.
Die saisonale Schwankung wird durch den periodischen Exponential Sine Squared-Kernel mit einer festen Periodizität von 1 Jahr erklärt. Das Längenmaß dieser periodischen Komponente, das ihre Glattheit steuert, ist ein freier Parameter. Um ein Abklingen von exakter Periodizität zu ermöglichen, wird das Produkt mit einem RBF-Kernel gebildet. Das Längenmaß dieser RBF-Komponente steuert die Abklingzeit und ist ein weiterer freier Parameter. Diese Art von Kernel wird auch als lokal periodischer Kernel bezeichnet.
from sklearn.gaussian_process.kernels import ExpSineSquared
seasonal_kernel = (
2.0**2
* RBF(length_scale=100.0)
* ExpSineSquared(length_scale=1.0, periodicity=1.0, periodicity_bounds="fixed")
)
Die kleinen Unregelmäßigkeiten sollen durch eine Rational Quadratic-Kernel-Komponente erklärt werden, deren Längenmaß und Alpha-Parameter, die die Streuung der Längenmaße quantifizieren, bestimmt werden müssen. Ein Rational Quadratic-Kernel ist äquivalent zu einem RBF-Kernel mit mehreren Längenmaßen und wird die verschiedenen Unregelmäßigkeiten besser berücksichtigen.
from sklearn.gaussian_process.kernels import RationalQuadratic
irregularities_kernel = 0.5**2 * RationalQuadratic(length_scale=1.0, alpha=1.0)
Schließlich kann das Rauschen im Datensatz mit einem Kernel berücksichtigt werden, der einen RBF-Kernel-Beitrag, der korrelierte Rauschkomponenten wie lokale Wetterphänomene erklären soll, und einen White-Kernel-Beitrag für das weiße Rauschen umfasst. Die relativen Amplituden und das Längenmaß des RBF sind weitere freie Parameter.
from sklearn.gaussian_process.kernels import WhiteKernel
noise_kernel = 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(
noise_level=0.1**2, noise_level_bounds=(1e-5, 1e5)
)
Somit ist unser endgültiger Kernel die Addition aller vorherigen Kernel.
co2_kernel = (
long_term_trend_kernel + seasonal_kernel + irregularities_kernel + noise_kernel
)
co2_kernel
50**2 * RBF(length_scale=50) + 2**2 * RBF(length_scale=100) * ExpSineSquared(length_scale=1, periodicity=1) + 0.5**2 * RationalQuadratic(alpha=1, length_scale=1) + 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(noise_level=0.01)
Modellanpassung und Extrapolation#
Nun sind wir bereit, einen Gaußschen Prozess-Regressor zu verwenden und die verfügbaren Daten anzupassen. Um dem Beispiel aus der Literatur zu folgen, werden wir den Mittelwert vom Ziel subtrahieren. Wir hätten normalize_y=True verwenden können. Dies hätte jedoch auch die Zielwerte skaliert (y durch seine Standardabweichung geteilt). Somit hätten die Hyperparameter der verschiedenen Kernel eine andere Bedeutung, da sie nicht in ppm ausgedrückt worden wären.
from sklearn.gaussian_process import GaussianProcessRegressor
y_mean = y.mean()
gaussian_process = GaussianProcessRegressor(kernel=co2_kernel, normalize_y=False)
gaussian_process.fit(X, y - y_mean)
Nun werden wir den Gaußschen Prozess verwenden, um auf
Trainingsdaten für die Überprüfung der Anpassungsgüte vorauszusagen;
zukünftige Daten, um die vom Modell durchgeführte Extrapolation zu sehen.
Daher erstellen wir synthetische Daten von 1958 bis zum aktuellen Monat. Zusätzlich müssen wir den während des Trainings subtrahierten Mittelwert hinzufügen.
import datetime
import numpy as np
today = datetime.datetime.now()
current_month = today.year + today.month / 12
X_test = np.linspace(start=1958, stop=current_month, num=1_000).reshape(-1, 1)
mean_y_pred, std_y_pred = gaussian_process.predict(X_test, return_std=True)
mean_y_pred += y_mean
plt.plot(X, y, color="black", linestyle="dashed", label="Measurements")
plt.plot(X_test, mean_y_pred, color="tab:blue", alpha=0.4, label="Gaussian process")
plt.fill_between(
X_test.ravel(),
mean_y_pred - std_y_pred,
mean_y_pred + std_y_pred,
color="tab:blue",
alpha=0.2,
)
plt.legend()
plt.xlabel("Year")
plt.ylabel("Monthly average of CO$_2$ concentration (ppm)")
_ = plt.title(
"Monthly average of air samples measurements\nfrom the Mauna Loa Observatory"
)
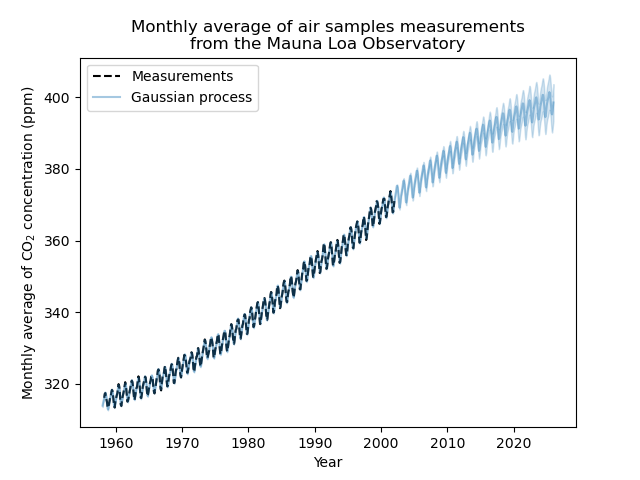
Unser angepasstes Modell ist in der Lage, frühere Daten korrekt anzupassen und mit Zuversicht in zukünftige Jahre zu extrapolieren.
Interpretation der Kernel-Hyperparameter#
Nun können wir uns die Hyperparameter des Kernels ansehen.
gaussian_process.kernel_
44.8**2 * RBF(length_scale=51.6) + 2.64**2 * RBF(length_scale=91.5) * ExpSineSquared(length_scale=1.48, periodicity=1) + 0.536**2 * RationalQuadratic(alpha=2.89, length_scale=0.968) + 0.188**2 * RBF(length_scale=0.122) + WhiteKernel(noise_level=0.0367)
Somit wird der größte Teil des Signals, nach Abzug des Mittelwerts, durch einen langfristigen aufsteigenden Trend für ca. 45 ppm und ein Längenmaß von ca. 52 Jahren erklärt. Die periodische Komponente hat eine Amplitude von ca. 2,6 ppm, eine Abklingzeit von ca. 90 Jahren und ein Längenmaß von ca. 1,5. Die lange Abklingzeit deutet darauf hin, dass wir eine Komponente haben, die sehr nah an einer saisonalen Periodizität liegt. Das korrelierte Rauschen hat eine Amplitude von ca. 0,2 ppm mit einem Längenmaß von ca. 0,12 Jahren und einen White-Noise-Beitrag von ca. 0,04 ppm. Somit ist das gesamte Rauschlevel sehr gering, was darauf hindeutet, dass die Daten durch das Modell sehr gut erklärt werden können.
Gesamtlaufzeit des Skripts: (0 Minuten 3,994 Sekunden)
Verwandte Beispiele
Gauß-Prozesse Regression: grundlegendes Einführungsexempel
Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels
Vergleich von Kernel Ridge und Gauß-Prozess-Regression
Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz