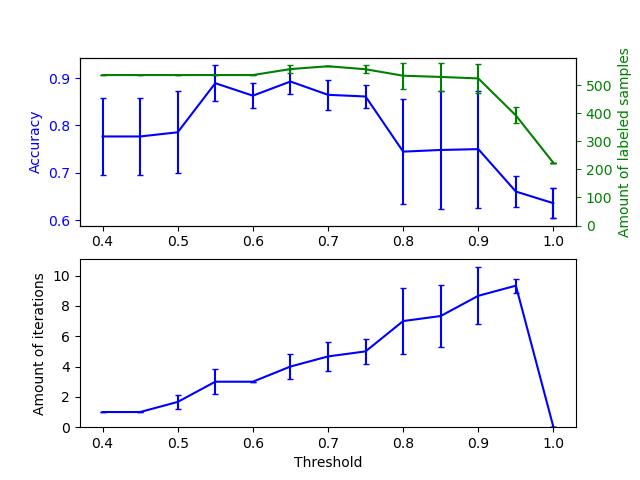
Auswirkung der Variierung des Schwellenwerts für das Selbsttraining

Dieses Beispiel veranschaulicht die Auswirkung eines variierenden Schwellenwerts auf das Selbsttraining. Der Datensatz breast_cancer wird geladen, und die Labels werden gelöscht, sodass nur 50 von 569 Stichproben Labels haben. Ein SelfTrainingClassifier wird auf diesem Datensatz mit variierenden Schwellenwerten angepasst.

Der obere Graph zeigt die Menge der gelabelten Stichproben, die dem Klassifikator am Ende des Fits zur Verfügung stehen, sowie die Genauigkeit des Klassifikators. Der untere Graph zeigt die letzte Iteration, in der eine Stichprobe gelabelt wurde. Alle Werte werden mit 3 Folds kreuzvalidiert.

Bei niedrigen Schwellenwerten (in [0.4, 0.5]) lernt der Klassifikator von Stichproben, die mit geringer Konfidenz gelabelt wurden. Diese Stichproben mit geringer Konfidenz haben wahrscheinlich falsche vorhergesagte Labels, und infolgedessen führt die Anpassung an diesen falschen Labels zu einer schlechten Genauigkeit. Beachten Sie, dass der Klassifikator fast alle Stichproben labelt und nur eine Iteration benötigt.

Bei sehr hohen Schwellenwerten (in [0.9, 1)) stellen wir fest, dass der Klassifikator seinen Datensatz nicht erweitert (die Menge der selbst gelabelten Stichproben beträgt 0). Infolgedessen ist die Genauigkeit, die mit einem Schwellenwert von 0,9999 erzielt wird, dieselbe wie die, die ein normaler überwachter Klassifikator erzielen würde.

Die optimale Genauigkeit liegt zwischen diesen beiden Extremen bei einem Schwellenwert von etwa 0,7.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.model_selection import StratifiedKFold
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC
from sklearn.utils import shuffle

n_splits = 3

X, y = datasets.load_breast_cancer(return_X_y=True)
X, y = shuffle(X, y, random_state=42)
y_true = y.copy()
y[50:] = -1
total_samples = y.shape[0]

base_classifier = SVC(probability=True, gamma=0.001, random_state=42)

x_values = np.arange(0.4, 1.05, 0.05)
x_values = np.append(x_values, 0.99999)
scores = np.empty((x_values.shape[0], n_splits))
amount_labeled = np.empty((x_values.shape[0], n_splits))
amount_iterations = np.empty((x_values.shape[0], n_splits))

for i, threshold in enumerate(x_values):
    self_training_clf = SelfTrainingClassifier(base_classifier, threshold=threshold)

    # We need manual cross validation so that we don't treat -1 as a separate
    # class when computing accuracy
    skfolds = StratifiedKFold(n_splits=n_splits)
    for fold, (train_index, test_index) in enumerate(skfolds.split(X, y)):
        X_train = X[train_index]
        y_train = y[train_index]
        X_test = X[test_index]
        y_test = y[test_index]
        y_test_true = y_true[test_index]

        self_training_clf.fit(X_train, y_train)

        # The amount of labeled samples that at the end of fitting
        amount_labeled[i, fold] = (
            total_samples
            - np.unique(self_training_clf.labeled_iter_, return_counts=True)[1][0]
        )
        # The last iteration the classifier labeled a sample in
        amount_iterations[i, fold] = np.max(self_training_clf.labeled_iter_)

        y_pred = self_training_clf.predict(X_test)
        scores[i, fold] = accuracy_score(y_test_true, y_pred)


ax1 = plt.subplot(211)
ax1.errorbar(
    x_values, scores.mean(axis=1), yerr=scores.std(axis=1), capsize=2, color="b"
)
ax1.set_ylabel("Accuracy", color="b")
ax1.tick_params("y", colors="b")

ax2 = ax1.twinx()
ax2.errorbar(
    x_values,
    amount_labeled.mean(axis=1),
    yerr=amount_labeled.std(axis=1),
    capsize=2,
    color="g",
)
ax2.set_ylim(bottom=0)
ax2.set_ylabel("Amount of labeled samples", color="g")
ax2.tick_params("y", colors="g")

ax3 = plt.subplot(212, sharex=ax1)
ax3.errorbar(
    x_values,
    amount_iterations.mean(axis=1),
    yerr=amount_iterations.std(axis=1),
    capsize=2,
    color="b",
)
ax3.set_ylim(bottom=0)
ax3.set_ylabel("Amount of iterations")
ax3.set_xlabel("Threshold")

plt.show()

Verwandte Beispiele

Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion

Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion

Entscheidungsgrenze semi-überwachter Klassifikatoren vs. SVM auf dem Iris-Datensatz

Entscheidungsgrenze semi-überwachter Klassifikatoren vs. SVM auf dem Iris-Datensatz

Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen

Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen

Semi-überwachte Klassifikation auf einem Textdatensatz

Semi-überwachte Klassifikation auf einem Textdatensatz