Swiss Roll und Swiss-Hole-Reduktion

Dieses Notebook vergleicht zwei beliebte nichtlineare Dimensionalitätstechniken, T-distributed Stochastic Neighbor Embedding (t-SNE) und Locally Linear Embedding (LLE), auf dem klassischen Swiss-Roll-Datensatz. Anschließend untersuchen wir, wie beide mit der Hinzufügung eines Lochs in den Daten umgehen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Swiss Roll

Wir beginnen mit der Generierung des Swiss-Roll-Datensatzes.

import matplotlib.pyplot as plt

from sklearn import datasets, manifold

sr_points, sr_color = datasets.make_swiss_roll(n_samples=1500, random_state=0)

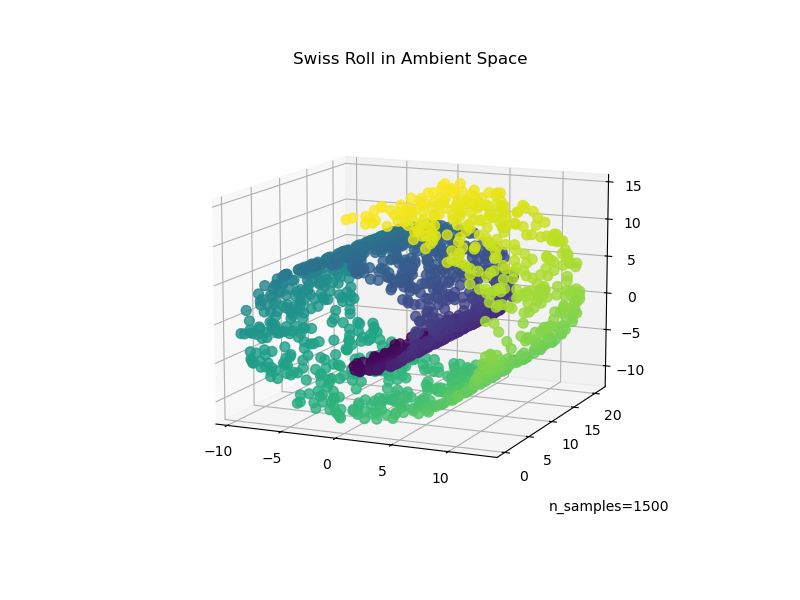
Nun werfen wir einen Blick auf unsere Daten

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sr_points[:, 0], sr_points[:, 1], sr_points[:, 2], c=sr_color, s=50, alpha=0.8
)
ax.set_title("Swiss Roll in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

Nachdem wir die LLE- und t-SNE-Einbettungen berechnet haben, stellen wir fest, dass LLE den Swiss Roll ziemlich effektiv entrollt. t-SNE hingegen ist in der Lage, die allgemeine Struktur der Daten zu erhalten, stellt jedoch die kontinuierliche Natur unserer ursprünglichen Daten schlecht dar. Stattdessen scheint es unnötigerweise Punkte zu gruppieren.

sr_lle, sr_err = manifold.locally_linear_embedding(
    sr_points, n_neighbors=12, n_components=2
)

sr_tsne = manifold.TSNE(n_components=2, perplexity=40, random_state=0).fit_transform(
    sr_points
)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sr_lle[:, 0], sr_lle[:, 1], c=sr_color)
axs[0].set_title("LLE Embedding of Swiss Roll")
axs[1].scatter(sr_tsne[:, 0], sr_tsne[:, 1], c=sr_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss Roll")

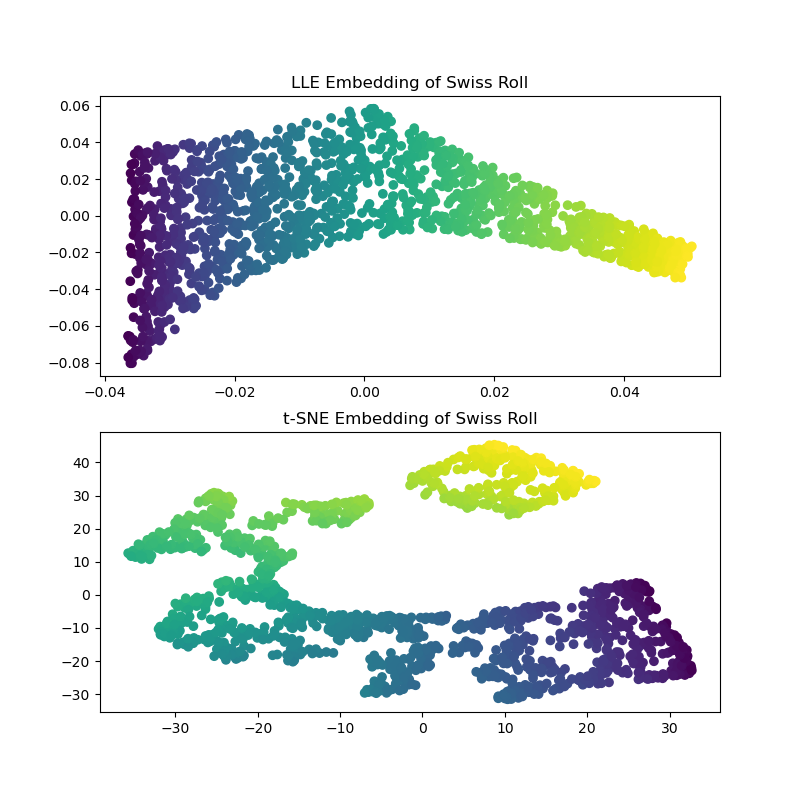
Hinweis

LLE scheint die Punkte vom Zentrum (lila) des Swiss Rolls zu strecken. Wir stellen jedoch fest, dass dies lediglich ein Nebenprodukt der Datengenerierung ist. In der Nähe des Zentrums des Rolls gibt es eine höhere Punktedichte, die letztendlich beeinflusst, wie LLE die Daten in einer niedrigeren Dimension rekonstruiert.

Swiss-Hole

Betrachten wir nun, wie beide Algorithmen damit umgehen, dass wir den Daten ein Loch hinzufügen. Zuerst generieren wir den Swiss-Hole-Datensatz und plotten ihn

sh_points, sh_color = datasets.make_swiss_roll(
    n_samples=1500, hole=True, random_state=0
)

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sh_points[:, 0], sh_points[:, 1], sh_points[:, 2], c=sh_color, s=50, alpha=0.8
)
ax.set_title("Swiss-Hole in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

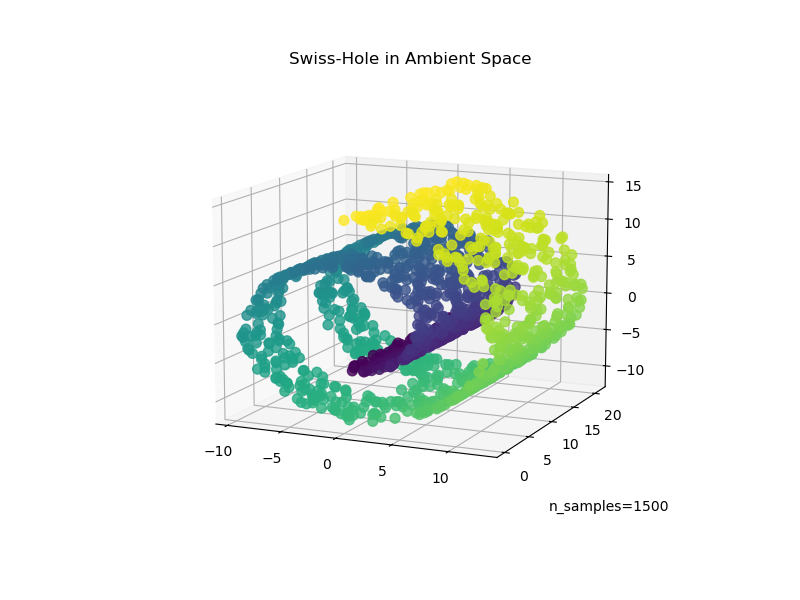
Bei der Berechnung der LLE- und t-SNE-Einbettungen erhalten wir ähnliche Ergebnisse wie beim Swiss Roll. LLE entrollt die Daten sehr fähig und erhält sogar das Loch. t-SNE gruppiert wieder Punkte, aber wir stellen fest, dass es die allgemeine Topologie der ursprünglichen Daten beibehält.

sh_lle, sh_err = manifold.locally_linear_embedding(
    sh_points, n_neighbors=12, n_components=2
)

sh_tsne = manifold.TSNE(
    n_components=2, perplexity=40, init="random", random_state=0
).fit_transform(sh_points)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sh_lle[:, 0], sh_lle[:, 1], c=sh_color)
axs[0].set_title("LLE Embedding of Swiss-Hole")
axs[1].scatter(sh_tsne[:, 0], sh_tsne[:, 1], c=sh_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss-Hole")

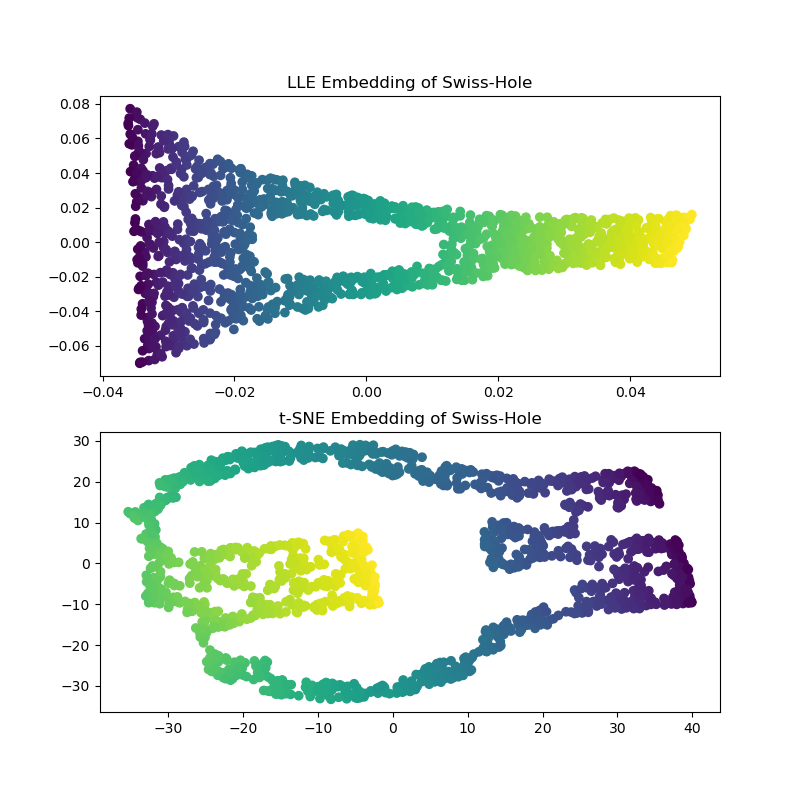
Schlussbemerkungen

Wir stellen fest, dass t-SNE von der Prüfung weiterer Parameterkombinationen profitiert. Durch eine bessere Abstimmung dieser Parameter könnten wahrscheinlich bessere Ergebnisse erzielt werden.

Wir stellen fest, dass t-SNE, wie im Beispiel "Manifold Learning auf handschriftlichen Ziffern" gezeigt, im Allgemeinen besser als LLE auf realen Daten funktioniert.

Verwandte Beispiele

Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

Mannigfaltigkeitslernen auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap...

Vergleich von Manifold Learning Methoden

Vergleich von Manifold Learning Methoden

Visualisierung der Aktienmarktstruktur

Visualisierung der Aktienmarktstruktur

Hierarchisches Clustering mit und ohne Struktur

Hierarchisches Clustering mit und ohne Struktur