Erkennung handgeschriebener Ziffern

Dieses Beispiel zeigt, wie scikit-learn zur Erkennung von Bildern handgeschriebener Ziffern von 0-9 verwendet werden kann.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

# Standard scientific Python imports
import matplotlib.pyplot as plt

# Import datasets, classifiers and performance metrics
from sklearn import datasets, metrics, svm
from sklearn.model_selection import train_test_split

Datensatz der Ziffern

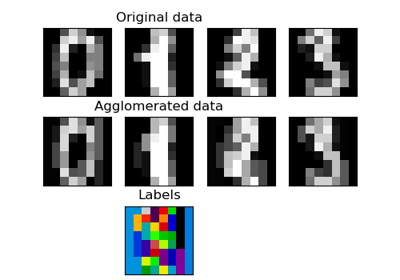
Der Datensatz der Ziffern besteht aus 8x8 Pixelbildern von Ziffern. Das images-Attribut des Datensatzes speichert 8x8-Arrays von Graustufenwerten für jedes Bild. Wir werden diese Arrays verwenden, um die ersten 4 Bilder zu visualisieren. Das target-Attribut des Datensatzes speichert die Ziffer, die jedes Bild darstellt, und dies ist in den Titeln der 4 unten stehenden Diagramme enthalten.

Hinweis: Wenn wir mit Bilddateien arbeiten würden (z. B. 'png'-Dateien), würden wir sie mit matplotlib.pyplot.imread laden.

digits = datasets.load_digits()

_, axes = plt.subplots(nrows=1, ncols=4, figsize=(10, 3))
for ax, image, label in zip(axes, digits.images, digits.target):
    ax.set_axis_off()
    ax.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
    ax.set_title("Training: %i" % label)

Klassifizierung

Um einen Klassifikator auf diese Daten anzuwenden, müssen wir die Bilder abflachen und jedes 2D-Array von Graustufenwerten von der Form (8, 8) in die Form (64,) umwandeln. Anschließend wird der gesamte Datensatz die Form (n_samples, n_features) haben, wobei n_samples die Anzahl der Bilder und n_features die Gesamtzahl der Pixel in jedem Bild ist.

Anschließend können wir die Daten in Trainings- und Testuntergruppen aufteilen und einen Support-Vektor-Klassifikator auf die Trainingsstichproben anwenden. Der angepasste Klassifikator kann anschließend verwendet werden, um den Wert der Ziffer für die Stichproben im Testunterdatensatz vorherzusagen.

# flatten the images
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))

# Create a classifier: a support vector classifier
clf = svm.SVC(gamma=0.001)

# Split data into 50% train and 50% test subsets
X_train, X_test, y_train, y_test = train_test_split(
    data, digits.target, test_size=0.5, shuffle=False
)

# Learn the digits on the train subset
clf.fit(X_train, y_train)

# Predict the value of the digit on the test subset
predicted = clf.predict(X_test)

Unten visualisieren wir die ersten 4 Teststichproben und zeigen ihren vorhergesagten Ziffernwert im Titel an.

_, axes = plt.subplots(nrows=1, ncols=4, figsize=(10, 3))
for ax, image, prediction in zip(axes, X_test, predicted):
    ax.set_axis_off()
    image = image.reshape(8, 8)
    ax.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
    ax.set_title(f"Prediction: {prediction}")

classification_report erstellt einen Textbericht, der die wichtigsten Klassifizierungsmetriken anzeigt.

print(
    f"Classification report for classifier {clf}:\n"
    f"{metrics.classification_report(y_test, predicted)}\n"
)

Classification report for classifier SVC(gamma=0.001):
              precision    recall  f1-score   support

           0       1.00      0.99      0.99        88
           1       0.99      0.97      0.98        91
           2       0.99      0.99      0.99        86
           3       0.98      0.87      0.92        91
           4       0.99      0.96      0.97        92
           5       0.95      0.97      0.96        91
           6       0.99      0.99      0.99        91
           7       0.96      0.99      0.97        89
           8       0.94      1.00      0.97        88
           9       0.93      0.98      0.95        92

    accuracy                           0.97       899
   macro avg       0.97      0.97      0.97       899
weighted avg       0.97      0.97      0.97       899

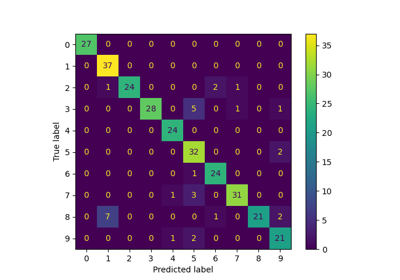
Wir können auch eine Konfusionsmatrix der wahren Ziffernwerte und der vorhergesagten Ziffernwerte plotten.

disp = metrics.ConfusionMatrixDisplay.from_predictions(y_test, predicted)
disp.figure_.suptitle("Confusion Matrix")
print(f"Confusion matrix:\n{disp.confusion_matrix}")

plt.show()

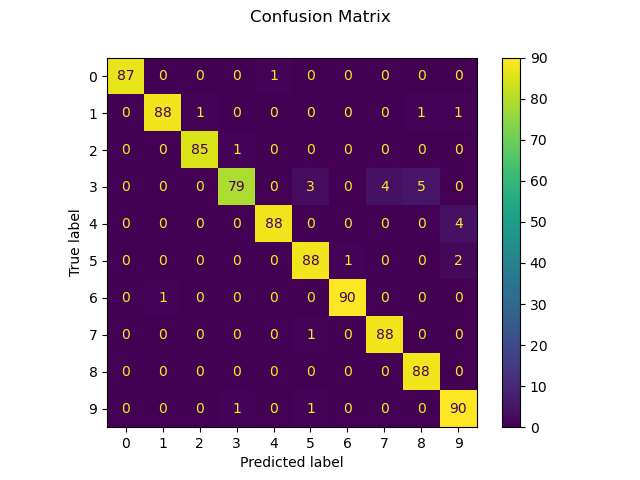
Confusion matrix:
[[87  0  0  0  1  0  0  0  0  0]
 [ 0 88  1  0  0  0  0  0  1  1]
 [ 0  0 85  1  0  0  0  0  0  0]
 [ 0  0  0 79  0  3  0  4  5  0]
 [ 0  0  0  0 88  0  0  0  0  4]
 [ 0  0  0  0  0 88  1  0  0  2]
 [ 0  1  0  0  0  0 90  0  0  0]
 [ 0  0  0  0  0  1  0 88  0  0]
 [ 0  0  0  0  0  0  0  0 88  0]
 [ 0  0  0  1  0  1  0  0  0 90]]

Wenn die Ergebnisse der Auswertung eines Klassifikators in Form einer Konfusionsmatrix und nicht in Form von y_true und y_pred gespeichert sind, kann man immer noch einen classification_report wie folgt erstellen

# The ground truth and predicted lists
y_true = []
y_pred = []
cm = disp.confusion_matrix

# For each cell in the confusion matrix, add the corresponding ground truths
# and predictions to the lists
for gt in range(len(cm)):
    for pred in range(len(cm)):
        y_true += [gt] * cm[gt][pred]
        y_pred += [pred] * cm[gt][pred]

print(
    "Classification report rebuilt from confusion matrix:\n"
    f"{metrics.classification_report(y_true, y_pred)}\n"
)

Classification report rebuilt from confusion matrix:
              precision    recall  f1-score   support

           0       1.00      0.99      0.99        88
           1       0.99      0.97      0.98        91
           2       0.99      0.99      0.99        86
           3       0.98      0.87      0.92        91
           4       0.99      0.96      0.97        92
           5       0.95      0.97      0.96        91
           6       0.99      0.99      0.99        91
           7       0.96      0.99      0.97        89
           8       0.94      1.00      0.97        88
           9       0.93      0.98      0.95        92

    accuracy                           0.97       899
   macro avg       0.97      0.97      0.97       899
weighted avg       0.97      0.97      0.97       899

Verwandte Beispiele

Merkmalsagglomeration

Merkmalsagglomeration

Label Propagation Ziffern: Leistung demonstrieren

Label Propagation Ziffern: Leistung demonstrieren

Label Propagation Ziffern: Aktives Lernen

Label Propagation Ziffern: Aktives Lernen

Bildrauschen mit Kernel PCA

Bildrauschen mit Kernel PCA