1.12. Multiklassen- und Multi-Output-Algorithmen#

Dieser Abschnitt des Benutzerhandbuchs behandelt Funktionalitäten im Zusammenhang mit Multi-Learning-Problemen, einschließlich Multiklassen-, Multilabel- und Multi-Output- Klassifizierung und Regression.

Die Module in diesem Abschnitt implementieren Meta-Estimators, die einen Basis-Estimator in ihrem Konstruktor benötigen. Meta-Estimators erweitern die Funktionalität des Basis-Estimators zur Unterstützung von Multi-Learning-Problemen, was durch die Umwandlung des Multi-Learning-Problems in eine Reihe einfacherer Probleme und anschließendes Anpassen eines Estimators pro Problem erreicht wird.

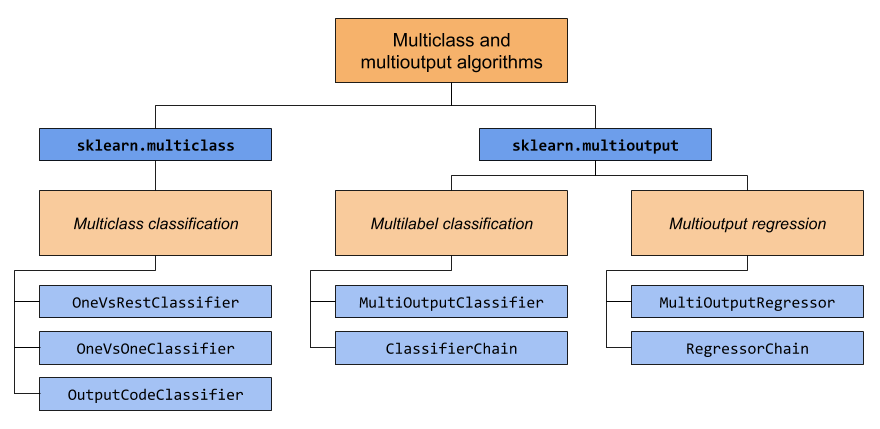
Dieser Abschnitt umfasst zwei Module: sklearn.multiclass und sklearn.multioutput. Die folgende Tabelle zeigt die Problemtypen, für die jedes Modul zuständig ist, und die entsprechenden Meta-Estimators, die jedes Modul bereitstellt.

../_images/multi_org_chart.png

Die folgende Tabelle bietet eine schnelle Referenz zu den Unterschieden zwischen den Problemtypen. Detailliertere Erklärungen finden Sie in den folgenden Abschnitten dieses Handbuchs.

Anzahl der Zielvariablen

Zielkardinalität

Gültiger type_of_target

Multiklassen-Klassifizierung

1

>2

„multiclass“

Multilabel-Klassifikation

>1

2 (0 oder 1)

„multilabel-indicator“

Multiklassen-Multi-Output-Klassifizierung

>1

>2

„multiclass-multioutput“

Multi-Output-Regression

>1

Kontinuierlich

„continuous-multioutput“

Im Folgenden finden Sie eine Zusammenfassung der scikit-learn-Estimators, die eine integrierte Multi-Learning-Unterstützung bieten, gruppiert nach Strategie. Sie benötigen die von diesem Abschnitt bereitgestellten Meta-Estimators nicht, wenn Sie einen dieser Estimators verwenden. Meta-Estimators können jedoch zusätzliche Strategien über die integrierten hinaus anbieten.

1.12.1. Multiklassen-Klassifizierung#

Warnung

Alle Klassifikatoren in scikit-learn können Multiklassen-Klassifizierung ohne zusätzlichen Aufwand durchführen. Sie müssen das Modul sklearn.multiclass nicht verwenden, es sei denn, Sie möchten verschiedene Multiklassen-Strategien ausprobieren.

Multiklassen-Klassifizierung ist eine Klassifizierungsaufgabe mit mehr als zwei Klassen. Jede Stichprobe kann nur einer Klasse zugeordnet werden.

Beispielsweise die Klassifizierung anhand von Merkmalen, die aus einer Reihe von Obstbildern extrahiert wurden, wobei jedes Bild entweder eine Orange, ein Apfel oder eine Birne sein kann. Jedes Bild ist eine Stichprobe und wird einer der 3 möglichen Klassen zugeordnet. Multiklassen-Klassifizierung geht davon aus, dass jeder Stichprobe genau ein Label zugewiesen wird – eine Stichprobe kann beispielsweise nicht gleichzeitig eine Birne und ein Apfel sein.

Obwohl alle scikit-learn-Klassifikatoren in der Lage sind, Multiklassen-Klassifizierung durchzuführen, ermöglichen die vom Modul sklearn.multiclass angebotenen Meta-Estimators die Änderung der Art und Weise, wie mehr als zwei Klassen behandelt werden, da dies die Leistung des Klassifikators beeinflussen kann (entweder in Bezug auf den Generalisierungsfehler oder die benötigten Rechenressourcen).

1.12.1.1. Zielformat#

Gültige Multiklassen- Darstellungen für type_of_target (y) sind:

  • 1D- oder Spaltenvektor mit mehr als zwei diskreten Werten. Ein Beispiel für einen Vektor y für 4 Stichproben.

    >>> import numpy as np
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> print(y)
['apple' 'pear' 'apple' 'orange']

  • Dichte oder spärliche binäre Matrix der Form (n_samples, n_classes) mit einer einzelnen Stichprobe pro Zeile, wobei jede Spalte eine Klasse darstellt. Ein Beispiel für eine dichte und eine spärliche binäre Matrix y für 4 Stichproben, wobei die Spalten in der Reihenfolge Apfel, Orange und Birne sind.

    >>> import numpy as np
>>> from sklearn.preprocessing import LabelBinarizer
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> y_dense = LabelBinarizer().fit_transform(y)
>>> print(y_dense)
[[1 0 0]
 [0 0 1]
 [1 0 0]
 [0 1 0]]
>>> from scipy import sparse
>>> y_sparse = sparse.csr_matrix(y_dense)
>>> print(y_sparse)
<Compressed Sparse Row sparse matrix of dtype 'int64'
  with 4 stored elements and shape (4, 3)>
  Coords Values
  (0, 0) 1
  (1, 2) 1
  (2, 0) 1
  (3, 1) 1

Weitere Informationen zu LabelBinarizer finden Sie unter Transformation des Vorhersageziels (y).

1.12.1.2. OneVsRestClassifier#

Die **One-vs-Rest**-Strategie, auch bekannt als **One-vs-All**, wird in OneVsRestClassifier implementiert. Die Strategie besteht darin, einen Klassifikator pro Klasse anzupassen. Für jeden Klassifikator wird die Klasse gegen alle anderen Klassen angepasst. Neben seiner rechnerischen Effizienz (nur n_classes Klassifikatoren sind erforderlich) ist ein Vorteil dieses Ansatzes seine Interpretierbarkeit. Da jede Klasse durch einen und nur einen Klassifikator repräsentiert wird, ist es möglich, Kenntnisse über die Klasse zu gewinnen, indem der entsprechende Klassifikator inspiziert wird. Dies ist die am häufigsten verwendete Strategie und eine faire Standardwahl.

Im Folgenden finden Sie ein Beispiel für Multiklassen-Lernen mit OvR.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

OneVsRestClassifier unterstützt auch Multilabel-Klassifizierung. Um diese Funktion zu nutzen, übergeben Sie dem Klassifikator eine Indikatormatrix, bei der Zelle [i, j] die Anwesenheit von Label j in Stichprobe i anzeigt.

../_images/sphx_glr_plot_multilabel_001.png

Beispiele

1.12.1.3. OneVsOneClassifier#

OneVsOneClassifier konstruiert einen Klassifikator pro Paar von Klassen. Bei der Vorhersage wird die Klasse ausgewählt, die die meisten Stimmen erhalten hat. Im Falle eines Gleichstands (zwischen zwei Klassen mit gleicher Stimmenzahl) wird die Klasse mit der höchsten aggregierten Klassifizierungskonfidenz ausgewählt, indem die paarweisen Klassifizierungskonfidenzniveaus, die von den zugrunde liegenden binären Klassifikatoren berechnet werden, summiert werden.

Da hierfür n_classes * (n_classes - 1) / 2 Klassifikatoren angepasst werden müssen, ist diese Methode aufgrund ihrer O(n_classes^2)-Komplexität in der Regel langsamer als One-vs-the-Rest. Diese Methode kann jedoch für Algorithmen wie Kernel-Algorithmen vorteilhaft sein, die nicht gut mit n_samples skalieren. Dies liegt daran, dass jedes einzelne Lernproblem nur eine kleine Teilmenge der Daten betrifft, während bei One-vs-the-Rest der vollständige Datensatz n_classes Mal verwendet wird. Die Entscheidungsfunktion ist das Ergebnis einer monotonen Transformation der Eins-gegen-Eins-Klassifizierung.

Im Folgenden finden Sie ein Beispiel für Multiklassen-Lernen mit OvO.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

Referenzen

  • „Pattern Recognition and Machine Learning. Springer“, Christopher M. Bishop, S. 183, (Erste Auflage)

1.12.1.4. OutputCodeClassifier#

Strategien, die auf fehlerkorrigierenden Ausgabe-Codes basieren, unterscheiden sich erheblich von One-vs-Rest und One-vs-One. Bei diesen Strategien wird jede Klasse in einem euklidischen Raum dargestellt, wobei jede Dimension nur 0 oder 1 sein kann. Anders ausgedrückt wird jede Klasse durch einen Binärcode (ein Array aus 0 und 1) repräsentiert. Die Matrix, die die Position/den Code jeder Klasse verfolgt, wird als Codebuch bezeichnet. Die Codegröße ist die Dimensionalität des oben genannten Raums. Intuitiv sollte jede Klasse durch einen möglichst eindeutigen Code repräsentiert werden, und ein gutes Codebuch sollte so gestaltet sein, dass die Klassifizierungsgenauigkeit optimiert wird. In dieser Implementierung verwenden wir einfach ein zufällig generiertes Codebuch, wie in [3] advocated, obwohl in Zukunft möglicherweise ausgefeiltere Methoden hinzugefügt werden.

Während des Anpassens wird ein binärer Klassifikator pro Bit im Codebuch angepasst. Bei der Vorhersage werden die Klassifikatoren verwendet, um neue Punkte in den Klassenraum zu projizieren, und die dem Punkt am nächsten liegende Klasse wird ausgewählt.

In OutputCodeClassifier ermöglicht das Attribut code_size dem Benutzer die Kontrolle über die Anzahl der zu verwendenden Klassifikatoren. Es ist ein Prozentsatz der Gesamtzahl der Klassen.

Eine Zahl zwischen 0 und 1 erfordert weniger Klassifikatoren als One-vs-Rest. Theoretisch reichen log2(n_classes) / n_classes aus, um jede Klasse eindeutig darzustellen. In der Praxis führt dies jedoch möglicherweise nicht zu einer guten Genauigkeit, da log2(n_classes) viel kleiner ist als n_classes.

Eine Zahl größer als 1 erfordert mehr Klassifikatoren als One-vs-Rest. In diesem Fall werden einige Klassifikatoren theoretisch Fehler korrigieren, die von anderen Klassifikatoren gemacht wurden, daher der Name "fehlerkorrigierend". In der Praxis kann dies jedoch nicht geschehen, da die Fehler von Klassifikatoren typischerweise korreliert sind. Die fehlerkorrigierenden Ausgabe-Codes haben eine ähnliche Wirkung wie Bagging.

Im Folgenden finden Sie ein Beispiel für Multiklassen-Lernen mit Ausgabe-Codes.

>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = OutputCodeClassifier(LinearSVC(random_state=0), code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

Referenzen

  • „Solving multiclass learning problems via error-correcting output codes“, Dietterich T., Bakiri G., Journal of Artificial Intelligence Research 2, 1995.

  • „The Elements of Statistical Learning“, Hastie T., Tibshirani R., Friedman J., S. 606 (zweite Auflage), 2008.

1.12.2. Multilabel-Klassifizierung#

Multilabel-Klassifizierung (eng verwandt mit **Multi-Output-Klassifizierung**) ist eine Klassifizierungsaufgabe, bei der jede Stichprobe mit m Labels aus n_classes möglichen Klassen versehen wird, wobei m von 0 bis n_classes reichen kann. Dies kann als Vorhersage von Eigenschaften einer Stichprobe betrachtet werden, die nicht gegenseitig ausschließend sind. Formal wird für jede Stichprobe eine binäre Ausgabe für jede Klasse zugewiesen. Positive Klassen werden mit 1 und negative Klassen mit 0 oder -1 angezeigt. Es ist somit vergleichbar mit der Durchführung von n_classes binären Klassifizierungsaufgaben, z. B. mit MultiOutputClassifier. Dieser Ansatz behandelt jedes Label unabhängig, während Multilabel-Klassifikatoren die mehreren Klassen *gleichzeitig* behandeln und korrelierte Verhaltensweisen unter ihnen berücksichtigen können.

Zum Beispiel die Vorhersage von Themen, die für ein Textdokument oder Video relevant sind. Das Dokument oder Video kann sich auf 'Religion', 'Politik', 'Finanzen' oder 'Bildung' beziehen, mehrere der Themenklassen oder alle Themenklassen.

1.12.2.1. Zielformat#

Eine gültige Darstellung von Multilabel- y ist eine dichte oder spärliche binäre Matrix der Form (n_samples, n_classes). Jede Spalte repräsentiert eine Klasse. Die 1en in jeder Zeile bezeichnen die positiven Klassen, mit denen eine Stichprobe gekennzeichnet wurde. Ein Beispiel für eine dichte Matrix y für 3 Stichproben.

>>> y = np.array([[1, 0, 0, 1], [0, 0, 1, 1], [0, 0, 0, 0]])
>>> print(y)
[[1 0 0 1]
 [0 0 1 1]
 [0 0 0 0]]

Dichte binäre Matrizen können auch mit MultiLabelBinarizer erstellt werden. Weitere Informationen finden Sie unter Transformation des Vorhersageziels (y).

Ein Beispiel für dieselbe y-Matrix in spärlicher Form.

>>> y_sparse = sparse.csr_matrix(y)
>>> print(y_sparse)
<Compressed Sparse Row sparse matrix of dtype 'int64'
  with 4 stored elements and shape (3, 4)>
  Coords Values
  (0, 0) 1
  (0, 3) 1
  (1, 2) 1
  (1, 3) 1

1.12.2.2. MultiOutputClassifier#

Die Unterstützung für Multilabel-Klassifizierung kann mit MultiOutputClassifier zu jedem Klassifikator hinzugefügt werden. Diese Strategie besteht darin, einen Klassifikator pro Zielvariable anzupassen. Dies ermöglicht Klassifizierungen mit mehreren Zielvariablen. Der Zweck dieser Klasse ist es, Estimators zu erweitern, um eine Reihe von Zielfunktionen (f1, f2, f3…, fn) schätzen zu können, die auf einer einzelnen X-Prädiktor-Matrix trainiert werden, um eine Reihe von Antworten (y1, y2, y3…, yn) vorherzusagen.

Ein Anwendungsbeispiel für MultiOutputClassifier finden Sie im Abschnitt über Multiklassen-Multi-Output-Klassifizierung, da es sich um eine Verallgemeinerung der Multilabel-Klassifizierung auf Multiklassen-Ausgaben anstelle von Binärausgaben handelt.

1.12.2.3. ClassifierChain#

Klassifikator-Ketten (siehe ClassifierChain) sind eine Möglichkeit, eine Anzahl von binären Klassifikatoren zu einem einzigen Multilabel-Modell zu kombinieren, das Korrelationen zwischen Zielvariablen nutzen kann.

Für ein Multilabel-Klassifizierungsproblem mit N Klassen werden N binäre Klassifikatoren einer ganzen Zahl zwischen 0 und N-1 zugeordnet. Diese ganzen Zahlen definieren die Reihenfolge der Modelle in der Kette. Jeder Klassifikator wird dann auf den verfügbaren Trainingsdaten plus den tatsächlichen Labels der Klassen angepasst, deren Modelle eine niedrigere Zahl zugewiesen wurde.

Bei der Vorhersage werden die tatsächlichen Labels nicht verfügbar sein. Stattdessen werden die Vorhersagen jedes Modells an die nachfolgenden Modelle in der Kette weitergegeben, um als Merkmale verwendet zu werden.

Offensichtlich ist die Reihenfolge der Kette wichtig. Das erste Modell in der Kette hat keine Informationen über die anderen Labels, während das letzte Modell in der Kette Merkmale aufweist, die die Anwesenheit aller anderen Labels anzeigen. Im Allgemeinen kennt man nicht die optimale Reihenfolge der Modelle in der Kette, daher werden typischerweise viele zufällig geordnete Ketten angepasst und ihre Vorhersagen werden gemittelt.

Referenzen

  • Jesse Read, Bernhard Pfahringer, Geoff Holmes, Eibe Frank, „Classifier Chains for Multi-label Classification“, 2009.

1.12.3. Multiklassen-Multi-Output-Klassifizierung#

Multiklassen-Multi-Output-Klassifizierung (auch als **Multitask-Klassifizierung** bekannt) ist eine Klassifizierungsaufgabe, die jede Stichprobe mit einer Menge von **nicht-binären** Eigenschaften kennzeichnet. Sowohl die Anzahl der Eigenschaften als auch die Anzahl der Klassen pro Eigenschaft ist größer als 2. Ein einzelner Estimator bearbeitet somit mehrere gemeinsame Klassifizierungsaufgaben. Dies ist sowohl eine Verallgemeinerung der Multi-**Label**-Klassifizierungsaufgabe, die nur binäre Attribute berücksichtigt, als auch eine Verallgemeinerung der Multi-**Klassen**-Klassifizierungsaufgabe, bei der nur eine Eigenschaft berücksichtigt wird.

Zum Beispiel die Klassifizierung der Eigenschaften "Obstsorte" und "Farbe" für eine Reihe von Obstbildern. Die Eigenschaft "Obstsorte" hat die möglichen Klassen: "Apfel", "Birne" und "Orange". Die Eigenschaft "Farbe" hat die möglichen Klassen: "grün", "rot", "gelb" und "orange". Jede Stichprobe ist ein Bild einer Frucht, für jede Eigenschaft wird ein Label ausgegeben, und jedes Label ist eine der möglichen Klassen der entsprechenden Eigenschaft.

Beachten Sie, dass alle Klassifikatoren, die Multiklassen-Multi-Output-Aufgaben (auch als Multitask-Klassifizierung bekannt) verarbeiten, die Multilabel-Klassifizierungsaufgabe als Sonderfall unterstützen. Multitask-Klassifizierung ist der Multi-Output-Klassifizierungsaufgabe mit unterschiedlichen Modellformulierungen ähnlich. Weitere Informationen finden Sie in der Dokumentation des entsprechenden Estimators.

Im Folgenden finden Sie ein Beispiel für Multiklassen-Multi-Output-Klassifizierung.

>>> from sklearn.datasets import make_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.utils import shuffle
>>> import numpy as np
>>> X, y1 = make_classification(n_samples=10, n_features=100,
...                             n_informative=30, n_classes=3,
...                             random_state=1)
>>> y2 = shuffle(y1, random_state=1)
>>> y3 = shuffle(y1, random_state=2)
>>> Y = np.vstack((y1, y2, y3)).T
>>> n_samples, n_features = X.shape # 10,100
>>> n_outputs = Y.shape[1] # 3
>>> n_classes = 3
>>> forest = RandomForestClassifier(random_state=1)
>>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=2)
>>> multi_target_forest.fit(X, Y).predict(X)
array([[2, 2, 0],
       [1, 2, 1],
       [2, 1, 0],
       [0, 0, 2],
       [0, 2, 1],
       [0, 0, 2],
       [1, 1, 0],
       [1, 1, 1],
       [0, 0, 2],
       [2, 0, 0]])

Warnung

Derzeit unterstützt keine Metrik in sklearn.metrics die Multiklassen-Multi-Output-Klassifizierungsaufgabe.

1.12.3.1. Zielformat#

Eine gültige Darstellung von Multi-Output- y ist eine dichte Matrix der Form (n_samples, n_classes) von Klassen-Labels. Eine spaltenweise Verkettung von 1D- Multiklassen- Variablen. Ein Beispiel für y für 3 Stichproben.

>>> y = np.array([['apple', 'green'], ['orange', 'orange'], ['pear', 'green']])
>>> print(y)
[['apple' 'green']
 ['orange' 'orange']
 ['pear' 'green']]

1.12.4. Multi-Output-Regression#

Multi-Output-Regression sagt mehrere numerische Eigenschaften für jede Stichprobe voraus. Jede Eigenschaft ist eine numerische Variable und die Anzahl der für jede Stichprobe vorherzusagenden Eigenschaften ist größer oder gleich 2. Einige Estimators, die Multi-Output-Regression unterstützen, sind schneller als die einfache Ausführung von n_output Estimators.

Zum Beispiel die Vorhersage von sowohl Windgeschwindigkeit als auch Windrichtung in Grad, unter Verwendung von Daten, die an einem bestimmten Ort gesammelt wurden. Jede Stichprobe wären Daten, die an einem Ort gesammelt wurden, und sowohl Windgeschwindigkeit als auch Richtung würden für jede Stichprobe ausgegeben.

Die folgenden Regressoren unterstützen nativ die Multi-Output-Regression:

1.12.4.1. Zielformat#

Eine gültige Darstellung von Multi-Output- y ist eine dichte Matrix der Form (n_samples, n_output) von Fließkommazahlen. Eine spaltenweise Verkettung von kontinuierlichen Variablen. Ein Beispiel für y für 3 Stichproben.

>>> y = np.array([[31.4, 94], [40.5, 109], [25.0, 30]])
>>> print(y)
[[ 31.4  94. ]
 [ 40.5 109. ]
 [ 25.   30. ]]

1.12.4.2. MultiOutputRegressor#

Die Unterstützung für Multi-Output-Regression kann mit MultiOutputRegressor zu jedem Regressor hinzugefügt werden. Diese Strategie besteht darin, einen Regressor pro Zielvariable anzupassen. Da jedes Ziel durch genau einen Regressor repräsentiert wird, ist es möglich, Kenntnisse über das Ziel zu gewinnen, indem der entsprechende Regressor inspiziert wird. Da MultiOutputRegressor einen Regressor pro Zielvariable anpasst, kann es keine Korrelationen zwischen Zielvariablen nutzen.

Im Folgenden finden Sie ein Beispiel für Multi-Output-Regression.

>>> from sklearn.datasets import make_regression
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1)
>>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X)
array([[-154.75474165, -147.03498585,  -50.03812219],
       [   7.12165031,    5.12914884,  -81.46081961],
       [-187.8948621 , -100.44373091,   13.88978285],
       [-141.62745778,   95.02891072, -191.48204257],
       [  97.03260883,  165.34867495,  139.52003279],
       [ 123.92529176,   21.25719016,   -7.84253   ],
       [-122.25193977,  -85.16443186, -107.12274212],
       [ -30.170388  ,  -94.80956739,   12.16979946],
       [ 140.72667194,  176.50941682,  -17.50447799],
       [ 149.37967282,  -81.15699552,   -5.72850319]])

1.12.4.3. RegressorChain#

Regressor-Ketten (siehe RegressorChain) sind analog zu ClassifierChain eine Methode, um eine Anzahl von Regressionen zu einem einzigen Multitarget-Modell zu kombinieren, das Korrelationen zwischen den Zielen nutzen kann.