1.17. Neuronale Netze (überwacht)#

Warnung

Diese Implementierung ist nicht für groß angelegte Anwendungen gedacht. Insbesondere bietet scikit-learn keine GPU-Unterstützung. Für deutlich schnellere, GPU-basierte Implementierungen sowie Frameworks, die mehr Flexibilität beim Aufbau von Deep-Learning-Architekturen bieten, siehe Verwandte Projekte.

1.17.1. Perzeptron mit mehreren Schichten#

Perzeptron mit mehreren Schichten (MLP) ist ein überwachter Lernalgorithmus, der eine Funktion \(f: R^m \rightarrow R^o\) lernt, indem er auf einem Datensatz trainiert wird, wobei \(m\) die Anzahl der Dimensionen für die Eingabe und \(o\) die Anzahl der Dimensionen für die Ausgabe ist. Gegeben eine Menge von Merkmalen \(X = \{x_1, x_2, ..., x_m\}\) und ein Ziel \(y\), kann es einen nichtlinearen Funktionsapproximator für Klassifizierung oder Regression lernen. Es unterscheidet sich von der logistischen Regression dadurch, dass sich zwischen der Eingabe- und der Ausgabeschicht eine oder mehrere nichtlineare Schichten befinden können, die als versteckte Schichten bezeichnet werden. Abbildung 1 zeigt ein MLP mit einer versteckten Schicht und skalarer Ausgabe.

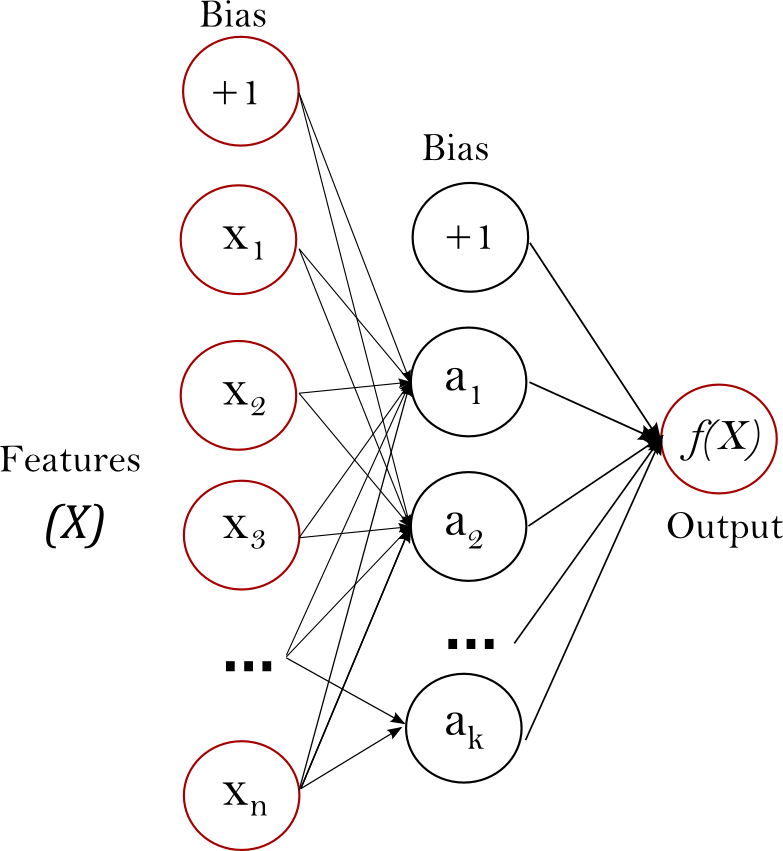
../_images/multilayerperceptron_network.png — **Abbildung 1: MLP mit einer versteckten Schicht.**#

Die äußerste linke Schicht, bekannt als Eingabeschicht, besteht aus einer Menge von Neuronen \(\{x_i | x_1, x_2, ..., x_m\}\), die die Eingabemerkmale darstellen. Jedes Neuron in der versteckten Schicht transformiert die Werte aus der vorherigen Schicht mit einer gewichteten linearen Summation \({w_1x_1 + w_2x_2 + ... + w_mx_m}\), gefolgt von einer nichtlinearen Aktivierungsfunktion \(g(\cdot):R \rightarrow R\) – wie der hyperbolische Tangens. Die Ausgabeschicht empfängt die Werte aus der letzten versteckten Schicht und transformiert sie in Ausgabewerte.

Das Modul enthält die öffentlichen Attribute coefs_ und intercepts_. coefs_ ist eine Liste von Gewichtsmatrizen, wobei die Gewichtsmatrix am Index \(i\) die Gewichte zwischen Schicht \(i\) und Schicht \(i+1\) darstellt. intercepts_ ist eine Liste von Bias-Vektoren, wobei der Vektor am Index \(i\) die Bias-Werte darstellt, die zur Schicht \(i+1\) addiert werden.

1.17.2. Klassifizierung#

Die Klasse MLPClassifier implementiert einen Multi-Layer Perceptron (MLP)-Algorithmus, der mithilfe von Backpropagation trainiert.

MLP trainiert auf zwei Arrays: Array X der Größe (n_samples, n_features), das die Trainingsstichproben als Gleitkomma-Merkmalsvektoren enthält; und Array y der Größe (n_samples,), das die Zielwerte (Klassenbezeichnungen) für die Trainingsstichproben enthält.

>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
              solver='lbfgs')

Nach dem Anpassen (Training) kann das Modell Bezeichnungen für neue Stichproben vorhersagen.

>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])

MLP kann ein nichtlineares Modell an die Trainingsdaten anpassen. clf.coefs_ enthält die Gewichtsmatrizen, die die Modellparameter bilden.

>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]

Derzeit unterstützt MLPClassifier nur die Kreuzentropie-Verlustfunktion, die Wahrscheinlichkeitsschätzungen durch Ausführung der Methode predict_proba ermöglicht.

MLP trainiert mithilfe von Backpropagation. Genauer gesagt, es trainiert mithilfe einer Form des Gradientenabstiegs und die Gradienten werden mithilfe von Backpropagation berechnet. Für die Klassifizierung minimiert es die Kreuzentropie-Verlustfunktion und liefert einen Vektor von Wahrscheinlichkeitsschätzungen \(P(y|x)\) pro Stichprobe \(x\).

>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967e-04, 9.998e-01],
       [1.967e-04, 9.998e-01]])

MLPClassifier unterstützt die multiklassen-Klassifizierung durch Anwendung von Softmax als Ausgabefunktion.

Darüber hinaus unterstützt das Modell die Multi-Label-Klassifizierung, bei der eine Stichprobe zu mehr als einer Klasse gehören kann. Für jede Klasse durchläuft die Rohausgabe die logistische Funktion. Werte größer oder gleich 0.5 werden auf 1 gerundet, andernfalls auf 0. Für eine vorhergesagte Ausgabe einer Stichprobe stellen die Indizes, bei denen der Wert 1 ist, die zugewiesenen Klassen dieser Stichprobe dar.

>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
              solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])

Siehe die folgenden Beispiele und die Docstring von MLPClassifier.fit für weitere Informationen.

Beispiele

Vergleich von stochastischen Lernstrategien für MLPClassifier
Siehe Visualisierung von MLP-Gewichten auf MNIST für eine visualisierte Darstellung von trainierten Gewichten.

1.17.3. Regression#

Die Klasse MLPRegressor implementiert ein Multi-Layer Perceptron (MLP), das mittels Backpropagation ohne Aktivierungsfunktion in der Ausgabeschicht trainiert, was auch als Verwendung der Identitätsfunktion als Aktivierungsfunktion betrachtet werden kann. Daher verwendet es den mittleren quadratischen Fehler als Verlustfunktion und die Ausgabe ist eine Menge kontinuierlicher Werte.

MLPRegressor unterstützt auch die Multi-Output-Regression, bei der eine Stichprobe mehr als ein Ziel haben kann.

1.17.4. Regularisierung#

Sowohl MLPRegressor als auch MLPClassifier verwenden den Parameter alpha für den Regularisierungs (L2-Regularisierung) Term, der zur Vermeidung von Überanpassung beiträgt, indem Gewichte mit großen Beträgen bestraft werden. Die folgende Abbildung zeigt die variierende Entscheidungsgrenze mit dem Wert von alpha.

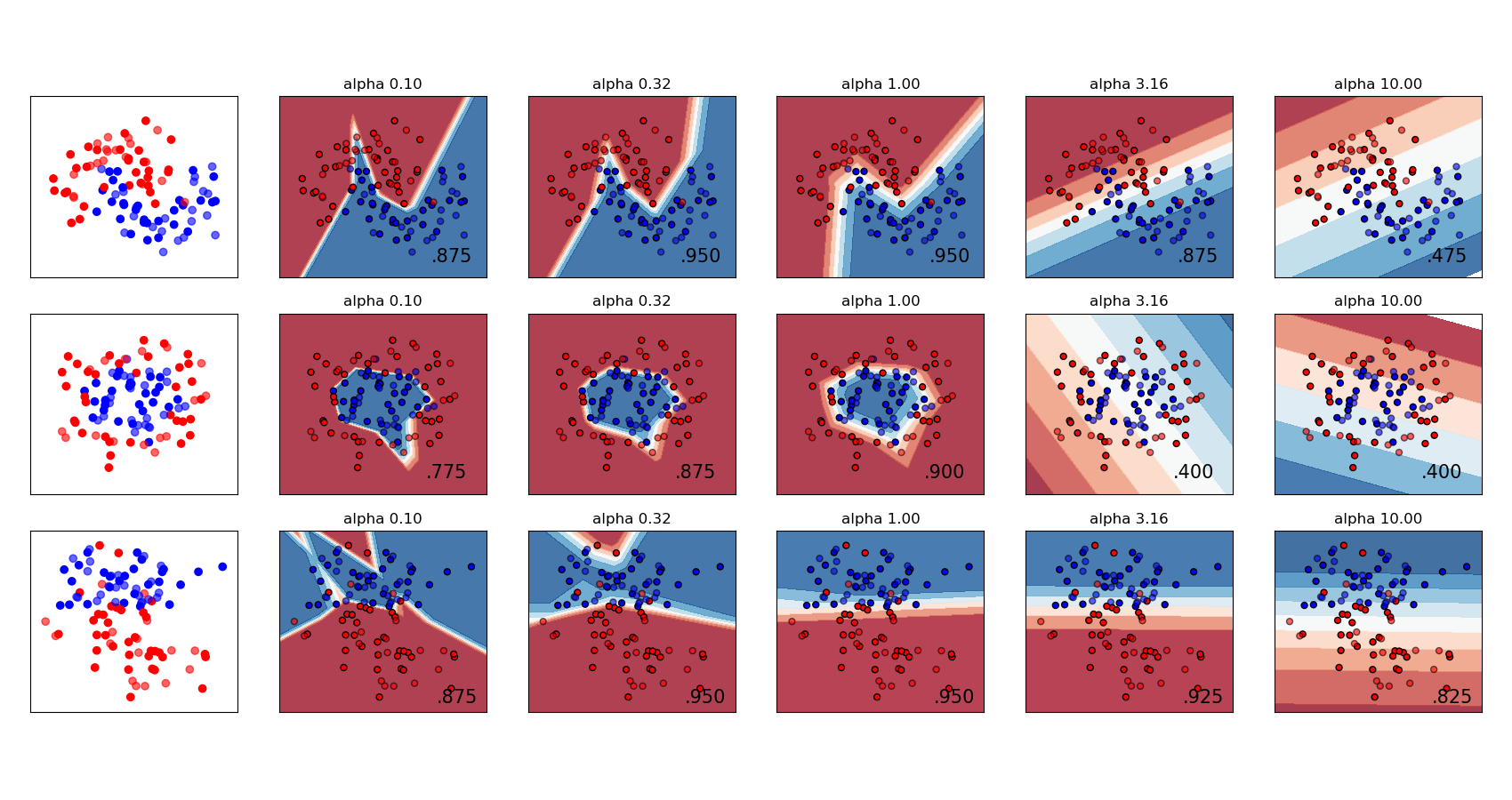
../_images/sphx_glr_plot_mlp_alpha_001.png

Siehe die folgenden Beispiele für weitere Informationen.

Beispiele

Variierende Regularisierung im Multi-Layer Perceptron

1.17.5. Algorithmen#

MLP trainiert mithilfe von stochastischem Gradientenabstieg, Adam oder L-BFGS. Stochastischer Gradientenabstieg (SGD) aktualisiert Parameter mithilfe des Gradienten der Verlustfunktion in Bezug auf einen anzupassenden Parameter, d.h.:

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial Loss}{\partial w}\right]\]

wobei \(\eta\) die Lernrate ist, die die Schrittgröße bei der Parametersuche steuert. \(Loss\) ist die für das Netzwerk verwendete Verlustfunktion.

Weitere Details finden Sie in der Dokumentation von SGD.

Adam ist ähnlich wie SGD insofern, als es ein stochastischer Optimierer ist, aber es kann die Aktualisierung von Parametern automatisch anpassen, basierend auf adaptiven Schätzungen niederer Ordnung von Momenten.

Mit SGD oder Adam unterstützt das Training Online- und Mini-Batch-Lernen.

L-BFGS ist ein Löser, der die Hesse-Matrix approximiert, die die partielle zweite Ableitung einer Funktion darstellt. Weiterhin approximiert er die Inverse der Hesse-Matrix zur Durchführung von Parameteraktualisierungen. Die Implementierung verwendet die Scipy-Version von L-BFGS.

Wenn der gewählte Löser 'L-BFGS' ist, unterstützt das Training weder Online- noch Mini-Batch-Lernen.

1.17.6. Komplexität#

Angenommen, es gibt \(n\) Trainingsstichproben, \(m\) Merkmale, \(k\) versteckte Schichten, die jeweils (der Einfachheit halber) \(h\) Neuronen enthalten, und \(o\) Ausgabeneuronen. Die Zeitkomplexität der Backpropagation beträgt \(O(i \cdot n \cdot (m \cdot h + (k - 1) \cdot h \cdot h + h \cdot o))\), wobei \(i\) die Anzahl der Iterationen ist. Da Backpropagation eine hohe Zeitkomplexität aufweist, ist es ratsam, mit einer geringeren Anzahl von versteckten Neuronen und wenigen versteckten Schichten für das Training zu beginnen.

Mathematische Formulierung#

Gegeben eine Menge von Trainingsbeispielen \(\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\), wobei \({x_i \in \mathbf{R}^n}\) und \({y_i \in \{0, 1\}}\), lernt ein MLP mit einer versteckten Schicht und einem versteckten Neuron die Funktion \(f(x) = W_2 g(W_1^T x + b_1) + b_2\), wobei \({W_1 \in \mathbf{R}^m}\) und \({W_2, b_1, b_2 \in \mathbf{R}}\) Modellparameter sind. \({W_1, W_2}\) repräsentieren die Gewichte der Eingabeschicht und der versteckten Schicht bzw.; und \({b_1, b_2}\) repräsentieren die Bias-Werte, die zur versteckten Schicht bzw. zur Ausgabeschicht addiert werden. \(g(\cdot) : R \rightarrow R\) ist die Aktivierungsfunktion, standardmäßig als hyperbolischer Tangens eingestellt. Sie ist wie folgt gegeben:

\[g(z)= \frac{e^z-e^{-z}}{e^z+e^{-z}}\]

Für binäre Klassifizierung durchläuft \(f(x)\) die logistische Funktion \(g(z)=1/(1+e^{-z})\), um Ausgabewerte zwischen Null und Eins zu erhalten. Ein Schwellenwert von 0,5 weist Stichproben mit Ausgaben größer oder gleich 0,5 der positiven Klasse und die restlichen der negativen Klasse zu.

Wenn es mehr als zwei Klassen gibt, ist \(f(x)\) selbst ein Vektor der Größe (n_classes,). Anstatt die logistische Funktion zu durchlaufen, durchläuft er die Softmax-Funktion, die wie folgt geschrieben wird:

\[\text{softmax}(z)_i = \frac{\exp(z_i)}{\sum_{l=1}^k\exp(z_l)}\]

wobei \({z_i}\) das \({i}\)-te Element der Eingabe für Softmax darstellt, das der Klasse \({i}\) entspricht, und \({K}\) die Anzahl der Klassen ist. Das Ergebnis ist ein Vektor, der die Wahrscheinlichkeiten enthält, dass die Stichprobe \({x}\) zu jeder Klasse gehört. Die Ausgabe ist die Klasse mit der höchsten Wahrscheinlichkeit.

Bei der Regression bleibt die Ausgabe \(f(x)\); daher ist die Ausgabefunktion einfach die Identitätsfunktion.

MLP verwendet je nach Problemtyp unterschiedliche Verlustfunktionen. Die Verlustfunktion für die Klassifizierung ist der durchschnittliche Kreuzentropieverlust, der im binären Fall wie folgt lautet:

\[Loss(\hat{y},y,W) = -\dfrac{1}{n}\sum_{i=0}^n(y_i \ln {\hat{y_i}} + (1-y_i) \ln{(1-\hat{y_i})}) + \dfrac{\alpha}{2n} ||W||_2^2\]

wobei \(\alpha ||W||_2^2\) ein L2-Regularisierungsterm (auch Penalty genannt) ist, der komplexe Modelle bestraft; und \(\alpha > 0\) ein nicht-negativer Hyperparameter ist, der die Stärke der Penalty steuert.

Für die Regression verwendet MLP die Verlustfunktion des mittleren quadratischen Fehlers; geschrieben als:

\[Loss(\hat{y},y,W) = \frac{1}{2n}\sum_{i=0}^n||\hat{y}_i - y_i ||_2^2 + \frac{\alpha}{2n} ||W||_2^2\]

Ausgehend von anfänglich zufälligen Gewichten minimiert das Multi-Layer Perceptron (MLP) die Verlustfunktion durch wiederholtes Aktualisieren dieser Gewichte. Nach der Berechnung des Verlusts wird dieser in einem Backward-Pass von der Ausgabeschicht zu den vorherigen Schichten propagiert, wodurch jeder Gewichtsparameter einen Update-Wert erhält, der den Verlust verringern soll.

Im Gradientenabstieg wird der Gradient \(\nabla Loss_{W}\) des Verlusts in Bezug auf die Gewichte berechnet und von \({W}\) abgezogen. Formeller wird dies wie folgt ausgedrückt:

\[W^{i+1} = W^i - \epsilon \nabla {Loss}_{W}^{i}\]

wobei \({i}\) der Iterationsschritt ist und \(\epsilon\) die Lernrate mit einem Wert größer als 0 ist.

Der Algorithmus stoppt, wenn er eine voreingestellte maximale Anzahl von Iterationen erreicht; oder wenn die Verbesserung des Verlusts unter einer bestimmten, kleinen Zahl liegt.

1.17.7. Tipps zur praktischen Anwendung#

Multi-Layer Perceptron ist empfindlich gegenüber Merkmalskalierung, daher wird dringend empfohlen, Ihre Daten zu skalieren. Skalieren Sie beispielsweise jedes Attribut im Eingangsvektor X auf [0, 1] oder [-1, +1], oder standardisieren Sie es so, dass es Mittelwert 0 und Varianz 1 hat. Beachten Sie, dass Sie dieselbe Skalierung auf den Testdatensatz anwenden müssen, um aussagekräftige Ergebnisse zu erzielen. Sie können StandardScaler zur Standardisierung verwenden.
```
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> # Don't cheat - fit only on training data
>>> scaler.fit(X_train)
>>> X_train = scaler.transform(X_train)
>>> # apply same transformation to test data
>>> X_test = scaler.transform(X_test)
```
Ein alternativer und empfohlener Ansatz ist die Verwendung von StandardScaler in einer Pipeline.
Das Finden eines sinnvollen Regularisierungsparameters \(\alpha\) ist am besten mit GridSearchCV zu tun, normalerweise im Bereich von 10.0 ** -np.arange(1, 7).
Empirisch haben wir beobachtet, dass L-BFGS bei kleinen Datensätzen schneller und mit besseren Lösungen konvergiert. Für relativ große Datensätze ist Adam jedoch sehr robust. Es konvergiert normalerweise schnell und liefert ziemlich gute Leistungen. SGD mit Momentum oder Nesterov-Momentum kann dagegen besser als diese beiden Algorithmen abschneiden, wenn die Lernrate korrekt eingestellt ist.

1.17.8. Mehr Kontrolle mit warm_start#

Wenn Sie mehr Kontrolle über Stoppkriterien oder die Lernrate in SGD wünschen oder zusätzliche Überwachung durchführen möchten, kann die Verwendung von warm_start=True und max_iter=1 und anschließendes eigenes Iterieren hilfreich sein.

>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
...     clf.fit(X, y)
...     # additional monitoring / inspection
MLPClassifier(...