3.1. Kreuzvalidierung: Evaluierung der Modellleistung

Das Erlernen der Parameter einer Vorhersagefunktion und deren Testen an denselben Daten ist ein methodischer Fehler: Ein Modell, das einfach die Labels der gerade gesehenen Samples wiederholen würde, hätte eine perfekte Punktzahl, würde aber nichts Nützliches für noch ungesehene Daten vorhersagen. Diese Situation wird als Überanpassung (overfitting) bezeichnet. Um dies zu vermeiden, ist es übliche Praxis bei einem (überwachten) maschinellen Lernexperiment, einen Teil der verfügbaren Daten als Testset X_test, y_test zurückzuhalten. Beachten Sie, dass das Wort "Experiment" nicht nur für den akademischen Gebrauch bestimmt ist, da selbst in kommerziellen Umgebungen maschinelles Lernen normalerweise experimentell beginnt. Hier ist ein Flussdiagramm des typischen Kreuzvalidierungs-Workflows im Modelltraining. Die besten Parameter können durch Grid-Search-Techniken bestimmt werden.

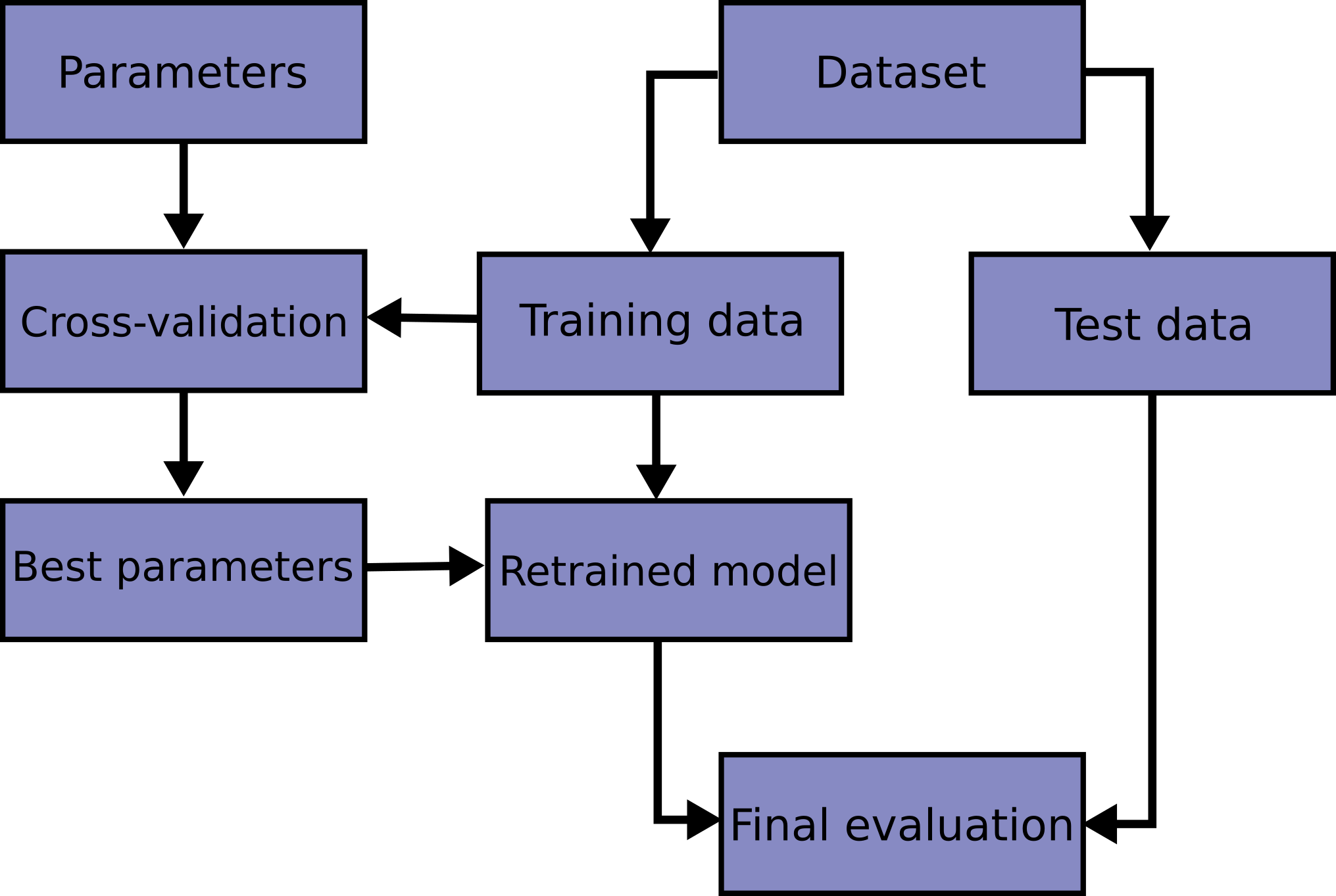
In scikit-learn kann eine zufällige Aufteilung in Trainings- und Testsets schnell mit der Hilfsfunktion train_test_split berechnet werden. Laden wir den Iris-Datensatz, um darauf einen linearen Support Vector Machine anzupassen.

>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm

>>> X, y = datasets.load_iris(return_X_y=True)
>>> X.shape, y.shape
((150, 4), (150,))

Wir können nun schnell ein Trainingsset sampeln und gleichzeitig 40% der Daten für das Testen (Evaluieren) unseres Klassifikators zurückhalten.

>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)

>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))

>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96

Bei der Evaluierung verschiedener Einstellungen ("Hyperparameter") für Modelle, wie z. B. die Einstellung C, die für einen SVM manuell festgelegt werden muss, besteht weiterhin die Gefahr der Überanpassung auf dem Testset, da die Parameter so lange angepasst werden können, bis das Modell optimal leistet. Auf diese Weise kann Wissen über das Testset in das Modell "sickern", und die Evaluationsmetriken berichten nicht mehr über die Generalisierungsleistung. Um dieses Problem zu lösen, kann ein weiterer Teil des Datensatzes als sogenanntes "Validierungsset" zurückgehalten werden: Das Training erfolgt auf dem Trainingsset, danach erfolgt die Evaluation auf dem Validierungsset, und wenn das Experiment erfolgreich zu sein scheint, kann die finale Evaluation auf dem Testset erfolgen.

Durch die Aufteilung der verfügbaren Daten in drei Sets reduzieren wir jedoch drastisch die Anzahl der Samples, die zum Erlernen des Modells verwendet werden können, und die Ergebnisse können von einer bestimmten zufälligen Wahl des (Trainings-, Validierungs-) Paares abhängen.

Eine Lösung für dieses Problem ist ein Verfahren namens Kreuzvalidierung (kurz CV). Ein Testset sollte immer noch für die finale Evaluation zurückgehalten werden, aber das Validierungsset wird bei der CV nicht mehr benötigt. Im grundlegenden Ansatz, der sogenannten k-fachen CV, wird das Trainingsset in k kleinere Mengen aufgeteilt (andere Ansätze werden unten beschrieben, folgen aber generell denselben Prinzipien). Das folgende Verfahren wird für jede der k "Folds" befolgt:

• Ein Modell wird trainiert, indem \(k-1\) der Folds als Trainingsdaten verwendet werden;

• das resultierende Modell wird auf dem verbleibenden Teil der Daten validiert (d. h. es wird als Testset verwendet, um eine Leistungskennzahl wie die Genauigkeit zu berechnen).

Die von der k-fachen Kreuzvalidierung berichtete Leistungskennzahl ist dann der Durchschnitt der im Loop berechneten Werte. Dieser Ansatz kann rechenintensiv sein, verschwendet aber nicht zu viele Daten (wie es bei der Festlegung eines beliebigen Validierungssets der Fall ist), was ein großer Vorteil bei Problemen wie der inversen Inferenz ist, bei denen die Anzahl der Samples sehr gering ist.

3.1.1. Berechnung kreuzvalidierter Metriken

Der einfachste Weg, Kreuzvalidierung zu nutzen, ist der Aufruf der Hilfsfunktion cross_val_score auf das Modell und den Datensatz.

Das folgende Beispiel zeigt, wie die Genauigkeit eines linearen Kernel-Support-Vector-Machines auf dem Iris-Datensatz geschätzt werden kann, indem die Daten aufgeteilt, ein Modell angepasst und die Punktzahl 5 Mal hintereinander berechnet wird (jedes Mal mit anderen Aufteilungen).

>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1, random_state=42)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores
array([0.96, 1. , 0.96, 0.96, 1. ])

Der mittlere Score und die Standardabweichung ergeben sich somit aus

>>> print("%0.2f accuracy with a standard deviation of %0.2f" % (scores.mean(), scores.std()))
0.98 accuracy with a standard deviation of 0.02

Standardmäßig ist der Score, der bei jeder CV-Iteration berechnet wird, die score-Methode des Modells. Dies kann durch Verwendung des `scoring`-Parameters geändert werden.

>>> from sklearn import metrics
>>> scores = cross_val_score(
...     clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96, 1., 0.96, 0.96, 1.])

Siehe Der Scoring-Parameter: Regeln zur Modellbewertung definieren für Details. Im Fall des Iris-Datensatzes sind die Samples über die Zielklassen ausgeglichen, daher sind die Genauigkeit und der F1-Score fast gleich.

Wenn das Argument cv eine Ganzzahl ist, verwendet cross_val_score standardmäßig die Strategien KFold oder StratifiedKFold, wobei letztere verwendet wird, wenn das Modell von ClassifierMixin abgeleitet ist.

Es ist auch möglich, andere Kreuzvalidierungsstrategien zu verwenden, indem stattdessen ein Kreuzvalidierungs-Iterator übergeben wird, zum Beispiel

>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977, 0.977, 1., 0.955, 1.])

Eine andere Option ist die Verwendung eines Iterables, das (Trainings-, Test-) Splits als Indizes liefert, zum Beispiel

>>> def custom_cv_2folds(X):
...     n = X.shape[0]
...     i = 1
...     while i <= 2:
...         idx = np.arange(n * (i - 1) / 2, n * i / 2, dtype=int)
...         yield idx, idx
...         i += 1
...
>>> custom_cv = custom_cv_2folds(X)
>>> cross_val_score(clf, X, y, cv=custom_cv)
array([1.        , 0.973])

Datentransformation mit zurückgehaltenen Daten

Genauso wie es wichtig ist, einen Prädiktor auf Daten zu testen, die vom Training zurückgehalten wurden, sollten Vorverarbeitungsschritte (wie Standardisierung, Merkmalsauswahl usw.) und ähnliche Datentransformationen ebenfalls aus einem Trainingsset gelernt und für Vorhersagen auf zurückgehaltenen Daten angewendet werden.

>>> from sklearn import preprocessing
>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> X_train_transformed = scaler.transform(X_train)
>>> clf = svm.SVC(C=1).fit(X_train_transformed, y_train)
>>> X_test_transformed = scaler.transform(X_test)
>>> clf.score(X_test_transformed, y_test)
0.9333

Eine Pipeline erleichtert die Kombination von Modellen und bietet dieses Verhalten unter Kreuzvalidierung.

>>> from sklearn.pipeline import make_pipeline
>>> clf = make_pipeline(preprocessing.StandardScaler(), svm.SVC(C=1))
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977, 0.933, 0.955, 0.933, 0.977])

Siehe Pipelines und zusammengesetzte Modelle.

3.1.1.1. Die Funktion `cross_validate` und die Bewertung mehrerer Metriken

Die Funktion cross_validate unterscheidet sich von cross_val_score in zweierlei Hinsicht:

• Sie ermöglicht die Angabe mehrerer Metriken für die Bewertung.

• Sie gibt zusätzlich zum Test-Score ein Dict zurück, das Trainingszeiten, Score-Zeiten (und optional Trainings-Scores, angepasste Modelle, Trainings-Test-Split-Indizes) enthält.

Bei der Bewertung einer einzelnen Metrik, bei der der `scoring`-Parameter ein String, aufrufbar oder `None` ist, sind die Schlüssel - ['test_score', 'fit_time', 'score_time']

Und bei der Bewertung mehrerer Metriken ist der Rückgabewert ein Dict mit den folgenden Schlüsseln - ['test_<scorer1_name>', 'test_<scorer2_name>', 'test_<scorer...>', 'fit_time', 'score_time']

return_train_score ist standardmäßig auf False gesetzt, um Rechenzeit zu sparen. Um die Scores auch auf dem Trainingsset zu evaluieren, müssen Sie ihn auf True setzen. Sie können auch das auf jedem Trainingsset angepasste Modell beibehalten, indem Sie return_estimator=True setzen. Ebenso können Sie return_indices=True setzen, um die Trainings- und Testindizes zu erhalten, die für die Aufteilung des Datensatzes in Trainings- und Testsets für jeden CV-Split verwendet wurden.

Die multiplen Metriken können entweder als Liste, Tupel oder Menge vordefinierter Score-Namen angegeben werden.

>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96, 1., 0.96, 0.96, 1.])

Oder als Dict, das den Score-Namen auf eine vordefinierte oder benutzerdefinierte Scoring-Funktion abbildet.

>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
...            'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
...                         cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
 'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
array([0.97, 0.97, 0.99, 0.98, 0.98])

Hier ist ein Beispiel für cross_validate, das eine einzelne Metrik verwendet.

>>> scores = cross_validate(clf, X, y,
...                         scoring='precision_macro', cv=5,
...                         return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']

3.1.1.2. Vorhersagen durch Kreuzvalidierung erhalten

Die Funktion cross_val_predict hat eine ähnliche Schnittstelle wie cross_val_score, gibt aber für jedes Element der Eingabe die Vorhersage zurück, die für dieses Element erhalten wurde, als es sich im Testset befand. Nur Kreuzvalidierungsstrategien, die alle Elemente genau einmal einem Testset zuweisen, können verwendet werden (andernfalls wird eine Ausnahme ausgelöst).

Warnung

Hinweis zur unangemessenen Verwendung von `cross_val_predict`

Das Ergebnis von cross_val_predict kann sich von dem mit cross_val_score erhaltenen unterscheiden, da die Elemente unterschiedlich gruppiert sind. Die Funktion cross_val_score mittelt über Kreuzvalidierungs-Folds, während cross_val_predict einfach die Labels (oder Wahrscheinlichkeiten) aus mehreren unterschiedlichen Modellen unverändert zurückgibt. Daher ist cross_val_predict keine geeignete Maßzahl für den Generalisierungsfehler.

Die Funktion cross_val_predict ist geeignet für:

• Visualisierung von Vorhersagen, die von verschiedenen Modellen erhalten wurden.

• Modell-Blending: Wenn Vorhersagen eines überwachten Modells zum Trainieren eines anderen Modells in Ensemble-Methoden verwendet werden.

Die verfügbaren Kreuzvalidierungs-Iteratoren werden im folgenden Abschnitt vorgestellt.

Beispiele

• Receiver Operating Characteristic (ROC) mit Kreuzvalidierung,

• Rekursive Merkmalseliminierung mit Kreuzvalidierung,

• Benutzerdefinierte Refit-Strategie einer Gitter-Suche mit Kreuzvalidierung,

• Beispiel-Pipeline für Textmerkmal-Extraktion und -Bewertung,

• Kreuzvalidierte Vorhersagen plotten,

• Verschachtelte vs. nicht verschachtelte Kreuzvalidierung.

3.1.2. Kreuzvalidierungs-Iteratoren

Die folgenden Abschnitte listen Dienstprogramme zur Generierung von Indizes auf, die zur Erzeugung von Datensatzaufteilungen gemäß verschiedenen Kreuzvalidierungsstrategien verwendet werden können.

3.1.2.1. Kreuzvalidierungs-Iteratoren für i.i.d.-Daten

Die Annahme, dass Daten unabhängig und identisch verteilt (i.i.d.) sind, bedeutet, dass alle Samples aus demselben generativen Prozess stammen und angenommen wird, dass der generative Prozess keine Erinnerung an bisher generierte Samples hat.

Die folgenden Kreuzvalidatoren können in solchen Fällen verwendet werden.

Hinweis

Während i.i.d.-Daten eine gängige Annahme in der Theorie des maschinellen Lernens sind, trifft dies in der Praxis selten zu. Wenn bekannt ist, dass die Samples mittels eines zeitabhängigen Prozesses generiert wurden, ist es sicherer, ein zeitreihenbewusstes Kreuzvalidierungsschema zu verwenden. Ebenso, wenn bekannt ist, dass der generative Prozess eine Gruppenstruktur aufweist (Samples von verschiedenen Subjekten, Experimenten, Messgeräten gesammelt), ist es sicherer, eine gruppenweise Kreuzvalidierung zu verwenden.

3.1.2.1.1. K-Fold

KFold teilt alle Samples in \(k\) Gruppen von Samples, genannt Folds (wenn \(k = n\), ist dies äquivalent zur Leave One Out Strategie), gleicher Größe (wenn möglich). Die Vorhersagefunktion wird unter Verwendung von \(k - 1\) Folds gelernt, und der ausgelassene Fold wird für den Test verwendet.

Beispiel für 2-fache Kreuzvalidierung auf einem Datensatz mit 4 Samples

>>> import numpy as np
>>> from sklearn.model_selection import KFold

>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens. Beachten Sie, dass KFold nicht von Klassen oder Gruppen beeinflusst wird.

Jeder Fold besteht aus zwei Arrays: das erste bezieht sich auf das Trainingsset, das zweite auf das Testset. Daher kann man die Trainings-/Testsets mithilfe von Numpy-Indizierung erstellen.

>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> y = np.array([0, 1, 0, 1])
>>> X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]

3.1.2.1.2. Wiederholtes K-Fold

RepeatedKFold wiederholt KFold \(n\) Mal und erzeugt dabei unterschiedliche Splits bei jeder Wiederholung.

Beispiel für 2-faches K-Fold, wiederholt 2 Mal.

>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
...     print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]

Ähnlich wiederholt RepeatedStratifiedKFold StratifiedKFold \(n\) Mal mit unterschiedlicher Zufälligkeit bei jeder Wiederholung.

3.1.2.1.3. Leave One Out (LOO)

LeaveOneOut (oder LOO) ist eine einfache Kreuzvalidierung. Jedes Lernset wird erstellt, indem alle Samples bis auf eines genommen werden, wobei das Testset das ausgelassene Sample ist. Für \(n\) Samples haben wir also \(n\) verschiedene Trainingssets und \(n\) verschiedene Testsets. Dieses Kreuzvalidierungsverfahren verschwendet nicht viel Daten, da nur ein Sample vom Trainingsset entfernt wird.

>>> from sklearn.model_selection import LeaveOneOut

>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
...     print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

Potenzielle Anwender von LOO für die Modellauswahl sollten einige bekannte Einschränkungen abwägen. Im Vergleich zur k-fachen Kreuzvalidierung werden \(n\) Modelle aus \(n\) Samples anstelle von \(k\) Modellen aufgebaut, wobei \(n > k\) ist. Außerdem werden sie auf \(n - 1\) Samples trainiert anstatt auf \((k-1) n / k\). In beiden Fällen ist LOO, unter der Annahme, dass \(k\) nicht zu groß und \(k < n\) ist, rechenintensiver als die k-fache Kreuzvalidierung.

In Bezug auf die Genauigkeit führt LOO oft zu einer hohen Varianz als Schätzer für den Testfehler. Intuitiv, da \(n - 1\) der \(n\) Samples zum Aufbau jedes Modells verwendet werden, sind die aus den Folds konstruierten Modelle nahezu identisch zueinander und zum Modell, das aus dem gesamten Trainingsset aufgebaut wurde.

Wenn jedoch die Lernkurve für die betrachtete Trainingsgröße steil ist, können 5- oder 10-fache Kreuzvalidierung den Generalisierungsfehler überschätzen.

Als allgemeine Regel empfehlen die meisten Autoren und empirischen Belege, dass 5- oder 10-fache Kreuzvalidierung LOO vorgezogen werden sollte.

Referenzen

• http://www.faqs.org/faqs/ai-faq/neural-nets/part3/section-12.html;

• T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer 2009

• L. Breiman, P. Spector Submodel selection and evaluation in regression: The X-random case, International Statistical Review 1992;

• R. Kohavi, A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection, Intl. Jnt. Conf. AI

• R. Bharat Rao, G. Fung, R. Rosales, On the Dangers of Cross-Validation. An Experimental Evaluation, SIAM 2008;

• G. James, D. Witten, T. Hastie, R. Tibshirani, An Introduction to Statistical Learning, Springer 2013.

3.1.2.1.4. Leave P Out (LPO)

LeavePOut ist sehr ähnlich zu LeaveOneOut, da es alle möglichen Trainings-/Testsets erstellt, indem \(p\) Samples aus dem vollständigen Set entfernt werden. Für \(n\) Samples erzeugt dies \({n \choose p}\) Trainings-Test-Paare. Im Gegensatz zu LeaveOneOut und KFold werden sich die Testsets für \(p > 1\) überlappen.

Beispiel für Leave-2-Out auf einem Datensatz mit 4 Samples

>>> from sklearn.model_selection import LeavePOut

>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]

3.1.2.1.5. Zufällige Permutationen Kreuzvalidierung a.k.a. Shuffle & Split

Der Iterator ShuffleSplit generiert eine benutzerdefinierte Anzahl von unabhängigen Trainings-/Testdatensatz-Splits. Die Samples werden zuerst gemischt und dann in ein Paar von Trainings- und Testsets aufgeteilt.

Es ist möglich, die Zufälligkeit für die Reproduzierbarkeit der Ergebnisse zu steuern, indem der Pseudo-Zufallszahlengenerator `random_state` explizit gesetzt wird.

Hier ist ein Anwendungsbeispiel.

>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.arange(10)
>>> ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
>>> for train_index, test_index in ss.split(X):
...     print("%s %s" % (train_index, test_index))
[9 1 6 7 3 0 5] [2 8 4]
[2 9 8 0 6 7 4] [3 5 1]
[4 5 1 0 6 9 7] [2 3 8]
[2 7 5 8 0 3 4] [6 1 9]
[4 1 0 6 8 9 3] [5 2 7]

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens. Beachten Sie, dass ShuffleSplit nicht von Klassen oder Gruppen beeinflusst wird.

ShuffleSplit ist somit eine gute Alternative zur KFold-Kreuzvalidierung, die eine feinere Kontrolle über die Anzahl der Iterationen und den Anteil der Samples auf jeder Seite des Trainings-/Test-Splits ermöglicht.

3.1.2.2. Kreuzvalidierungs-Iteratoren mit Stratifizierung basierend auf Klassenlabels

Einige Klassifizierungsaufgaben können von Natur aus seltene Klassen aufweisen: zum Beispiel könnten viel mehr negative Beobachtungen als positive Beobachtungen vorhanden sein (z. B. medizinische Screening, Betrugserkennung usw.). Folglich können Kreuzvalidierungs-Splits Trainings- oder Validierungs-Folds ohne jegliches Vorkommen einer bestimmten Klasse generieren. Dies führt typischerweise zu undefinierten Klassifizierungsmetriken (z. B. ROC AUC), Ausnahmen beim Versuch, fit aufzurufen, oder fehlenden Spalten in der Ausgabe der Methoden predict_proba oder decision_function von Multiklassen-Klassifikatoren, die auf verschiedenen Folds trainiert wurden.

Um solche Probleme zu mildern, implementieren Splitter wie StratifiedKFold und StratifiedShuffleSplit stratifizierte Stichproben, um sicherzustellen, dass die relativen Klassenverhältnisse in jedem Fold annähernd erhalten bleiben.

Hinweis

Die stratifizierte Stichprobenentnahme wurde in scikit-learn eingeführt, um die oben genannten technischen Probleme zu umgehen und nicht um statistische zu lösen.

Die Stratifizierung macht Kreuzvalidierungs-Folds homogener und verbirgt infolgedessen einige der Variabilität, die bei der Anpassung von Modellen mit einer begrenzten Anzahl von Beobachtungen inhärent ist.

Infolgedessen kann die Stratifizierung die Streuung der über die Kreuzvalidierungs-Iterationen gemessenen Metrik künstlich verringern: Die Inter-Fold-Variabilität spiegelt nicht mehr die Unsicherheit der Modellleistung angesichts seltener Klassen wider.

3.1.2.2.1. Stratified K-fold

StratifiedKFold ist eine Variante von K-fold, die stratifizierte Folds liefert: Jedes Set enthält ungefähr den gleichen Prozentsatz an Samples jeder Zielklasse wie das vollständige Set.

Hier ist ein Beispiel für stratifizierte 3-fache Kreuzvalidierung auf einem Datensatz mit 50 Samples aus zwei unausgeglichenen Klassen. Wir zeigen die Anzahl der Samples in jeder Klasse und vergleichen sie mit KFold.

>>> from sklearn.model_selection import StratifiedKFold, KFold
>>> import numpy as np
>>> X, y = np.ones((50, 1)), np.hstack(([0] * 45, [1] * 5))
>>> skf = StratifiedKFold(n_splits=3)
>>> for train, test in skf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [30  3]   |   test -  [15  2]
train -  [30  3]   |   test -  [15  2]
train -  [30  4]   |   test -  [15  1]
>>> kf = KFold(n_splits=3)
>>> for train, test in kf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [28  5]   |   test -  [17]
train -  [28  5]   |   test -  [17]
train -  [34]   |   test -  [11  5]

Wir sehen, dass StratifiedKFold die Klassenverhältnisse (ungefähr 1 / 10) sowohl in den Trainings- als auch in den Testdatensätzen beibehält.

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens.

RepeatedStratifiedKFold kann verwendet werden, um Stratified K-Fold n Mal mit unterschiedlicher Zufälligkeit bei jeder Wiederholung zu wiederholen.

3.1.2.2.2. Stratified Shuffle Split

StratifiedShuffleSplit ist eine Variante von ShuffleSplit, die stratifizierte Splits liefert, d. h., die Splits durch Beibehaltung desselben Prozentsatzes für jede Zielklasse wie im vollständigen Set erstellt.

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens.

3.1.2.3. Vordefinierte Fold-Splits / Validierungs-Sets

Für einige Datensätze existiert bereits eine vordefinierte Aufteilung der Daten in Trainings- und Validierungs-Folds oder in mehrere Kreuzvalidierungs-Folds. Mit PredefinedSplit ist es möglich, diese Folds zu verwenden, z. B. bei der Suche nach Hyperparametern.

Zum Beispiel, wenn ein Validierungsset verwendet wird, setzen Sie den test_fold auf 0 für alle Samples, die Teil des Validierungssets sind, und auf -1 für alle anderen Samples.

3.1.2.4. Kreuzvalidierungs-Iteratoren für gruppierte Daten

Die i.i.d.-Annahme ist ungültig, wenn der zugrundeliegende generative Prozess Gruppen abhängiger Samples liefert.

Eine solche Gruppierung von Daten ist domänenspezifisch. Ein Beispiel wäre, wenn medizinische Daten von mehreren Patienten gesammelt wurden, wobei von jedem Patienten mehrere Samples entnommen wurden. Und solche Daten sind wahrscheinlich abhängig von der individuellen Gruppe. In unserem Beispiel ist die Patienten-ID für jedes Sample sein Gruppenidentifikator.

In diesem Fall möchten wir wissen, ob ein Modell, das auf einer bestimmten Gruppe von Gruppen trainiert wurde, gut auf die unbekannten Gruppen generalisiert. Um dies zu messen, müssen wir sicherstellen, dass alle Samples im Validierungs-Fold aus Gruppen stammen, die im zugehörigen Trainings-Fold überhaupt nicht vertreten sind.

Die folgenden Kreuzvalidierungs-Splitter können dafür verwendet werden. Der Gruppierungsidentifikator für die Samples wird über den Parameter groups spezifiziert.

3.1.2.4.1. Group K-fold

GroupKFold ist eine Variante von K-fold, die sicherstellt, dass dieselbe Gruppe nicht sowohl im Test- als auch im Trainingssatz vertreten ist. Zum Beispiel, wenn die Daten von verschiedenen Subjekten mit mehreren Samples pro Subjekt stammen und das Modell flexibel genug ist, um aus stark personenspezifischen Merkmalen zu lernen, könnte es bei neuen Subjekten versagen zu generalisieren. GroupKFold ermöglicht es, diese Art von Überanpassungssituationen zu erkennen.

Stellen Sie sich drei Subjekte vor, denen jeweils eine Zahl von 1 bis 3 zugeordnet ist.

>>> from sklearn.model_selection import GroupKFold

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
>>> groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

>>> gkf = GroupKFold(n_splits=3)
>>> for train, test in gkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]

Jedes Subjekt befindet sich in einem anderen Test-Fold, und dasselbe Subjekt ist niemals sowohl im Test- als auch im Training enthalten. Beachten Sie, dass die Folds aufgrund der unausgeglichenen Daten nicht genau die gleiche Größe haben. Wenn Klassenproportionen über die Folds ausgeglichen werden müssen, ist StratifiedGroupKFold eine bessere Option.

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens.

Ähnlich wie bei KFold bilden die Testsets von GroupKFold eine vollständige Partition aller Daten.

Während GroupKFold versucht, die gleiche Anzahl von Samples in jedem Fold zu platzieren, wenn shuffle=False ist, versucht es bei shuffle=True, eine gleiche Anzahl von verschiedenen Gruppen in jedem Fold zu platzieren (berücksichtigt aber keine Gruppengrößen).

3.1.2.4.2. StratifiedGroupKFold

StratifiedGroupKFold ist ein Kreuzvalidierungsschema, das sowohl StratifiedKFold als auch GroupKFold kombiniert. Die Idee ist, zu versuchen, die Verteilung der Klassen in jeder Aufteilung beizubehalten, während jede Gruppe innerhalb einer einzigen Aufteilung bleibt. Das kann nützlich sein, wenn Sie einen unausgeglichenen Datensatz haben und die Verwendung von nur GroupKFold zu verzerrten Aufteilungen führen könnte.

Beispiel

>>> from sklearn.model_selection import StratifiedGroupKFold
>>> X = list(range(18))
>>> y = [1] * 6 + [0] * 12
>>> groups = [1, 2, 3, 3, 4, 4, 1, 1, 2, 2, 3, 4, 5, 5, 5, 6, 6, 6]
>>> sgkf = StratifiedGroupKFold(n_splits=3)
>>> for train, test in sgkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[ 0  2  3  4  5  6  7 10 11 15 16 17] [ 1  8  9 12 13 14]
[ 0  1  4  5  6  7  8  9 11 12 13 14] [ 2  3 10 15 16 17]
[ 1  2  3  8  9 10 12 13 14 15 16 17] [ 0  4  5  6  7 11]

Implementierungshinweise

• Mit der aktuellen Implementierung ist in den meisten Szenarien kein vollständiges Mischen möglich. Wenn shuffle=True gesetzt ist, geschieht Folgendes:

  1. Alle Gruppen werden gemischt.

  2. Gruppen werden nach der Standardabweichung der Klassen sortiert, wobei eine stabile Sortierung verwendet wird.

  3. Die sortierten Gruppen werden durchlaufen und den Folds zugewiesen.

  Das bedeutet, dass nur Gruppen mit der gleichen Standardabweichung der Klassenverteilung gemischt werden, was nützlich sein kann, wenn jede Gruppe nur eine einzige Klasse hat.

• Der Algorithmus weist jeder Gruppe gierig einen von n_splits Testdatensätzen zu und wählt den Testdatensatz, der die Varianz der Klassenverteilung über die Testdatensätze minimiert. Die Gruppenzuweisung erfolgt von Gruppen mit höchster zu niedrigster Varianz in der Klassenhäufigkeit, d. h. große Gruppen mit Schwerpunkt auf einer oder wenigen Klassen werden zuerst zugewiesen.

• Diese Aufteilung ist suboptimal in dem Sinne, dass sie unausgeglichene Aufteilungen erzeugen kann, auch wenn eine perfekte Stratifizierung möglich ist. Wenn Sie eine relativ ähnliche Verteilung der Klassen in jeder Gruppe haben, ist die Verwendung von GroupKFold besser.

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens für ungleiche Gruppen

3.1.2.4.3. Leave One Group Out

LeaveOneGroupOut ist ein Kreuzvalidierungsschema, bei dem jeder Split Stichproben enthält, die zu einer bestimmten Gruppe gehören. Gruppeninformationen werden über ein Array bereitgestellt, das die Gruppe jeder Stichprobe kodiert.

Jeder Trainingsdatensatz besteht somit aus allen Stichproben außer denen, die sich auf eine bestimmte Gruppe beziehen. Dies ist dasselbe wie LeavePGroupsOut mit n_groups=1 und dasselbe wie GroupKFold mit n_splits, das gleich der Anzahl der eindeutigen Labels ist, die an den groups-Parameter übergeben wurden.

Zum Beispiel können im Falle mehrerer Experimente LeaveOneGroupOut verwendet werden, um eine Kreuzvalidierung basierend auf den verschiedenen Experimenten zu erstellen: Wir erstellen einen Trainingsdatensatz, der die Stichproben aller Experimente außer einem verwendet.

>>> from sklearn.model_selection import LeaveOneGroupOut

>>> X = [1, 5, 10, 50, 60, 70, 80]
>>> y = [0, 1, 1, 2, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3, 3]
>>> logo = LeaveOneGroupOut()
>>> for train, test in logo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[2 3 4 5 6] [0 1]
[0 1 4 5 6] [2 3]
[0 1 2 3] [4 5 6]

Eine weitere gängige Anwendung ist die Verwendung von Zeitinformationen: Zum Beispiel könnten die Gruppen das Erfassungsjahr der Stichproben sein und somit eine Kreuzvalidierung anhand von zeitbasierten Aufteilungen ermöglichen.

3.1.2.4.4. Leave P Groups Out

LeavePGroupsOut ähnelt LeaveOneGroupOut, entfernt jedoch Stichproben, die sich auf \(P\) Gruppen beziehen, für jeden Trainings-/Testdatensatz. Alle möglichen Kombinationen von \(P\) Gruppen werden weggelassen, was bedeutet, dass sich Testdatensätze für \(P>1\) überschneiden.

Beispiel für Leave-2-Group Out

>>> from sklearn.model_selection import LeavePGroupsOut

>>> X = np.arange(6)
>>> y = [1, 1, 1, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3]
>>> lpgo = LeavePGroupsOut(n_groups=2)
>>> for train, test in lpgo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]

3.1.2.4.5. Group Shuffle Split

Der Iterator GroupShuffleSplit verhält sich als Kombination aus ShuffleSplit und LeavePGroupsOut und generiert eine Sequenz von zufälligen Aufteilungen, bei denen eine Teilmenge von Gruppen für jeden Split zurückgehalten wird. Jede Trainings-/Testaufteilung wird unabhängig durchgeführt, was bedeutet, dass keine garantierte Beziehung zwischen aufeinanderfolgenden Testdatensätzen besteht.

Hier ist ein Anwendungsbeispiel.

>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "a"]
>>> groups = [1, 1, 2, 2, 3, 3, 4, 4]
>>> gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
>>> for train, test in gss.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
...
[0 1 2 3] [4 5 6 7]
[2 3 6 7] [0 1 4 5]
[2 3 4 5] [0 1 6 7]
[4 5 6 7] [0 1 2 3]

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens.

Diese Klasse ist nützlich, wenn das Verhalten von LeavePGroupsOut gewünscht ist, aber die Anzahl der Gruppen groß genug ist, dass die Generierung aller möglichen Aufteilungen mit \(P\) zurückgehaltenen Gruppen prohibitiv teuer wäre. In einem solchen Szenario bietet GroupShuffleSplit eine zufällige Stichprobe (mit Wiederholung) der von LeavePGroupsOut generierten Trainings-/Testaufteilungen.

3.1.2.5. Verwendung von Kreuzvalidierungsiteratoren zum Aufteilen von Trainings- und Testdaten

Die oben genannten Gruppen-Kreuzvalidierungsfunktionen können auch zum direkten Aufteilen eines Datensatzes in Trainings- und Testteilmengen verwendet werden. Beachten Sie, dass die Hilfsfunktion train_test_split eine Wrapper-Funktion um ShuffleSplit ist und daher nur stratifizierte Aufteilungen (unter Verwendung der Klassenlabels) ermöglicht und keine Gruppen berücksichtigen kann.

Um die Trainings- und Testaufteilung durchzuführen, verwenden Sie die Indizes für die Trainings- und Testteilmengen, die vom Generator ausgegeben werden, der von der split()-Methode des Kreuzvalidierungs-Splitters zurückgegeben wird. Zum Beispiel

>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = np.array([0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001])
>>> y = np.array(["a", "b", "b", "b", "c", "c", "c", "a"])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 4, 4])
>>> train_indx, test_indx = next(
...     GroupShuffleSplit(random_state=7).split(X, y, groups)
... )
>>> X_train, X_test, y_train, y_test = \
...     X[train_indx], X[test_indx], y[train_indx], y[test_indx]
>>> X_train.shape, X_test.shape
((6,), (2,))
>>> np.unique(groups[train_indx]), np.unique(groups[test_indx])
(array([1, 2, 4]), array([3]))

3.1.2.6. Kreuzvalidierung von Zeitreihendaten

Zeitreihendaten zeichnen sich durch die Korrelation zwischen Beobachtungen aus, die zeitlich nah beieinander liegen (Autokorrelation). Klassische Kreuzvalidierungstechniken wie KFold und ShuffleSplit gehen jedoch davon aus, dass die Stichproben unabhängig und identisch verteilt sind, und würden zu einer unangemessenen Korrelation zwischen Trainings- und Testinstanzen (was zu schlechten Schätzungen des Generalisierungsfehlers führt) bei Zeitreihendaten führen. Daher ist es sehr wichtig, unser Modell für Zeitreihendaten anhand der "zukünftigen" Beobachtungen zu bewerten, die den Stichproben, die zum Trainieren des Modells verwendet werden, am wenigsten ähneln. Um dies zu erreichen, bietet TimeSeriesSplit eine Lösung.

3.1.2.6.1. Time Series Split

TimeSeriesSplit ist eine Variante von k-fold, die die ersten \(k\) Folds als Trainingsdatensatz und den \((k+1)\)-ten Fold als Testdatensatz zurückgibt. Beachten Sie, dass im Gegensatz zu Standard-Kreuzvalidierungsmethoden aufeinanderfolgende Trainingsdatensätze Obermengen der vorhergehenden sind. Außerdem werden alle überschüssigen Daten zum ersten Trainingspartition hinzugefügt, der immer zum Trainieren des Modells verwendet wird.

Diese Klasse kann zur Kreuzvalidierung von Zeitreihendatenstichproben verwendet werden, die in festen Zeitintervallen beobachtet werden. Tatsächlich müssen die Folds die gleiche Dauer repräsentieren, um vergleichbare Metriken über die Folds hinweg zu haben.

Beispiel für eine 3-Split-Zeitreihen-Kreuzvalidierung auf einem Datensatz mit 6 Stichproben

>>> from sklearn.model_selection import TimeSeriesSplit

>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit(n_splits=3)
>>> print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
>>> for train, test in tscv.split(X):
...     print("%s %s" % (train, test))
[0 1 2] [3]
[0 1 2 3] [4]
[0 1 2 3 4] [5]

Hier ist eine Visualisierung des Kreuzvalidierungsverhaltens.

3.1.3. Ein Hinweis zum Mischen

Wenn die Datenreihenfolge nicht beliebig ist (z. B. Stichproben mit derselben Klassenbezeichnung sind zusammenhängend), kann das vorherige Mischen unerlässlich sein, um ein aussagekräftiges Kreuzvalidierungsergebnis zu erzielen. Das Gegenteil kann jedoch der Fall sein, wenn die Stichproben nicht unabhängig und identisch verteilt sind. Wenn Stichproben beispielsweise Nachrichtenartikel darstellen und nach ihrer Veröffentlichungszeit geordnet sind, führt das Mischen der Daten wahrscheinlich zu einem überangepassten Modell und einem aufgeblähten Validierungs-Score: Es wird auf Stichproben getestet, die künstlich ähnlich (zeitlich nah) zu den Trainingsstichproben sind.

Einige Kreuzvalidierungsiteratoren, wie KFold, haben eine integrierte Option, die Datenindizes vor dem Aufteilen zu mischen. Beachten Sie, dass

• Dies verbraucht weniger Speicher als das Mischen der Daten direkt.

• Standardmäßig findet kein Mischen statt, auch nicht für die (stratifizierte) K-Fold-Kreuzvalidierung, die durch Angabe von cv=some_integer für cross_val_score, Grid Search usw. durchgeführt wird. Beachten Sie, dass train_test_split immer noch eine zufällige Aufteilung zurückgibt.

• Der Parameter random_state ist standardmäßig None, was bedeutet, dass das Mischen jedes Mal anders ist, wenn KFold(..., shuffle=True) iteriert wird. GridSearchCV verwendet jedoch jedes Mal dasselbe Mischen für jeden Parametersatz, der von einem einzelnen Aufruf seiner fit-Methode validiert wird.

• Um identische Ergebnisse für jeden Split zu erhalten, setzen Sie random_state auf eine Ganzzahl.

Weitere Details zur Steuerung der Zufälligkeit von CV-Splittern und zur Vermeidung häufiger Fallstricke finden Sie unter Zufälligkeit steuern.

3.1.4. Kreuzvalidierung und Modellauswahl

Kreuzvalidierungsiteratoren können auch verwendet werden, um direkt eine Modellauswahl mittels Grid Search für die optimalen Hyperparameter des Modells durchzuführen. Dies ist das Thema des nächsten Abschnitts: Hyperparameter eines Schätzers abstimmen.

3.1.5. Permutationstest-Score

permutation_test_score bietet eine weitere Möglichkeit, die Leistung eines Prädiktors zu bewerten. Es liefert einen permutationsbasierten p-Wert, der angibt, wie wahrscheinlich es ist, dass eine beobachtete Leistung des Schätzers durch Zufall erzielt wird. Die Nullhypothese dieses Tests besagt, dass der Schätzer keine statistische Abhängigkeit zwischen den Merkmalen und den Zielvariablen ausnutzt, um korrekte Vorhersagen auf ausgelassenen Daten zu treffen. permutation_test_score generiert eine Nullverteilung, indem n_permutations verschiedene Permutationen der Daten berechnet werden. Bei jeder Permutation werden die Zielwerte zufällig durchgemischt, wodurch jede Abhängigkeit zwischen den Merkmalen und den Zielvariablen beseitigt wird. Der ausgegebene p-Wert ist der Anteil der Permutationen, deren Kreuzvalidierungs-Score besser oder gleich dem wahren Score ohne Permutation der Zielvariablen ist. Für zuverlässige Ergebnisse sollte n_permutations typischerweise größer als 100 und cv zwischen 3 und 10 Folds betragen.

Ein niedriger p-Wert liefert den Beweis dafür, dass der Datensatz eine echte Abhängigkeit zwischen Merkmalen und Zielvariablen enthält und dass der Schätzer diese Abhängigkeit nutzen konnte, um gute Ergebnisse zu erzielen. Ein hoher p-Wert könnte umgekehrt auf eines von beidem zurückzuführen sein:

• ein Mangel an Abhängigkeit zwischen Merkmalen und Zielvariablen (d. h. es gibt keine systematische Beziehung und alle beobachteten Muster sind wahrscheinlich auf Zufall zurückzuführen)

• oder weil der Schätzer die Abhängigkeit in den Daten nicht nutzen konnte (z. B. weil er unterangepasst war).

Im letzteren Fall würde die Verwendung eines besser geeigneten Schätzers, der die Struktur in den Daten nutzen kann, zu einem niedrigeren p-Wert führen.

Kreuzvalidierung liefert Informationen darüber, wie gut ein Schätzer generalisiert, indem sie die Bandbreite seiner erwarteten Scores schätzt. Ein auf einem hochdimensionalen Datensatz ohne Struktur trainierter Schätzer kann jedoch durch Zufall besser abschneiden als erwartet. Dies kann typischerweise bei kleinen Datensätzen mit weniger als einigen hundert Stichproben vorkommen. permutation_test_score liefert Informationen darüber, ob der Schätzer eine reale Abhängigkeit zwischen Merkmalen und Zielvariablen gefunden hat, und kann bei der Bewertung der Leistung des Schätzers helfen.

Es ist wichtig zu beachten, dass dieser Test auch bei nur schwacher Struktur in den Daten niedrige p-Werte erzeugt hat, da in den entsprechenden permutierten Datensätzen absolut keine Struktur vorhanden ist. Dieser Test kann daher nur zeigen, ob das Modell zufälliges Raten zuverlässig übertrifft.

Schließlich wird permutation_test_score im Brute-Force-Verfahren berechnet und passt intern (n_permutations + 1) * n_cv Modelle an. Er ist daher nur für kleine Datensätze handhabbar, bei denen die Anpassung eines einzelnen Modells sehr schnell ist. Die Verwendung des Parameters n_jobs parallelisiert die Berechnung und beschleunigt sie somit.

Beispiele

• Testen der Signifikanz eines Klassifikations-Scores mit Permutationen

Referenzen

• Ojala und Garriga. Permutation Tests for Studying Classifier Performance. J. Mach. Learn. Res. 2010.