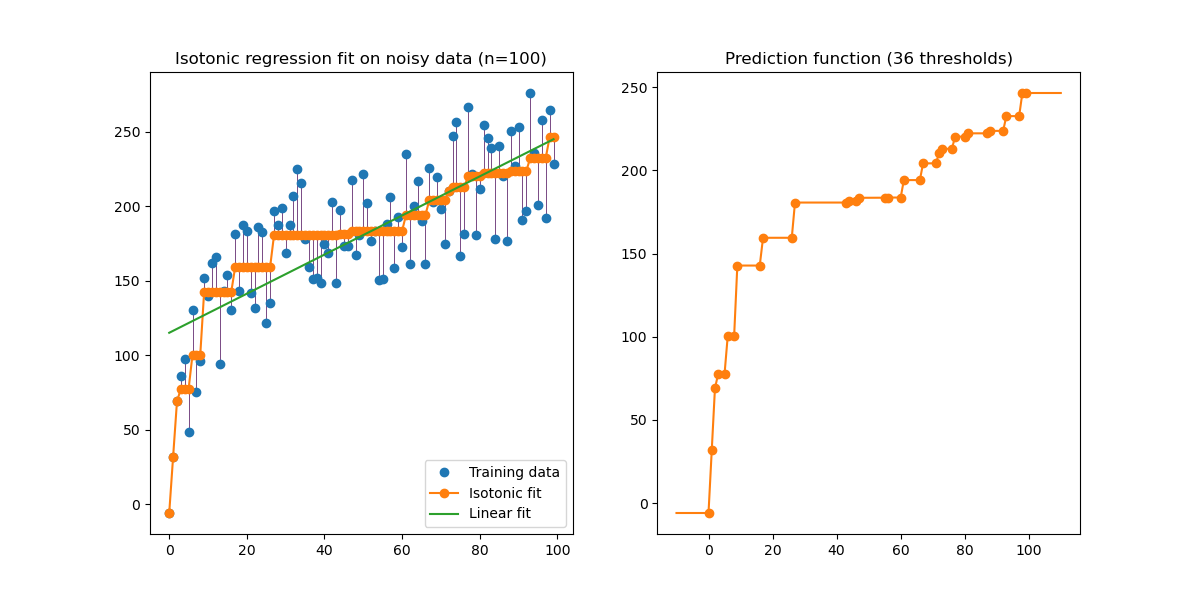
1.15. Isotonische Regression#
Die Klasse IsotonicRegression passt eine nicht abnehmende reelle Funktion an 1D-Daten an. Sie löst das folgende Problem:
unter der Bedingung \(\hat{y}_i \le \hat{y}_j\) wann immer \(X_i \le X_j\), wobei die Gewichte \(w_i\) strikt positiv sind und sowohl X als auch y beliebige reelle Größen sind.
Der Parameter increasing ändert die Bedingung zu \(\hat{y}_i \ge \hat{y}_j\) wann immer \(X_i \le X_j\). Wenn er auf 'auto' gesetzt wird, wählt er automatisch die Bedingung basierend auf Spearmans Rangkorrelationskoeffizient.
IsotonicRegression erzeugt eine Reihe von Vorhersagen \(\hat{y}_i\) für die Trainingsdaten, die im Sinne des mittleren quadratischen Fehlers am nächsten an den Zielwerten \(y\) liegen. Diese Vorhersagen werden für die Vorhersage für ungesehene Daten interpoliert. Die Vorhersagen von IsotonicRegression bilden somit eine stückweise lineare Funktion.
Beispiele