1.2. Lineare und quadratische Diskriminanzanalyse#
Lineare Diskriminanzanalyse (LinearDiscriminantAnalysis) und Quadratische Diskriminanzanalyse (QuadraticDiscriminantAnalysis) sind zwei klassische Klassifikatoren mit, wie ihre Namen schon sagen, einer linearen bzw. einer quadratischen Entscheidungsoberfläche.
Diese Klassifikatoren sind attraktiv, da sie geschlossene Lösungen haben, die einfach berechnet werden können, inhärent multiklass sind, sich in der Praxis gut bewährt haben und keine zu stimmenden Hyperparameter haben.
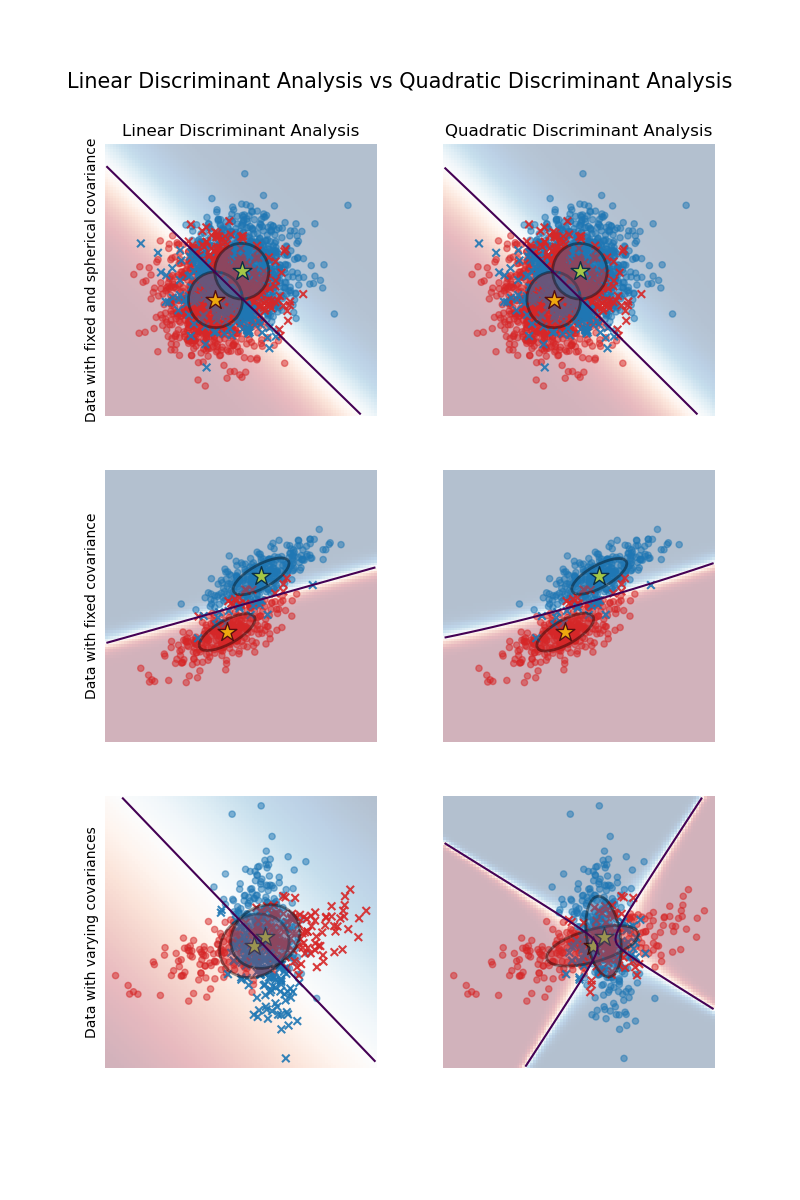
Die Grafik zeigt Entscheidungsgrenzen für die lineare und die quadratische Diskriminanzanalyse. Die untere Reihe zeigt, dass die lineare Diskriminanzanalyse nur lineare Grenzen erlernen kann, während die quadratische Diskriminanzanalyse quadratische Grenzen erlernen kann und daher flexibler ist.
Beispiele
Lineare und quadratische Diskriminanzanalyse mit Kovarianzellipsoid: Vergleich von LDA und QDA auf synthetischen Daten.
1.2.1. Dimensionsreduktion mittels linearer Diskriminanzanalyse#
LinearDiscriminantAnalysis kann zur überwachten Dimensionsreduktion verwendet werden, indem die Eingabedaten auf einen linearen Unterraum projiziert werden, der aus den Richtungen besteht, die die Trennung zwischen den Klassen maximieren (in einem präzisen Sinne, der im nachstehenden mathematischen Abschnitt erläutert wird). Die Dimension des Ausgaberaums ist notwendigerweise kleiner als die Anzahl der Klassen, daher handelt es sich im Allgemeinen um eine eher starke Dimensionsreduktion, die nur in einem multiklass-Setting sinnvoll ist.
Dies ist in der transform-Methode implementiert. Die gewünschte Dimensionalität kann mit dem Parameter n_components eingestellt werden. Dieser Parameter hat keinen Einfluss auf die Methoden fit und predict.
Beispiele
Vergleich von LDA und PCA 2D-Projektion des Iris-Datensatzes: Vergleich von LDA und PCA zur Dimensionsreduktion des Iris-Datensatzes.
1.2.2. Mathematische Formulierung der LDA- und QDA-Klassifikatoren#
Sowohl LDA als auch QDA können aus einfachen probabilistischen Modellen abgeleitet werden, die die klassenbedingte Verteilung der Daten \(P(X|y=k)\) für jede Klasse \(k\) modellieren. Vorhersagen können dann mithilfe der Bayes'schen Regel für jede Trainingsprobe \(x \in \mathbb{R}^d\) erhalten werden.
und wir wählen die Klasse \(k\), die diese Posterior-Wahrscheinlichkeit maximiert.
Genauer gesagt wird für die lineare und quadratische Diskriminanzanalyse \(P(x|y)\) als multivariate Gaußsche Verteilung mit der Dichte
modelliert, wobei \(d\) die Anzahl der Merkmale ist.
1.2.2.1. QDA#
Gemäß dem obigen Modell ist der Logarithmus des Posteriors
wobei der konstante Term \(Cst\) dem Nenner \(P(x)\) entspricht, zusätzlich zu anderen konstanten Termen aus der Gaußschen Verteilung. Die vorhergesagte Klasse ist diejenige, die diesen Log-Posterior maximiert.
Hinweis
Beziehung zu Gaussian Naive Bayes
Wenn im QDA-Modell angenommen wird, dass die Kovarianzmatrizen diagonal sind, dann wird angenommen, dass die Eingaben in jeder Klasse bedingt unabhängig sind, und der resultierende Klassifikator ist äquivalent zum Gaussian Naive Bayes-Klassifikator naive_bayes.GaussianNB.
1.2.2.2. LDA#
LDA ist ein Spezialfall von QDA, bei dem angenommen wird, dass die Gaußschen Verteilungen für jede Klasse die gleiche Kovarianzmatrix teilen: \(\Sigma_k = \Sigma\) für alle \(k\). Dies reduziert den Log-Posterior auf
Der Term \((x-\mu_k)^T \Sigma^{-1} (x-\mu_k)\) entspricht der Mahalanobis-Distanz zwischen der Probe \(x\) und dem Mittelwert \(\mu_k\). Die Mahalanobis-Distanz gibt an, wie nah \(x\) an \(\mu_k\) liegt, und berücksichtigt dabei auch die Varianz jedes Merkmals. Wir können LDA somit interpretieren als die Zuordnung von \(x\) zur Klasse, deren Mittelwert in Bezug auf die Mahalanobis-Distanz am nächsten liegt, unter Berücksichtigung der A-priori-Wahrscheinlichkeiten der Klassen.
Der Log-Posterior von LDA kann auch wie folgt geschrieben werden [3]:
wobei \(\omega_k = \Sigma^{-1} \mu_k\) und \(\omega_{k0} = -\frac{1}{2} \mu_k^T\Sigma^{-1}\mu_k + \log P (y = k)\). Diese Größen entsprechen den Attributen coef_ bzw. intercept_.
Aus der obigen Formel ist klar ersichtlich, dass LDA eine lineare Entscheidungsoberfläche hat. Im Fall von QDA gibt es keine Annahmen über die Kovarianzmatrizen \(\Sigma_k\) der Gaußschen Verteilungen, was zu quadratischen Entscheidungsoberflächen führt. Weitere Details finden Sie in [1].
1.2.3. Mathematische Formulierung der LDA-Dimensionsreduktion#
Zuerst sei angemerkt, dass die K Mittelwerte \(\mu_k\) Vektoren in \(\mathbb{R}^d\) sind und in einem affinen Unterraum \(H\) der Dimension höchstens \(K - 1\) liegen (2 Punkte liegen auf einer Linie, 3 Punkte auf einer Ebene usw.).
Wie oben erwähnt, können wir LDA so interpretieren, dass \(x\) der Klasse zugeordnet wird, deren Mittelwert \(\mu_k\) in Bezug auf die Mahalanobis-Distanz am nächsten liegt, unter Berücksichtigung der A-priori-Wahrscheinlichkeiten der Klassen. Alternativ ist LDA äquivalent dazu, die Daten zuerst zu *sphärisieren*, so dass die Kovarianzmatrix die Identität ist, und dann \(x\) dem nächstgelegenen Mittelwert in Bezug auf die euklidische Distanz zuzuordnen (immer noch unter Berücksichtigung der Klassen-A-priori-Wahrscheinlichkeiten).
Die Berechnung der euklidischen Distanzen in diesem d-dimensionalen Raum ist äquivalent zur ersten Projektion der Datenpunkte auf \(H\) und zur Berechnung der Distanzen dort (da die anderen Dimensionen in Bezug auf die Distanz zu jeder Klasse gleich beitragen). Anders ausgedrückt: Wenn \(x\) im ursprünglichen Raum am nächsten zu \(\mu_k\) liegt, gilt dies auch in \(H\). Dies zeigt, dass implizit im LDA-Klassifikator eine Dimensionsreduktion durch lineare Projektion auf einen \(K-1\)-dimensionalen Raum stattfindet.
Wir können die Dimension noch weiter auf ein gewähltes \(L\) reduzieren, indem wir auf den linearen Unterraum \(H_L\) projizieren, der die Varianz der \(\mu^*_k\) nach der Projektion maximiert (im Wesentlichen führen wir eine Art PCA für die transformierten Klassenmittelwerte \(\mu^*_k\) durch). Dieses \(L\) entspricht dem Parameter n_components, der in der Methode transform verwendet wird. Weitere Details finden Sie in [1].
1.2.4. Schrumpfung und Kovarianzschätzer#
Schrumpfung ist eine Form der Regularisierung, die verwendet wird, um die Schätzung von Kovarianzmatrizen zu verbessern, wenn die Anzahl der Trainingsstichproben im Vergleich zur Anzahl der Merkmale gering ist. In diesem Szenario ist die empirische Stichprobenkovarianz ein schlechter Schätzer, und die Schrumpfung hilft, die Generalisierungsleistung des Klassifikators zu verbessern. Schrumpfung kann mit LDA (oder QDA) verwendet werden, indem der Parameter shrinkage der Klasse LinearDiscriminantAnalysis (oder QuadraticDiscriminantAnalysis) auf 'auto' gesetzt wird. Dies bestimmt automatisch den optimalen Schrumpfungsparameter analytisch nach dem von Ledoit und Wolf eingeführten Lemma [2]. Beachten Sie, dass die Schrumpfung derzeit nur funktioniert, wenn der Parameter solver auf 'lsqr' oder 'eigen' gesetzt ist (nur 'eigen' ist für QDA implementiert).
Der Parameter shrinkage kann auch manuell zwischen 0 und 1 eingestellt werden. Insbesondere entspricht ein Wert von 0 keiner Schrumpfung (was bedeutet, dass die empirische Kovarianzmatrix verwendet wird) und ein Wert von 1 entspricht vollständiger Schrumpfung (was bedeutet, dass die Diagonalmatrix der Varianzen als Schätzung für die Kovarianzmatrix verwendet wird). Das Setzen dieses Parameters auf einen Wert zwischen diesen beiden Extremen schätzt eine geschrumpfte Version der Kovarianzmatrix.
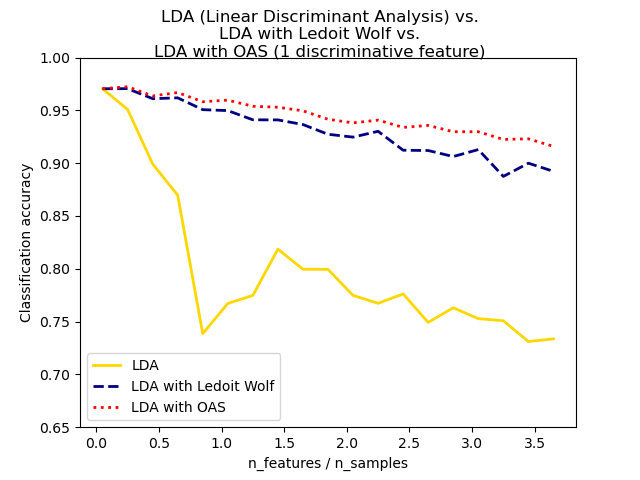
Der geschrumpfte Ledoit-Wolf-Schätzer für die Kovarianz ist möglicherweise nicht immer die beste Wahl. Wenn beispielsweise die Daten normalverteilt sind, liefert der Oracle Approximating Shrinkage-Schätzer sklearn.covariance.OAS einen kleineren mittleren quadratischen Fehler als die Ledoit-Wolf-Formel bei Verwendung von shrinkage="auto". Bei LDA und QDA wird angenommen, dass die Daten bedingt auf die Klasse Gaußverteilt sind. Wenn diese Annahmen zutreffen, erzielen LDA und QDA mit dem OAS-Schätzer für die Kovarianz eine höhere Klassifikationsgenauigkeit als mit Ledoit-Wolf oder dem empirischen Kovarianzschätzer.
Der Kovarianzschätzer kann über den Parameter covariance_estimator der Klassen discriminant_analysis.LinearDiscriminantAnalysis und discriminant_analysis.QuadraticDiscriminantAnalysis ausgewählt werden. Ein Kovarianzschätzer sollte eine fit-Methode und ein Attribut covariance_ wie alle Kovarianzschätzer im Modul sklearn.covariance haben.
Beispiele
Normale, Ledoit-Wolf und OAS lineare Diskriminanzanalyse zur Klassifikation: Vergleich von LDA-Klassifikatoren mit empirischem, Ledoit-Wolf und OAS-Kovarianzschätzer.
1.2.5. Schätzalgorithmen#
Die Verwendung von LDA und QDA erfordert die Berechnung des Log-Posteriors, der von den Klassen-A-priori-Wahrscheinlichkeiten \(P(y=k)\), den Klassenmittelwerten \(\mu_k\) und den Kovarianzmatrizen abhängt.
Der Solver 'svd' ist der Standard-Solver für LinearDiscriminantAnalysis und QuadraticDiscriminantAnalysis. Er kann sowohl Klassifizierung als auch Transformation (für LDA) durchführen. Da er nicht auf die Berechnung der Kovarianzmatrix angewiesen ist, kann der 'svd'-Solver in Situationen bevorzugt werden, in denen die Anzahl der Merkmale groß ist. Der 'svd'-Solver kann nicht mit Schrumpfung verwendet werden. Für QDA beruht die Verwendung des SVD-Solvers auf der Tatsache, dass die Kovarianzmatrix \(\Sigma_k\) definitionsgemäß gleich \(\frac{1}{n - 1} X_k^TX_k = \frac{1}{n - 1} V S^2 V^T\) ist, wobei \(V\) aus der SVD der (zentrierten) Matrix stammt: \(X_k = U S V^T\). Es stellt sich heraus, dass wir den obigen Log-Posterior berechnen können, ohne \(\Sigma\) explizit berechnen zu müssen: Die Berechnung von \(S\) und \(V\) mittels der SVD von \(X\) reicht aus. Für LDA werden zwei SVDs berechnet: die SVD der zentrierten Eingabematrix \(X\) und die SVD der klassenweisen Mittelwertvektoren.
Der Solver 'lsqr' ist ein effizienter Algorithmus, der nur für die Klassifizierung funktioniert. Er muss die Kovarianzmatrix \(\Sigma\) explizit berechnen und unterstützt Schrumpfung und benutzerdefinierte Kovarianzschätzer. Dieser Solver berechnet die Koeffizienten \(\omega_k = \Sigma^{-1}\mu_k\) durch Lösen von \(\Sigma \omega = \mu_k\) und vermeidet somit die explizite Berechnung der Inversen \(\Sigma^{-1}\).
Der Solver 'eigen' für LinearDiscriminantAnalysis basiert auf der Optimierung des Verhältnisses von Streuung zwischen den Klassen zu Streuung innerhalb der Klassen. Er kann sowohl für Klassifizierung als auch für Transformation verwendet werden und unterstützt Schrumpfung. Für QuadraticDiscriminantAnalysis basiert der Solver 'eigen' auf der Berechnung der Eigenwerte und Eigenvektoren der Kovarianzmatrix jeder Klasse. Er ermöglicht die Verwendung von Schrumpfung für die Klassifizierung. Der Solver 'eigen' muss jedoch die Kovarianzmatrix berechnen, sodass er für Situationen mit einer großen Anzahl von Merkmalen möglicherweise nicht geeignet ist.
Referenzen