make_classification#
- sklearn.datasets.make_classification(n_samples=100, n_features=20, *, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None, return_X_y=True)[Quelle]#
Generiert eine zufällige Klassifikationsaufgabe mit n Klassen.
Erstellt zunächst Cluster von Punkten, die normalverteilt sind (Std=1) um die Eckpunkte eines
n_informative-dimensionalen Hyperwürfels mit Seitenlängen2*class_sepund weist jeder Klasse eine gleiche Anzahl von Clustern zu. Es wird eine Abhängigkeit zwischen diesen Merkmalen eingeführt und verschiedene Arten von zusätzlichem Rauschen zu den Daten hinzugefügt.Ohne Mischen werden die Merkmale
Xhorizontal in folgender Reihenfolge gestapelt: die primärenn_informativeMerkmale, gefolgt vonn_redundantlinearen Kombinationen der informativen Merkmale, gefolgt vonn_repeatedDuplikaten, die zufällig mit Zurücklegen aus den informativen und redundanten Merkmalen gezogen werden. Die verbleibenden Merkmale werden mit zufälligem Rauschen gefüllt. Daher sind ohne Mischen alle nützlichen Merkmale in den SpaltenX[:, :n_informative + n_redundant + n_repeated]enthalten.Lesen Sie mehr im Benutzerhandbuch.
- Parameter:
- n_samplesint, Standard=100
Die Anzahl der Stichproben.
- n_featuresint, Standard=20
Die Gesamtzahl der Merkmale. Diese umfassen
n_informativeinformative Merkmale,n_redundantredundante Merkmale,n_repeatedduplizierte Merkmale undn_features-n_informative-n_redundant-n_repeatednutzlose Merkmale, die zufällig gezogen werden.- n_informativeint, Standard=2
Die Anzahl der informativen Merkmale. Jede Klasse besteht aus einer Anzahl von Gauß-Clustern, die jeweils um die Eckpunkte eines Hyperwürfels in einem Unterraum der Dimension
n_informativeangeordnet sind. Für jeden Cluster werden informative Merkmale unabhängig von N(0, 1) gezogen und dann zufällig linear innerhalb jedes Clusters kombiniert, um Kovarianz hinzuzufügen. Die Cluster werden dann auf die Eckpunkte des Hyperwürfels gesetzt.- n_redundantint, Standard=2
Die Anzahl der redundanten Merkmale. Diese Merkmale werden als zufällige lineare Kombinationen der informativen Merkmale generiert.
- n_repeatedint, Standard=0
Die Anzahl der duplizierten Merkmale, die zufällig aus den informativen und den redundanten Merkmalen gezogen werden.
- n_classesint, Standard=2
Die Anzahl der Klassen (oder Labels) des Klassifikationsproblems.
- n_clusters_per_classint, Standard=2
Die Anzahl der Cluster pro Klasse.
- weightsarray-like der Form (n_classes,) oder (n_classes - 1,), Standard=None
Die Anteile der Stichproben, die jeder Klasse zugeordnet werden. Wenn None, dann sind die Klassen ausgewogen. Beachten Sie, dass, wenn
len(weights) == n_classes - 1, das letzte Klassen-Gewicht automatisch abgeleitet wird. Es können mehr alsn_samplesStichproben zurückgegeben werden, wenn die Summe derweights1 überschreitet. Beachten Sie, dass die tatsächlichen Klassenanteile nicht exakt mitweightsübereinstimmen, wennflip_ynicht 0 ist.- flip_yfloat, Standard=0.01
Der Anteil der Stichproben, deren Klasse zufällig zugewiesen wird. Größere Werte fügen Rauschen zu den Labels hinzu und erschweren die Klassifikationsaufgabe. Beachten Sie, dass die Standardeinstellung flip_y > 0 in einigen Fällen zu weniger als
n_classesin y führen kann.- class_sepfloat, Standard=1.0
Der Faktor, der die Größe des Hyperwürfels multipliziert. Größere Werte verteilen die Cluster/Klassen weiter und erleichtern die Klassifikationsaufgabe.
- hypercubebool, Standard=True
Wenn True, werden die Cluster auf die Eckpunkte eines Hyperwürfels gelegt. Wenn False, werden die Cluster auf die Eckpunkte eines zufälligen Polyeders gelegt.
- shiftfloat, ndarray der Form (n_features,) oder None, Standard=0.0
Verschieben Sie die Merkmale um den angegebenen Wert. Wenn None, werden die Merkmale um einen zufälligen Wert in [-class_sep, class_sep] verschoben.
- scalefloat, ndarray der Form (n_features,) oder None, Standard=1.0
Multiplizieren Sie die Merkmale mit dem angegebenen Wert. Wenn None, werden die Merkmale mit einem zufälligen Wert in [1, 100] skaliert. Beachten Sie, dass die Skalierung nach dem Verschieben erfolgt.
- shufflebool, Standard=True
Mischen Sie die Stichproben und die Merkmale.
- random_stateint, RandomState-Instanz oder None, default=None
Bestimmt die Zufallszahlengenerierung für die Datenerstellung. Übergeben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe hinweg. Siehe Glossar.
- return_X_ybool, Standard=True
Wenn True, wird ein Tupel
(X, y)anstelle eines Bunch-Objekts zurückgegeben.Hinzugefügt in Version 1.7.
- Gibt zurück:
- data
Bunchwennreturn_X_yFalseist. Dictionary-ähnliches Objekt mit den folgenden Attributen.
- DESCRstr
Eine Beschreibung der Funktion, die den Datensatz generiert hat.
- parameterdict
Ein Wörterbuch, das die Werte der an die Generatorfunktion übergebenen Argumente speichert.
- feature_infoListe der Länge (n_features)
Eine Beschreibung für jedes generierte Merkmal.
- Xndarray der Form (n_samples, n_features)
Die generierten Samples.
- yndarray der Form (n_samples,)
Ein ganzzahliger Label für die Klassenmitgliedschaft jeder Stichprobe.
Hinzugefügt in Version 1.7.
- (X, y)Tupel, wenn
return_X_yTrue ist Ein Tupel aus generierten Stichproben und Labels.
- data
Siehe auch
make_blobsVereinfachte Variante.
make_multilabel_classificationNicht verwandter Generator für Multilabel-Aufgaben.
Anmerkungen
Der Algorithmus ist von Guyon [1] adaptiert und wurde entwickelt, um den "Madelon"-Datensatz zu generieren.
Referenzen
[1]I. Guyon, „Design of experiments for the NIPS 2003 variable selection benchmark“, 2003.
Beispiele
>>> from sklearn.datasets import make_classification >>> X, y = make_classification(random_state=42) >>> X.shape (100, 20) >>> y.shape (100,) >>> list(y[:5]) [np.int64(0), np.int64(0), np.int64(1), np.int64(1), np.int64(0)]
Galeriebeispiele#
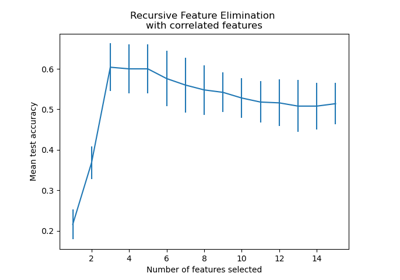
Rekursive Merkmalseliminierung mit Kreuzvalidierung

Leistung eines Klassifikators mit Konfusionsmatrix bewerten
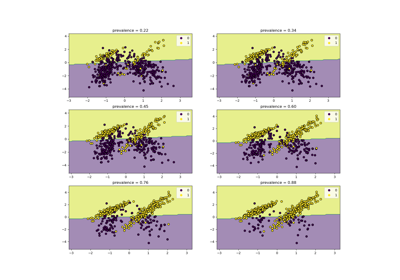
Klassen-Likelihood-Verhältnisse zur Messung der Klassifikationsleistung

Vergleich zwischen Gitter-Suche und sukzessiver Halbierung

Variierende Regularisierung im Multi-Layer Perceptron

Skalierung des Regularisierungsparameters für SVCs